JavaScript實現樹結構(一)
阿新 • • 發佈:2020-03-09
## JavaScript實現樹結構(一)
### 一、樹結構簡介
#### 1.1.簡單瞭解樹結構
**什麼是樹?**
真實的樹:

**樹的特點:**
* 樹一般都有一個**根**,連線著根的是**樹幹**;
* 樹幹會發生分叉,形成許多**樹枝**,樹枝會繼續分化成更小的**樹枝**;
* 樹枝的最後是**葉子**;
現實生活中很多結構都是樹的抽象,模擬的樹結構相當於旋轉`180°`的樹。
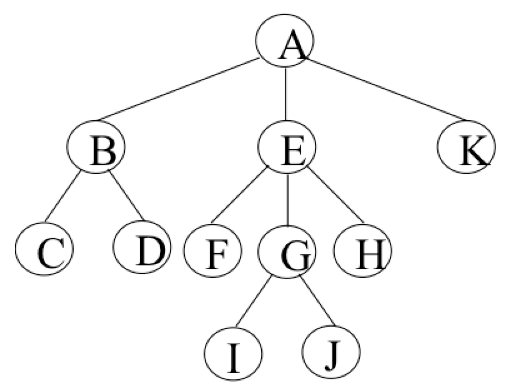
**樹結構對比於陣列/連結串列/雜湊表有哪些優勢呢:**
**陣列:**
* 優點:可以通過**下標值訪問**,效率高;
* 缺點:查詢資料時需要先對資料進行**排序**,生成**有序陣列**,才能提高查詢效率;並且在插入和刪除元素時,需要大量的**位移操作**;
**連結串列:**
* 優點:資料的插入和刪除操作效率都很高;
* 缺點:**查詢**效率低,需要從頭開始依次查詢,直到找到目標資料為止;當需要在連結串列中間位置插入或刪除資料時,插入或刪除的效率都不高。
**雜湊表:**
* 優點:雜湊表的插入/查詢/刪除效率都非常高;
* 缺點:**空間利用率不高**,底層使用的陣列中很多單元沒有被利用;並且雜湊表中的元素是**無序**的,不能按照固定順序遍歷雜湊表中的元素;而且不能快速找出雜湊表中**最大值或最小值**這些特殊值。
**樹結構:**
優點:樹結構綜合了上述三種結構的優點,同時也彌補了它們存在的缺點(雖然效率不一定都比它們高),比如樹結構中資料都是有序的,查詢效率高;空間利用率高;並且可以快速獲取最大值和最小值等。
總的來說:**每種資料結構都有自己特定的應用場景**
**樹結構:**
* **樹(Tree)**:由 n(n ≥ 0)個節點構成的**有限集合**。當 n = 0 時,稱為**空樹**。
對於任一棵非空樹(n > 0),它具備以下性質:
* 數中有一個稱為**根(Root)**的特殊節點,用 **r **表示;
* 其餘節點可分為 m(m > 0)個互不相交的有限集合 T~1~,T~2~,...,T~m~,其中每個集合本身又是一棵樹,稱為原來樹的**子樹(SubTree)**。
**樹的常用術語:**
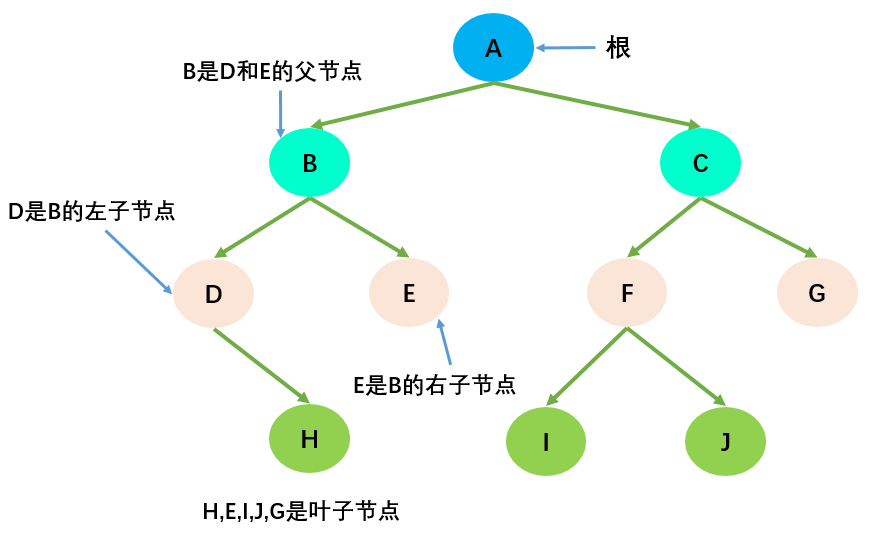
* **節點的度(Degree)**:節點的**子樹個數**,比如節點B的度為2;
* **樹的度**:樹的所有節點中**最大的度數**,如上圖樹的度為2;
* **葉節點(Leaf)**:**度為0的節點**(也稱為葉子節點),如上圖的H,I等;
* **父節點(Parent)**:度不為0的節點稱為父節點,如上圖節點B是節點D和E的父節點;
* **子節點(Child)**:若B是D的父節點,那麼D就是B的子節點;
* **兄弟節點(Sibling)**:具有同一父節點的各節點彼此是兄弟節點,比如上圖的B和C,D和E互為兄弟節點;
* **路徑和路徑長度**:路徑指的是一個節點到另一節點的通道,路徑所包含邊的個數稱為路徑長度,比如A->H的路徑長度為3;
* **節點的層次(Level)**:規定**根節點在1層**,其他任一節點的層數是其父節點的**層數加1**。如B和C節點的層次為2;
* **樹的深度(Depth)**:樹種所有節點中的**最大層次**是這棵樹的深度,如上圖樹的深度為4;
#### 1.2.樹結構的表示方式
* **最普通的表示方法**:
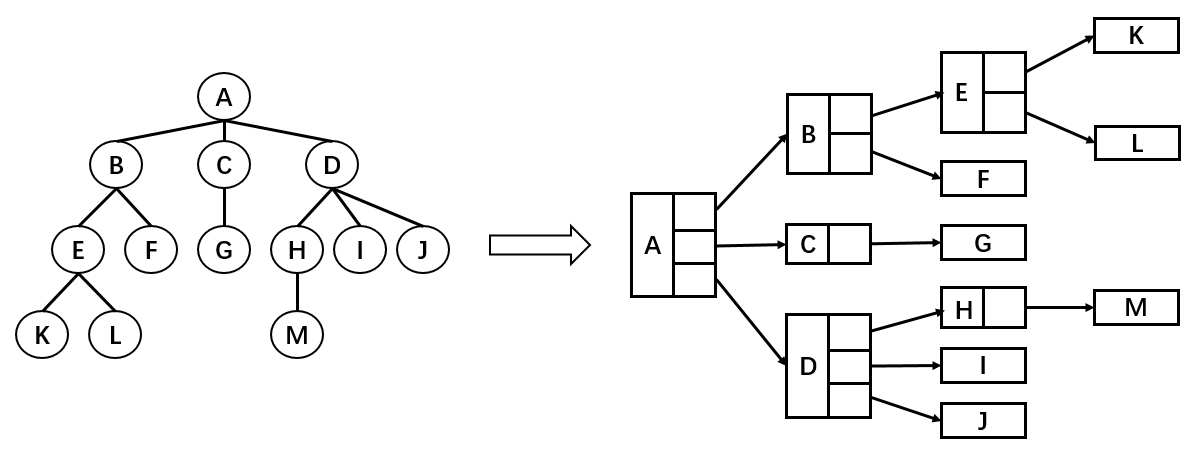
如圖,樹結構的組成方式類似於連結串列,都是由一個個節點連線構成。不過,根據每個父節點子節點數量的不同,每一個父節點需要的引用數量也不同。比如節點A需要3個引用,分別指向子節點B,C,D;B節點需要2個引用,分別指向子節點E和F;K節點由於沒有子節點,所以不需要引用。
這種方法缺點在於我們無法確定某一結點的引用數。
* **兒子-兄弟表示法**:
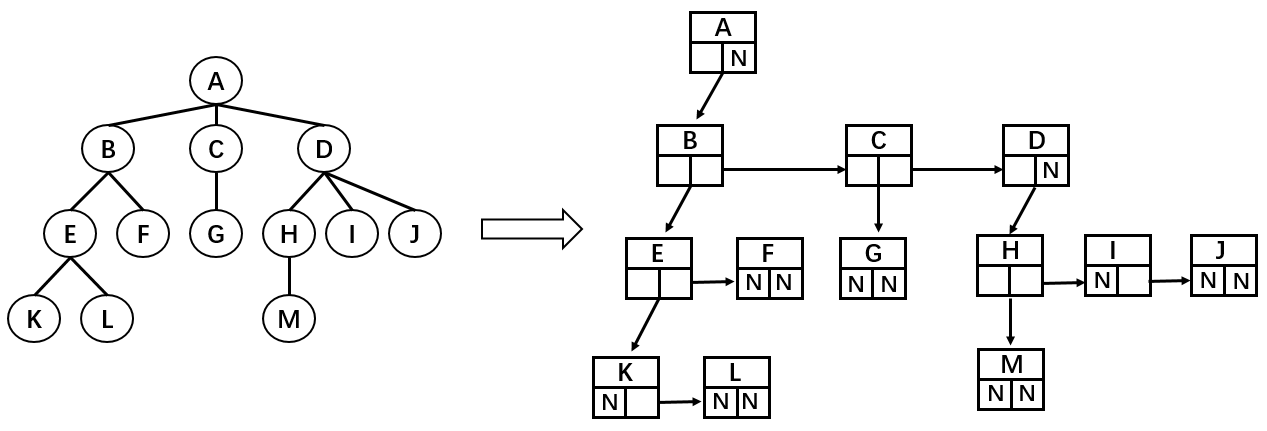
這種表示方法可以完整地記錄每個節點的資料,比如:
```
//節點A
Node{
//儲存資料
this.data = data
//統一隻記錄左邊的子節點
this.leftChild = B
//統一隻記錄右邊的第一個兄弟節點
this.rightSibling = null
}
//節點B
Node{
this.data = data
this.leftChild = E
this.rightSibling = C
}
//節點F
Node{
this.data = data
this.leftChild = null
this.rightSibling = null
}
```
這種表示法的優點在於每一個節點中引用的數量都是確定的。
* **兒子-兄弟表示法旋轉**
以下為兒子-兄弟表示法組成的樹結構:
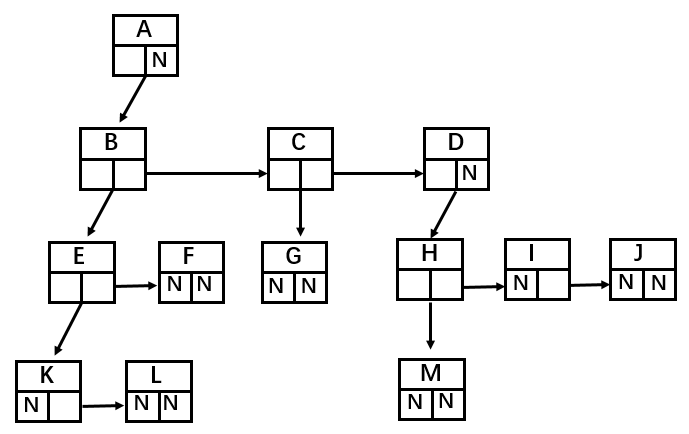
將其順時針旋轉45°之後:
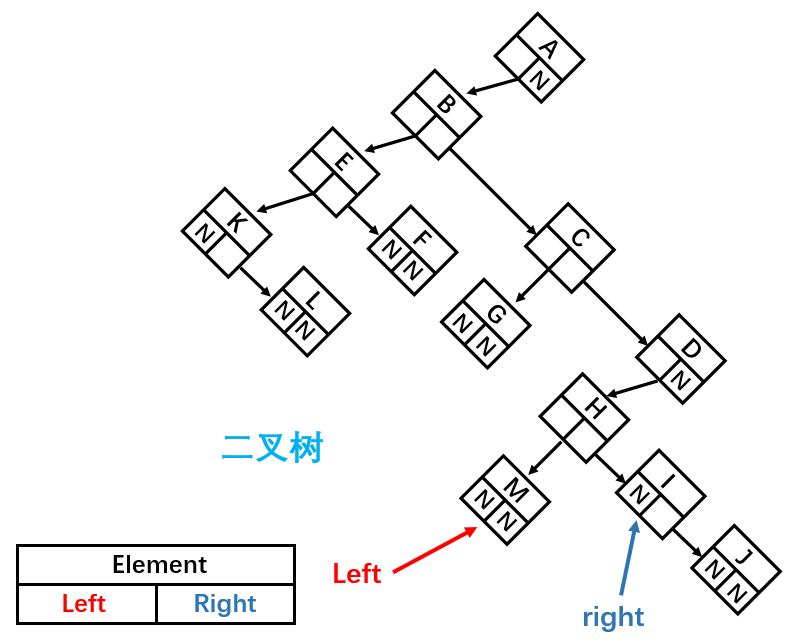
這樣就成為了一棵**二叉樹**,由此我們可以得出結論:**任何樹都可以通過二叉樹進行模擬**。但是這樣父節點不是變了嗎?其實,父節點的設定只是為了方便指向子節點,在程式碼實現中誰是父節點並沒有關係,只要能正確找到對應節點即可。
### 二、二叉樹
#### 2.1.二叉樹簡介
**二叉樹的概念**:如果樹中的每一個節點最多隻能由**兩個子節點**,這樣的樹就稱為**二叉樹**;
二叉樹十分重要,不僅僅是因為簡單,更是因為幾乎所有的樹都可以表示成二叉樹形式。
**二叉樹的組成**:
* 二叉樹可以為空,也就是沒有節點;
* 若二叉樹不為空,則它由根節點和稱為其左子樹TL和右子樹TR的兩個不相交的二叉樹組成;
**二叉樹的五種形態**:
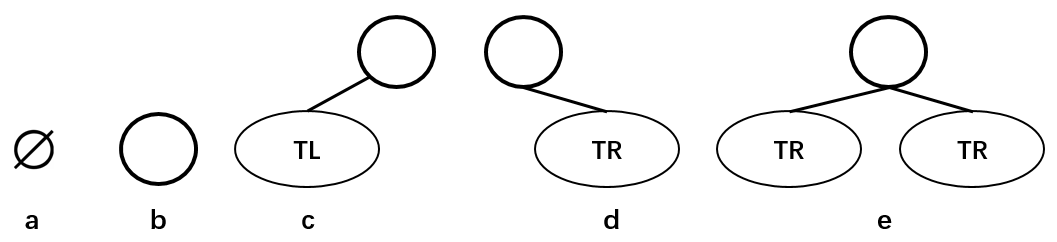
上圖分別表示:空的二叉樹、只有一個節點的二叉樹、只有左子樹TL的二叉樹、只有右子樹TR的二叉樹和有左右兩個子樹的二叉樹。
**二叉樹的特性**:
* 一個二叉樹的第 i 層的最大節點樹為:2^(i-1)^,i >= 1;
* 深度為k的二叉樹的最大節點總數為:2^k^ - 1 ,k >= 1;
* 對任何非空二叉樹,若 n~0~ 表示葉子節點的個數,n~2~表示度為2的非葉子節點個數,那麼兩者滿足關係:n~0~ = n~2~ + 1;如下圖所示:H,E,I,J,G為葉子節點,總數為5;A,B,C,F為度為2的非葉子節點,總數為4;滿足n~0~ = n~2~ + 1的規律。
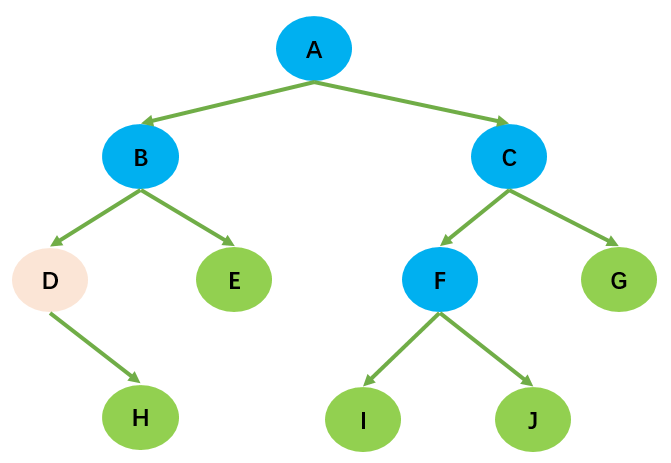
#### 2.2.特殊的二叉樹
**完美二叉樹**
完美二叉樹(Perfect Binary Tree)也成為滿二叉樹(Full Binary Tree),在二叉樹中,除了最下一層的葉子節點外,每層節點都有2個子節點,這就構成了完美二叉樹。

**完全二叉樹**
完全二叉樹(Complete Binary Tree):
* 除了二叉樹最後一層外,其他各層的節點數都達到了最大值;
* 並且,最後一層的葉子節點從左向右是連續存在,只缺失右側若干葉子節點;
* 完美二叉樹是特殊的完全二叉樹;

在上圖中,由於H缺失了右子節點,所以它不是完全二叉樹。
#### 2.3.二叉樹的資料儲存
常見的二叉樹儲存方式為**陣列**和**連結串列**:
**使用陣列:**
* **完全二叉樹**:按從上到下,從左到右的方式儲存資料。

| 節點 | A | B | C | D | E | F | G | H |
| -------- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- |
| **序號** | **1** | **2** | **3** | **4** | **5** | **6** | **7** | **8** |
使用陣列儲存時,取資料的時候也十分方便:左子節點的序號等於父節點序號 * 2,右子節點的序號等於父節點序號 * 2 + 1 。
* **非完全二叉樹**:非完全二叉樹需要轉換成完全二叉樹才能按照上面的方案儲存,這樣會浪費很大的儲存空間。

| 節點 | A | B | C | ^ | ^ | F | ^ | ^ | ^ | ^ | ^ | ^ | M |
| -------- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ------ | ------ | ------ | ------ |
| **序號** | **1** | **2** | **3** | **4** | **5** | **6** | **7** | **8** | **9** | **10** | **11** | **12** | **13** |
**使用連結串列**
二叉樹最常見的儲存方式為**連結串列**:每一個節點封裝成一個Node,Node中包含儲存的資料、左節點的引用和右節點的引用。

### 三、二叉搜尋樹
#### 3.1.認識二叉搜尋樹
**二叉搜尋樹**(**BST**,Binary Search Tree),也稱為**二叉排序樹**和**二叉查詢樹**。
二叉搜尋樹是一棵二叉樹,可以為空;
如果不為空,則滿足以下**性質**:
* 條件1:非空左子樹的**所有**鍵值**小於**其根節點的鍵值。比如三中節點6的所有非空左子樹的鍵值都小於6;
* 條件2:非空右子樹的**所有**鍵值**大於**其根節點的鍵值;比如三中節點6的所有非空右子樹的鍵值都大於6;
* 條件3:左、右子樹本身也都是二叉搜尋樹;

如上圖所示,樹二和樹三符合3個條件屬於二叉樹,樹一不滿足條件3所以不是二叉樹。
**總結:**二叉搜尋樹的特點主要是**較小的值**總是儲存在**左節點**上,相對**較大的值**總是儲存在**右節點**上。這種特點使得二叉搜尋樹的查詢效率非常高,這也就是二叉搜尋樹中"搜尋"的來源。
#### 3.2.二叉搜尋樹應用舉例
下面是一個二叉搜尋樹:

若想在其中查詢資料10,只需要查詢4次,查詢效率非常高。
* 第1次:將10與根節點9進行比較,由於10 > 9,所以10下一步與根節點9的右子節點13比較;
* 第2次:由於10 < 13,所以10下一步與父節點13的左子節點11比較;
* 第3次:由於10 < 11,所以10下一步與父節點11的左子節點10比較;
* 第4次:由於10 = 10,最終查詢到資料10 。
同樣是15個數據,在排序好的陣列中查詢資料10,需要查詢10次:

其實:如果是排序好的陣列,可以通過二分查詢:第一次找9,第二次找13,第三次找15...。我們發現如果把每次二分的資料拿出來以樹的形式表示的話就是**二叉搜尋樹**。這就是陣列二分法查詢效率之所以高的原因。
>
