在工程中有時候需要用到隨機數函式來模擬一些情況，例如加密系統的金鑰來源可以用隨機數函式獲取。

一般來說隨機數函式需要有以下性質：

1：隨機性，不存在統計學偏差，是完全散亂的數列。

2：不可預測性：不能從過去的的數列推算出下一個出現的數

3：不可重現性：除非數列儲存下來，否則不能重新相同的數列（比較難）。

根據以上三個性質，可以將隨機數函式分為“弱偽隨機數”，“強偽隨機數”，“真隨機數”。

其中“真隨機數”靠軟體無法實現，需要藉助物理性質，如量子金鑰更具量子的偏振等物理狀態生成的位元資料即真隨機數，而生成隨機數的裝置稱為“隨機數生成器”。而“偽隨機數”可以依靠軟體來實現，該軟體一般統稱為“偽隨機數生成器”。

本章主要圍繞偽隨機數進行敘述和論證。

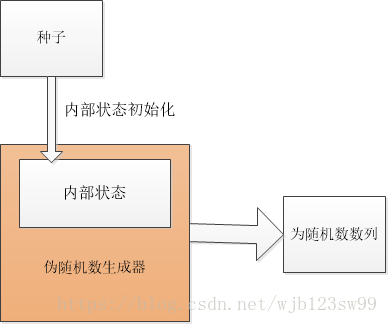
偽隨機數生成器，其結構為

例如下列以系統時間為種子實現內部初始化的偽隨機數生成器，該函式在stdlib.h中提供。

/*******************************************************************************
* Function Name  : QKSGenrnd
* Description    : 生成隨機字串
* Input          ：len: 隨機字串長度
* Output         : buff: 容器
* Return         : None
*******************************************************************************/
void QKSGenrnd(char *buff, int len)
{
	char metachar[] = "QAZWSXEDCRFVTGBYHNUJMIKLOPqazwsxedcrfvtgbyhnujmikolp1234567890";
	int num = sizeof(metachar)-1;

	memset(buff, 0, sizeof(buff));
	srand(time(NULL)); //隨機數函式初始化，以系統時間為種子
	int i;
	for ( i = 0; i < len-1; i++)
	{
		buff[i] = metachar[rand()%num];  //rand（）獲取隨機數序列
	}
}
 

一個合格的偽隨機數生成器需要具備長週期（避免短數列不斷重複）和嚴謹的演算法（驗證其具備不可預測性），下面我具體列舉一些偽隨機數生成器的演算法：

線性同餘法

如C的rand函式和JAVA的java.util.Random類就是使用線性同餘法，其為弱偽隨機數演算法，公式為：

R_n+1 = ( A x R_n + C )modM

例如第一個偽隨機數 R₀ = ( A x 種子 + C)modM

其中A、C、M為常量，A<M,C<M

第二個偽隨機數R₁ = ( A x R₀  + C)modM

該演算法生成的隨機數列範圍在0～M-1之間，演算法的函式實現為

static int A_,C_,M_,R0_;
int Init(int a, int c, int m, int r0)
{
        if( a>m | c>m)
        {
                return -1;
        }
        A_=a;
        C_=c;
        M_=m;
        R0_=r0;
        return 0;
}
void Liner_Congruece(int *buff, int len)
{
        int i;
        for(i=0; i<len; i++)
        {
                buff[i] =(R0_*A_ + C_)%M_;
                R0_=buff[i];
        }
}
 

單向雜湊函式法

單向雜湊函式在之前的篇章中有提過，利用單向雜湊函式可以對一組資料生成特定的雜湊值。

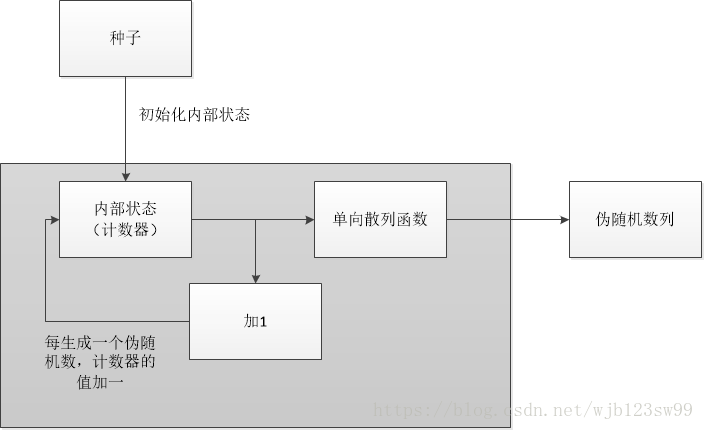
在本章中將利用單向雜湊函式生成具備不可預測性的強偽隨機數生成器。該演算法的生成器將之前有進一步優化其結構為：

從隨機數生成器結構上我們可以清楚的瞭解到，該演算法利用了單向雜湊函式的強碰撞性和單向性使得偽隨機數生成器擁有不可預知性，使得攻擊者即便得到演算法和當前隨機數也無法推算出下一列隨機數值，除非攻擊者能獲得之前所有的隨機數。下面利用SHA-1來實現具體的函式:

#include <stdio.h>
#include <stdlib.h>
#define SHA1_ROTL(a,b) (SHA1_tmp=(a),((SHA1_tmp>>(32-b))&(0x7fffffff>>(31-b)))|(SHA1_tmp<<b))
#define SHA1_F(B,C,D,t) ((t<40)?((t<20)?((B&C)|((~B)&D)):(B^C^D)):((t<60)?((B&C)|(B&D)|(C&D)):(B^C^D)))
long SHA1_tmp;
extern char* StrSHA1(const char* str, long long length, char* sha1){
    /*
    計算字串SHA-1
    引數說明：
    str         字串指標
    length      字串長度
    sha1         用於儲存SHA-1的字串指標
    返回值為引數sha1
    */
    char *pp, *ppend;
    long l, i, K[80], W[80], TEMP, A, B, C, D, E, H0, H1, H2, H3, H4;
    H0 = 0x67452301, H1 = 0xEFCDAB89, H2 = 0x98BADCFE, H3 = 0x10325476, H4 = 0xC3D2E1F0;
    for (i = 0; i < 20; K[i++] = 0x5A827999);
    for (i = 20; i < 40; K[i++] = 0x6ED9EBA1);
    for (i = 40; i < 60; K[i++] = 0x8F1BBCDC);
    for (i = 60; i < 80; K[i++] = 0xCA62C1D6);
    l = length + ((length % 64 > 56) ? (128 - length % 64) : (64 - length % 64));
    if (!(pp = (char*)malloc((unsigned long)l))) return 0;
    for (i = 0; i < length; pp[i + 3 - 2 * (i % 4)] = str[i], i++);
    for (pp[i + 3 - 2 * (i % 4)] = 128,i++; i < l; pp[i + 3 - 2 * (i % 4)] = 0,i++);
    *((long*)(pp + l - 4)) = length << 3;
    *((long*)(pp + l - 8)) = length >> 29;
    for (ppend = pp + l; pp < ppend; pp += 64){
        for (i = 0; i < 16; W[i] = ((long*)pp)[i], i++);
        for (i = 16; i < 80; W[i] = SHA1_ROTL((W[i - 3] ^ W[i - 8] ^ W[i - 14] ^ W[i - 16]), 1), i++);
        A = H0, B = H1, C = H2, D = H3, E = H4;
        for (i = 0; i < 80; i++){
            TEMP = SHA1_ROTL(A, 5) + SHA1_F(B, C, D, i) + E + W[i] + K[i];
            E = D, D = C, C = SHA1_ROTL(B, 30), B = A, A = TEMP;
        }
        H0 += A, H1 += B, H2 += C, H3 += D, H4 += E;
    }
    free(pp - l);
    sprintf(sha1, "%08X%08X%08X%08X%08X", H0, H1, H2, H3, H4); 
    return sha1;
}

static char *seed_;  //種子
static num_=0;  //計數器

void Init(char *seed)
{
	seed_ = seed;
}

void SHA1_Rand(char *buff ,int bufflen)
{
	int i;
	char sha1buff[33] = {0};
	char str[1024]={0};
	
	while(bufflen/32!=0)
	{
		bufflen-=32;
		sprintf(str, "%s%d", seed_, num_++);
		StrSHA1(str, strlen(str), sha1buff);
		sprintf(buff, "%s%s", buff, sha1buff);
	}
	sprintf(str, "%s%d", seed_, num_++);
	StrSHA1(str, strlen(str), sha1buff);
	strncpy(str, sha1buff, bufflen%32);
}

int main()
{
	char *buff = "hello world";  //種子
	Init(buff);
	char key[65] ={0};
	SHA1_Rand(key, 64);
	printf("%s\n", key);
}

密碼法:

與單向雜湊法相似,密碼法利用加密輸出隨機數實現隨機數的不可預知性,其加密可以採用對稱加密AES演算法，或者公鑰演算法其結構為:

密碼法的函式實現可以參照單向雜湊函式，這裡不再列寫。

此外如果對隨機性強度還是不滿足，可以瞭解下ANSI X9.17。一般來說以上三種強偽隨機數演算法已滿足大多數需求。