在之前緬懷金大俠的文章“永遠的金大俠-人工智慧的江湖”中提到：整合學習是機器學習中一種特殊的存在，自有其深厚而樸實的武功哲學，能化腐朽為神奇，變弱學習為強學習，雖不及武當和少林那樣內力與功底深厚。其門下兩個主要分支-Bagging和Boosting，各有成就，前者有隨機森林支撐門面，後者有AdaBoost，GBDT，XGBoost一脈傳承。門下弟子近年來在Kaggle大賽中獲獎無數，體現了實用主義的風格，為眾多習武之人所喜愛，趨之若鶩。

整合學習（ensemble learning）是機器學習裡一個重要、龐大的分支，它體現了一種樸素的哲學思想：

將一些簡單的機器學習模型組合起來使用，可以得到一個強大的模型

即使每個簡單的模型能力很弱，預測精度非常低，但組合起來之後，精度得到了顯著的提升，可以和其他型別的強模型相媲美。在這裡，我們稱簡單的模型為弱學習器（weak learner），組合起來後形成的模型為強學習器（strong learner）。

這種做法在我們的日常生活中隨處可見，比如集體投票決策，這種手段可以讓我們做出更準確的決策。在機器學習領域，這種做法也獲得了成功，理論分析和實驗結果、實踐經驗證明，整合學習是有效的。
決策樹很多情況下，整合學習的若學習器使用決策樹（但也不是絕對的）。因為決策樹實現簡單，計算效率高。在SIGAI之前的公眾號文章“理解決策樹”中已經介紹了決策樹的原理。決策樹是一種基於規則的方法，它用一組巢狀的規則進行預測。在樹的每個決策節點處，根據判斷結果進入一個分支，反覆執行這種操作直到到達葉子節點，得到預測結果。這些規則通過訓練得到，而不是人工制定的。在各種機器學習演算法中，決策樹是非常貼近人的思維的方法，具有很強的可解釋性。

決策樹的預測演算法很簡單，從根節點開始，在樹的每個節點處，用特徵向量中的一個分量與決策樹節點的判定閾值進行比較，然後決定進入左子節點還是右子節點。反覆執行這種操作，直到到達葉子節點處，葉子節點中儲存著類別值（對分類問題）或者回歸值（對迴歸問題），作為預測結果。

訓練時，遞迴的建立樹，從根節點開始。用每個節點的訓練樣本集進行分裂，尋找一個最佳分裂，作為節點的判定規則。同時把訓練樣本集一分為二，用兩個子集分別訓練左子樹和右子樹。

目前已經有多種決策樹的實現，包括ID3[1,2]，C4.5[3]，CART（Classification and Regression Tree，分類與迴歸樹）[4]等，它們的區別主要在於樹的結構與構造演算法。其中分類與迴歸樹既支援分類問題，也可用於迴歸問題，在整合學習中使用的最廣。

分類樹的對映函式是對多維空間的分段線性劃分，即用平行於各座標軸的超平面對空間進行切分；迴歸樹的對映函式是分段常數函式。只要劃分的足夠細，分段常數函式可以逼近閉區間上任意函式到任意指定精度，因此決策樹在理論上可以對任意複雜度的資料進行擬合。關於

決策樹的詳細原理可以閱讀SIGAI之前的公眾號文章《理解決策樹》。
整合學習前面已經說過，整合學習（ensemble learning）通過多個機器學習模型的組合形成一個精度更高的模型，參與組合的模型稱為弱學習器（weak learner）。在預測時使用這些弱學習器模型聯合進行預測，訓練時需要用訓練樣本集依次訓練出這些弱學習器。

根據訓練各個弱學習器的不同思路，目前廣為使用的有兩種方案：

Bagging和Boosting（Stacking在這裡不做介紹）

前者通過對原始訓練樣本集進行隨機抽樣，形成不同的訓練樣本集來訓練每個弱學習器，各個弱學習器之間可以認為近似是獨立的，典型代表是隨機森林；後者為訓練樣本增加權重（AdaBoost），或者構造標籤值（GBDT）來依次訓練每個弱學習器，各個弱學習器之間相關，後面的弱學習器利用了前面的弱學習器的資訊。下面分別對這兩類演算法進行介紹。
Bagging-隨機抽樣訓練每個弱學習器Bagging的核心思想是對訓練樣本集進行抽樣，形成新的訓練樣本集，以此訓練各個弱學習器。由於每個弱學習器使用了不同的樣本集，因此各不相同。預測時，用每個弱學習器分別進行預測，然後投票。在這裡，每個弱學習器的地位是相等的。
隨機森林-獨立學習，平等投票Bagging的典型代表是隨機森林，由Breiman等人提出[5]，它由多棵決策樹組成。預測時，對於分類問題，一個測試樣本會送到每一棵決策樹中進行預測，然後投票，得票最多的類為最終分類結果。對於迴歸問題隨機森林的預測輸出是所有決策樹輸出的均值。

訓練時，使用bootstrap抽樣來構造每個弱學習器的訓練樣本集。這種抽樣的做法是在n個樣本的集合中有放回的抽取n個樣本形成一個數據集。在新的資料集中原始樣本集中的一個樣本可能會出現多次，也可能不出現。隨機森林在訓練時依次訓練每一棵決策樹，每棵樹的訓練樣本都是從原始訓練集中進行隨機抽樣得到。在訓練決策樹的每個節點時所用的特徵也是隨機抽樣得到的，即從特徵向量中隨機抽出部分特徵參與訓練。即隨機森林對訓練樣本和特徵向量的分量都進行了隨機取樣。

正是因為有了這些隨機性，隨機森林可以在一定程度上消除過擬合。對樣本進行取樣是必須的，如果不進行取樣，每次都用完整的訓練樣本集訓練出來的多棵樹是相同的。隨機森林使用多棵決策樹聯合進行預測可以降低模型的方差。隨機深林的介紹請閱讀SIGAI之前的文章《隨機森林概述》
Boosting-序列訓練每個弱學習器Boosting演算法（提升）採用了另外一種思路。預測時用每個弱學習器分別進行預測，然後投票得到結果；訓練時依次訓練每個弱學習器，但不是對樣本進行獨立的隨機抽樣構造訓練集，而是重點關注被前面的弱學習器錯分的樣本。
AdaBoost-吸取前人的教訓，能者多“勞”Boosting作為一種抽象框架很早就被提出[6]，但一直沒有很好的具體實現。AdaBoost演算法（Adaptive Boosting，自適應Boosting）由Freund等人提出[7-11]，是Boosting演算法的一種實現版本。在最早的版本中，這種方法的弱分類器帶有權重，分類器的預測結果為弱分類器預測結果的加權和。訓練時訓練樣本具有權重，並且會在訓練過程中動態調整，被前面的弱分類器錯分的樣本會加大權重，因此演算法會更關注難分的樣本。2001年級聯的AdaBoost分類器被成功用於人臉檢測問題，此後它在很多模式識別問題上得到了應用。

基本的AdaBoost演算法是一種二分類演算法，用弱分類器的線性組合構造強分類器。弱分類器的效能不用太好，僅比隨機猜測強，依靠它們可以構造出一個非常準確的強分類器。強分類器的計算公式為：

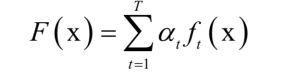
其中x是輸入向量，F(x)是強分類器，  是弱分類器，  是弱分類器的權重，T為弱分類器的數量，弱分類器的輸出值為+1或-1，分別對應正樣本和負樣本。分類時的判定規則為：

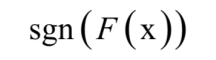
強分類器的輸出值也為+1或-1。弱分類器、重通過訓練演算法得到。

訓練時，依次訓練每一個弱分類器，並得到它們的權重值。訓練樣本也帶有權重值，初始時所有樣本的權重相等，在訓練過程中，被前面的弱分類器錯分的樣本會加大權重，反之會減小權重，這樣接下來的弱分類器會更加關注這些難分的樣本。弱分類器的權重值根據它的準確率構造，精度越高的弱分類器權重越大。

給定l個訓練樣本(  ,  )，其中是特徵向量，為類別標籤，其值為+1或-1。訓練演算法的流程為：
初始化樣本權重值，所有樣本的初始權重相等：

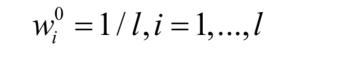
迴圈，對t=1,...,T依次訓練每個弱分類器：
訓練一個弱分類器  ，並計算它對訓練樣本集的錯誤率  
計算弱分類器的權重：

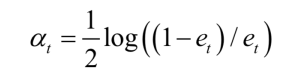
更新所有樣本的權重：

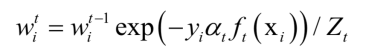
其中  為歸一化因子，它是所有樣本的權重之和：

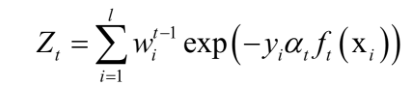
結束迴圈
最後得到強分類器：

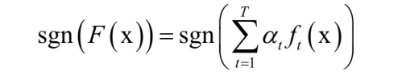
根據計算公式，錯誤率低的弱分類器權重大，它是準確率的增函式。AdaBoost訓練和預測演算法的原理可以閱讀SIGAI之前的公眾號文章“大話AdaBoost演算法”，“理解AdaBoost演算法”。AdaBoost演算法的核心思想是：

關注之前被錯分的樣本，準確率高的弱分類器有更大的權重

文獻[12]用廣義加法模型[6]和指數損失函式解釋了AdaBoost演算法的優化目標，並推匯出其訓練演算法。廣義加法模型用多個基函式的加權組合來表示要擬合的目標函式。

AdaBoost演算法採用了指數損失函式，強分類器對單個訓練樣本的損失函式為：

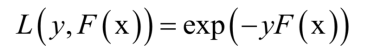
將廣義加法模型的預測函式代入上面的損失函式中，得到演算法訓練時要優化的目標函式為：

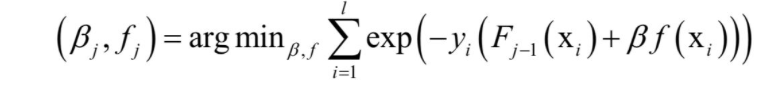
這裡將指數函式拆成了兩部分，已有的強分類器  ，以及當前弱分類器f對訓練樣本的損失函式，前者在之前的迭代中已經求出，因此可以看成常數。這樣目標函式可以簡化為：

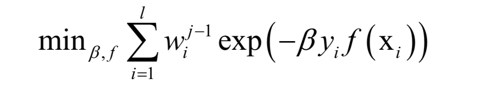
其中：

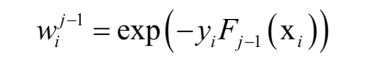
它只和前面的迭代得到的強分類器有關，與當前的弱分類器、弱分類器權重無關，這就是樣本權重。這個問題可以分兩步求解，首先將β看成常數，優化弱分類器。得到弱分類器f()之後，優化目標可以表示成β的函式，然後優化β。

文獻[12]還介紹了四種類型的AdaBoost演算法[7]，它們的弱分類器不同，訓練時優化的目標函式也不同。

離散型AdaBoost演算法就是之前介紹的AdaBoost演算法，從廣義加法模型推匯出了它的訓練演算法。它用牛頓法求解加法logistic迴歸模型。

實數型AdaBoost演算法弱分類器的輸出值是實數值，它是向量到實數的對映。這個實數的絕對值可以看作是置信度，它的值越大，樣本被判定為正樣本的可信度越高。

廣義加性模型沒有限定損失函式的具體型別，離散型和實數型AdaBoost採用的是指數損失函式。如果把logistic迴歸的損失函式應用於此模型，可以得到LogitBoost的損失函式：

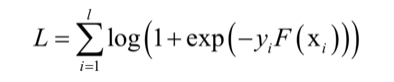
LogitBoost用牛頓法優化logistic迴歸的對數似然函式。

Gentle型AdaBoost的弱分類器是迴歸函式，和實數型AdaBoost類似。

標準的AdaBoost演算法只能用於二分類問題，它的改進型可以用於多類分類問題[8]，典型的實現有AdaBoost.MH演算法，多類Logit型AdaBoost。AdaBoost.MH通過二分類器的組合形成多分類模型，採用了一對多的方案。多類Logit型AdaBoost採用了類似於softmax迴歸的方案。另外，AdaBoost還可以用於迴歸問題，即AdaBoost.R演算法。

與隨機森林不同，AdaBoost演算法的目標主要是降低模型的偏差。文獻[14]從分類間隔的角度對AdaBoost優良的泛化效能進行了解釋。已經證明，AdaBoost演算法在訓練樣本集上的誤差隨著弱分類器的增加呈指數級下降。

AdaBoost演算法在模式識別中最成功的應用之一是機器視覺裡的目標檢測問題，如人臉檢測和行人檢測。在2001年Viola和Jones設計了一種人臉檢測演算法[13]。它使用簡單的Haar特徵和級聯AdaBoost分類器構造檢測器，檢測速度較之前的方法有2個數量級的提高，並且有很高的精度。VJ框架是人臉檢測歷史上有里程碑意義的一個成果，奠定了AdaBoost目標檢測框架的基礎。
GBDT-接力合作，每一杆都更靠近球洞和AdaBoost演算法類似，GBDT（Gradient Boosting Decision Tree，梯度提升樹）[15]也是提升演算法的一種實現，將決策樹用於梯度提升框架，依次訓練每一棵決策樹。GBDT同樣用加法模型表示預測函式，求解時採用了前向擬合。強學習器的預測函式為

其中l為訓練樣本數。這裡取樣了逐步求精的思想，類似於打高爾夫球，先粗略的打一杆，然後在之前的基礎上逐步靠近球洞。具體的思路類似於梯度下降法，將強學習器的輸出值看做一個變數，損失函式L對其求導，將已經求得的強學習器的輸出值  帶入導數計算公式，得到在這一點的導數值，然後取反，得到負梯度方向，當前要求的弱學習器的輸入值如果為這個值，則損失函式的值是下降的。

 

 

由此得到訓練當前弱學習器時樣本的標籤值為。

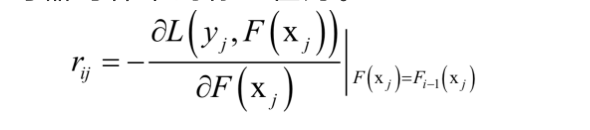
用樣本集(,  )訓練當前的弱學習器，注意，樣本標籤值由已經求得的強學習器決定。

 

如果損失函式使用均方誤差，則負梯度即為殘差，這一般用於迴歸問題。

對於二分類問題，如果用logistic迴歸的對數似然函式做損失函式

 

對於多分類問題，使用交叉熵損失函式，可以得到類似的結果。

得到樣本的標籤值之後，就可以訓練當前的決策樹（弱學習器）。GBDT用損失函式對預測函式的負梯度值作為訓練樣本的標籤值（目標值），訓練當前的決策樹，然後更新強學習器。
XGBoost-顯式正則化，泰勒展開到二階XGBoost[16]是對梯度提升演算法的改進。XGBoost對損失函式進行了改進，由兩部分構成，第一部分為梯度提升演算法的損失函式，第二部分為正則化項

參考文獻
[1] J. Ross Quinlan. Induction of decision trees. Machine Learning, 1986, 1(1): 81-106.
[2] J. Ross Quinlan. Learning efficient classification procedures and their application to chess end games. 1993.
[3] J. Ross Quinlan. C4.5: Programs for Machine Learning. Morgan Kaufmann, San Francisco, CA, 1993.
[4] Breiman, L., Friedman, J. Olshen, R. and Stone C. Classification and Regression Trees, Wadsworth, 1984.
[5] Breiman, Leo. Random Forests. Machine Learning 45 (1), 5-32, 2001.
[6] Robert E Schapire. The Strength of Weak Learnability. Machine Learning, 1990.
[7] Freund, Y. Boosting a weak learning algorithm by majority. Information and Computation, 1995.
[8] Yoav Freund, Robert E Schapire. A decision-theoretic generalization of on-line learning and an application to boosting. computational learning theory. 1995.
[9] Freund, Y. An adaptive version of the boost by majority algorithm. In Proceedings of the Twelfth Annual Conference on Computational Learning Theory, 1999.
[10] R.Schapire. The boosting approach to machine learning: An overview. In MSRI Workshop on Nonlinear Estimation and Classification, Berkeley, CA, 2001.
[11] Freund Y, Schapire RE. A short introduction to boosting. Journal of Japanese Society for Artificial Intelligence, 14(5):771-780. 1999.
[12] Jerome Friedman, Trevor Hastie and Robert Tibshirani. Additive logistic regression: a statistical view of boosting. Annals of Statistics 28(2), 337–407. 2000.
[13] P.Viola and M.Jones. Rapid object detection using a boosted cascade of simple features. In Proceedings IEEE Conf. on Computer Vision and Pattern Recognition, 2001.
[14] Robert E Schapire, Yoav Freund, Peter L Bartlett, Wee Sun Lee. Boosting the margin: a new explanation for the effectiveness of voting methods. Annals of Statistics, 1998.
[15] Jerome H Friedman. Greedy function approximation: A gradient boosting machine. Annals of Statistics, 2001.
[16] Tianqi Chen, Carlos Guestrin. XGBoost: A Scalable Tree Boosting System. knowledge discovery and data mining, 2016.
[17] Guolin Ke, Qi Meng, Thomas Finley, Taifeng Wang, Wei Chen, Weidong Ma, Qiwei Ye, Tieyan Liu. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. neural information processing systems, 2017.