資料結構_棧及其應用
棧及其應用
棧
棧是存放資料物件的一種特殊容器,棧中的元素始終遵循後進先出的順序,作為一種抽象資料型別,棧支援的操作介面如下:
stack<T> S;
S.pop();
S.top();
S.push();
s.empty();
s.size();棧的應用
- 逆序輸出
輸出次序與處理過程顛倒;遞迴深度和輸出長度不易知道。
conversion(進位制轉換)
void convert(stack<char>&s,_int64 n,int base)
{
static char digit[]={'0','1','2','3','4','5' - 遞迴巢狀
具有自相似性的問題可遞迴描述,但分支位置和巢狀深度不固定。
stack permutation+parenthesis(棧混洗和括號匹配)
1、括號匹配
消去一對緊鄰的左右括號,不影響全域性的匹配判斷。
順序掃描表示式,用棧記錄已經掃描的部分,反覆迭代:凡遇到”(“,則進棧;凡遇到”)“,則出棧。
bool paren(const char exp[],int lo,int hi)
{
stack<char>s;
for(int i=0;i<hi;i++)
{
if(exp[i]=='(') //左括號入棧
s.push(exp[i]);
else if(!s.empty())
s.pop();
else 2、棧混洗
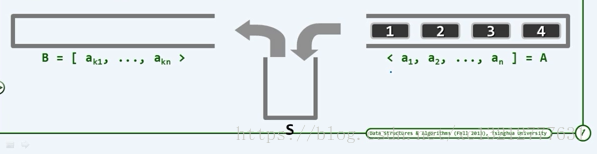
只允許將A的頂元素彈出並壓入s,或將s的頂元素彈出並壓入B中,經過一系列以上操作後,A中的元素全部轉入B中,則稱之為A的一個棧混洗。
對於有n個元素而言他的棧混洗個數記為sp(n);則可以由如下過程推出sp(n)的遞推式:
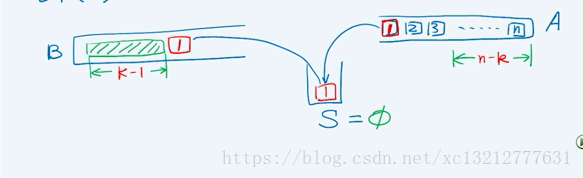
當第一個元素作為第k個元素被推入棧B中時,此時中轉棧應該為空,棧A中還剩下n-k個元素。因為,此時棧B中的K-1個元素的棧混洗個數與剩下的n-k個元素的棧混洗個數相互獨立。則可以推出:

棧混洗的甄別:
我們可以知道任意三個元素能否按照某種相對次序出現於混洗中,與替他元素無關,因此可以推出:

對於上述條件反過來也成立,只要任意序列中不含上述形式,就是一種棧混洗。
演算法:直接藉助棧A,B和S,模擬棧混洗過程,每次在S.pop()之前,檢測S是否為空;或需要彈出的元素在S中,卻不是頂元素。
example:
1、棧的壓入、彈出序列
題目描述:輸入兩個整數序列,第一個序列表示棧的壓入順序,請判斷第二個序列是否為該棧的彈出順序。
分析:實際上這就是一個棧混洗的過程,我們使用上述描述的演算法就可以解決。即:如果下一個彈出的數字剛好是輔助棧S的棧頂數字,那麼直接彈出。如果下一個彈出的數字不在棧頂,我們把壓棧序列中還沒有入棧的數字壓入S中,直到把下一個需要彈出的元素壓入棧頂為止。如果所有元素都壓入了棧還沒有找到下一個彈出的數字,那麼該序列就不是一個棧混洗。
class Solution {
public:
bool IsPopOrder(vector<int> pushv,vector<int> popv) {
stack<int> s; //輔助棧S
int id=0;
for(int i=0;i<popv.size();++i)
{
while(s.empty()||s.top()!=popv[i])
{
s.push(pushv[id++]);
if(id>pushv.size())
return false;
}
s.pop();
}
return true;
}
};棧混洗與括號匹配之間的聯絡,n個元素的棧混洗有多少種,n對括號所能表達的合法表示式就有多少種。
將左括號換成push操作,右括號換成pop操作,
由n對括號構成的一個合法的表示式可以解釋為對n個元素進行棧混洗的合法的過程。
2、包含min函式的棧(擴充套件應用)
題目描述:定義棧的資料結構,在該型別中實現一個能夠得到棧的最小的元素的min函式。
首先最直觀的是我們可以想到在棧裡新增一個成員變數存放最小的元素。每次壓入一個新元素的時候,如果比當前元素還要小,就更新最小元素,但是這時候會存在一個問題,如果當最小元素被彈出棧後,沒法獲得下一個最小元素,以此推廣,我們藉助一個輔助棧S,它用來記錄棧A中每一個元素作為棧頂元素時,棧的最小元素。也就是說,我們把每一次的最小元素都存起來。
class Solution {
public:
void push(int value) {
m_data.push(value);
if(m_min.size()==0||value<m_min.top())
m_min.push(value);
else
m_min.push(m_min.top());
}
void pop() {
m_data.pop();
m_min.pop();
}
int top() {
return m_data.top();
}
int min() {
return m_min.top();
}
private:
stack<int> m_data;
stack<int> m_min;//構造輔助棧 相當於記錄的m_data中的每一位元素作為棧頂元素時,棧中的最小值是多少,若用一個變數記錄最小值,當其彈出時,無法在得到最小值。
};- 延遲緩衝
線上性掃描演算法模式中,在預讀足夠長之後,方能確定可處理的字首。
evaluation(表示式求值)
該演算法自左向右掃描表示式,並對其中字元逐一做相應的處理。那些已經掃描過但是因資訊不足尚不能夠處理的運算元與運算子,將分別緩衝至棧opnd和棧optr中。一旦判定以快取的子表示式優先順序足夠高,便彈出相關的運算元和運算子,隨機執行運算,並將結果壓入棧opnd中。
#define N_OPTR 9 //運算子總數
typedef enum { ADD, SUB, MUL, DIV, POW, FAC, L_P, R_P, EOE } Operator; //運算子集合
//加、減、乘、除、乘方、階乘、左括號、右括號、起始符與終止符
const char pri[N_OPTR][N_OPTR] = { //運算子優先等級 [棧頂] [當前]
/* |-------------------- 當 前 運 算 符 --------------------| */
/* + - * / ^ ! ( ) \0 */
/* -- + */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* | - */ '>', '>', '<', '<', '<', '<', '<', '>', '>',
/* 棧 * */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 頂 / */ '>', '>', '>', '>', '<', '<', '<', '>', '>',
/* 運 ^ */ '>', '>', '>', '>', '>', '<', '<', '>', '>',
/* 算 ! */ '>', '>', '>', '>', '>', '>', ' ', '>', '>',
/* 符 ( */ '<', '<', '<', '<', '<', '<', '<', '=', ' ',
/* | ) */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* -- \0 */ '<', '<', '<', '<', '<', '<', '<', ' ', '='
};
float evaluate ( char* S, char*& RPN ) { //對(已剔除白空格的)表示式S求值,並轉換為逆波蘭式RPN
Stack<float> opnd; Stack<char> optr; //運算數棧、運算子棧
optr.push ( '\0' ); //尾哨兵'\0'也作為頭哨兵首先入棧
while ( !optr.empty() ) { //在運算子棧非空之前,逐個處理表達式中各字元
if ( isdigit ( *S ) ) { //若當前字元為運算元,則
readNumber ( S, opnd ); append ( RPN, opnd.top() ); //讀入運算元,並將其接至RPN末尾
} else //若當前字元為運算子,則
switch ( orderBetween ( optr.top(), *S ) ) { //視其與棧頂運算子之間優先順序高低分別處理
case '<': //棧頂運算子優先順序更低時
optr.push ( *S ); S++; //計算推遲,當前運算子進棧
break;
case '=': //優先順序相等(當前運算子為右括號或者尾部哨兵'\0')時
optr.pop(); S++; //脫括號並接收下一個字元
break;
case '>': { //棧頂運算子優先順序更高時,可實施相應的計算,並將結果重新入棧
char op = optr.pop(); append ( RPN, op ); //棧頂運算子出棧並續接至RPN末尾
if ( '!' == op ) { //若屬於一元運算子
float pOpnd = opnd.pop(); //只需取出一個運算元,並
opnd.push ( calcu ( op, pOpnd ) ); //實施一元計算,結果入棧
} else { //對於其它(二元)運算子
float pOpnd2 = opnd.pop(), pOpnd1 = opnd.pop(); //取出後、前運算元
opnd.push ( calcu ( pOpnd1, op, pOpnd2 ) ); //實施二元計算,結果入棧
}
break;
}
default : exit ( -1 ); //逢語法錯誤,不做處理直接退出
}//switch
}//while
return opnd.pop(); //彈出並返回最後的計算結果
}
- 棧式計算
基於棧結構的特定計算模式。
RPN(逆波蘭表示式)
RPN表示式(字尾表示式):在由運算子和運算元組成的表示式中,不適用括號,即可以表示帶優先順序的運算關係,RPN表示式中運算子的執行次序,可以更為簡潔的確定,既不必在事先做任何約定,也不用括號強制改變優先順序。
由中綴表示式轉換為字尾表示式:
1、手工轉換
對於運算數的順序而言,不會改變,運算元在中綴表示式和字尾表示式中一致。
2、轉換演算法
凡是遇到運算元,即追加至RPN;而運算子只有在從棧中彈出並且執行時,才會被追加。
example:
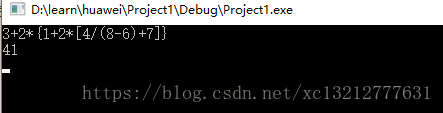
請實現如下介面
/* 功能:四則運算
* 輸入:strExpression:字串格式的算術表示式,如: "3+2*{1+2*[-4/(8-6)+7]}"
* 返回:算術表示式的計算結果
*/
public static int calculate(String strExpression)
{
/* 請實現*/
return 0;
}
約束:
pucExpression字串中的有效字元包括[‘0’-‘9’],‘+’,‘-’, ‘*’,‘/’ ,‘(’, ‘)’,‘[’, ‘]’,‘{’ ,‘}’。
pucExpression算術表示式的有效性由呼叫者保證;
#include<iostream>
#include<string>
#include<stack>
using namespace std;
#define N_OPTR 11 //運算子總數
typedef enum { ADD, SUB, MUL, DIV, L_P, R_P,ML_P,MR_P,BL_P,BR_P,EOE } Operator; //運算子集合
//加、減、乘、除、乘方、階乘、左括號、右括號、起始符與終止符
const char pri[N_OPTR][N_OPTR] = { //運算子優先等級 [棧頂] [當前]
/* |-------------------- 當 前 運 算 符 --------------------| */
/* + - * / ( ) [ ] { } \0 */
/* -- + */ '>', '>', '<', '<', '<', '>', '<', '>', '<', '>', '>',
/* | - */ '>', '>', '<', '<', '<', '>', '<', '>', '<', '>', '>',
/* 棧 * */ '>', '>', '>', '>', '<', '>', '<', '>', '<', '>', '>',
/* 頂 / */ '>', '>', '>', '>', '<', '>', '<', '>', '<', '>', '>',
/* 符 ( */ '<', '<', '<', '<', '<', '=', '<', ' ', '<', ' ', ' ',
/* | ) */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* [ */ '<', '<', '<', '<', '<', '=', '<', '=', '<', ' ', ' ',
/* ] */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* { */ '<', '<', '<', '<', '<', ' ', '<', ' ', '<', '=', ' ',
/* } */ ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ', ' ',
/* \0*/ '<', '<', '<', '<', '<', ' ', '<', ' ', '<', ' ', '='
};
Operator optr2rank(char op)
{
switch (op)
{
case '+': return ADD;
case '-': return SUB;
case '*': return MUL;
case '/': return DIV;
case '(': return L_P;
case ')': return R_P;
case '[': return ML_P;
case ']': return MR_P;
case '{': return BL_P;
case '}': return BR_P;
case '\0':return EOE;
default:
exit(-1);
}
}
char orderbetween(char op1, char op2) //比較兩個運算子之間的優先順序
{
return pri[optr2rank(op1)][optr2rank(op2)];
}
int calc(int popnd1, char op, int popnd2)
{
switch (op)
{
case '+':return popnd1 + popnd2;
case '-':return popnd1 - popnd2;
case '*':return popnd1 * popnd2;
case '/':return popnd1 / popnd2;
default:
exit(-1);
}
}
int evaluate(string &s, string &RPN)
{
stack<int> opnd; stack<char> optr;//運算數棧,操作符棧
optr.push('\0');
s.push_back('\0');
int i = 0;
while(!optr.empty())
{
if (isdigit(s[i])) //如果為運算元
{
int number = 0;
while (isdigit(s[i]))
{
number = number * 10 + s[i] - '0';
i++;
}
opnd.push(number);
RPN += number; //接入RPN末尾
}
else //如果為操作符
{
if (s[i] == '-' && (s[i - 1] == '(' || s[i - 1] == '[' || s[i - 1] == '{'))//對於負數處理就在前面加0即可。
opnd.push(0);
switch (orderbetween(optr.top(),s[i]))//比較當前運算子與棧頂運算子之間的優先順序
{
case '<': //棧頂元素優先順序更低時
optr.push(s[i]);
++i;
break;
case'=': //優先順序相等,當前運算子為右括號
optr.pop(); //脫掉括號 接收下一個字元
++i;
break;
case'>':
{
//棧頂運算子優先順序更高時,可以實施相應的計算並且將結果重新入棧。
char op =optr.top();
RPN += op; //棧頂元素出棧加入RPN末尾
optr.pop();
int popnd2 = opnd.top(); opnd.pop();
int popnd1 = opnd.top(); opnd.pop(); //取出後前兩個運算元
opnd.push(calc(popnd1, op, popnd2)); //將計算的結果壓入棧中
break;
}
default:
exit(-1);// 錯誤時不做處理直接退出。
}
}
}
return opnd.top();
}
int main()
{
string str;
while (cin>>str)
{
string RPN;
cout << evaluate(str, RPN) << endl;
}
}