Wasserstein GAN最新進展：從weight clipping到gradient penalty，更加先進的Lipschitz限制手法

阿新 • • 發佈：2018-12-27

前段時間，Wasserstein GAN以其精巧的理論分析、簡單至極的演算法實現、出色的實驗效果，在GAN研究圈內掀起了一陣熱潮（對WGAN不熟悉的讀者，可以參考我之前寫的介紹文章：令人拍案叫絕的Wasserstein GAN - 知乎專欄）。但是很多人（包括我們實驗室的同學）到了上手跑實驗的時候，卻發現WGAN實際上沒那麼完美，反而存在著訓練困難、收斂速度慢等問題。其實，WGAN的作者Martin Arjovsky不久後就在reddit上表示他也意識到了這個問題，認為關鍵在於原設計中Lipschitz限制的施加方式不對，並在新論文中提出了相應的改進方案：

首先回顧一下WGAN的關鍵部分——Lipschitz限制是什麼。

WGAN中，判別器D和生成器G的loss函式分別是：

$L(D) = -\mathbb{E}_{x\sim P_r}[D(x)] + \mathbb{E}_{x\sim P_g}[D(x)]$ （公式1）

$L(G) = - \mathbb{E}_{x\sim P_g}[D(x)]$ （公式2）

公式1表示判別器希望儘可能拉高真樣本的分數，拉低假樣本的分數，公式2表示生成器希望儘可能拉高假樣本的分數。

Lipschitz限制則體現為，在整個樣本空間 $\mathcal{X}$ 上，要求判別器函式D(x)梯度的Lp-norm不大於一個有限的常數K：

$|| \nabla _x D(x) ||_p \leq K \text{, } \forall x \in \mathcal{X}$ （公式3）

直觀上解釋，就是當輸入的樣本稍微變化後，判別器給出的分數不能發生太過劇烈的變化。在原來的論文中，這個限制具體是通過weight clipping的方式實現的：每當更新完一次判別器的引數之後，就檢查判別器的所有引數的絕對值有沒有超過一個閾值，比如0.01，有的話就把這些引數clip回 [-0.01, 0.01] 範圍內。通過在訓練過程中保證判別器的所有引數有界，就保證了判別器不能對兩個略微不同的樣本給出天差地別的分數值，從而間接實現了Lipschitz限制。

然而weight clipping的實現方式存在兩個嚴重問題：

第一，如公式1所言，判別器loss希望儘可能拉大真假樣本的分數差，然而weight clipping獨立地限制每一個網路引數的取值範圍，在這種情況下我們可以想象，最優的策略就是儘可能讓所有引數走極端，要麼取最大值（如0.01）要麼取最小值（如-0.01）！為了驗證這一點，作者統計了經過充分訓練的判別器中所有網路引數的數值分佈，發現真的集中在最大和最小兩個極端上：

&lt;img src="https://pic2.zhimg.com/v2-7a3aedf9fa60ce660bff9f03935d8f15_b.jpg" data-rawwidth="636" data-rawheight="541" class="origin_image zh-lightbox-thumb" width="636" data-original="https://pic2.zhimg.com/v2-7a3aedf9fa60ce660bff9f03935d8f15_r.jpg"&gt;

這樣帶來的結果就是，判別器會非常傾向於學習一個簡單的對映函式（想想看，幾乎所有引數都是正負0.01，都已經可以直接視為一個二值神經網路了，太簡單了）。而作為一個深層神經網路來說，這實在是對自身強大擬合能力的巨大浪費！判別器沒能充分利用自身的模型能力，經過它回傳給生成器的梯度也會跟著變差。

在正式介紹gradient penalty之前，我們可以先看看在它的指導下，同樣充分訓練判別器之後，引數的數值分佈就合理得多了，判別器也能夠充分利用自身模型的擬合能力：

&lt;img src="https://pic3.zhimg.com/v2-27afb895eea82f5392b19ca770865b96_b.jpg" data-rawwidth="1303" data-rawheight="543" class="origin_image zh-lightbox-thumb" width="1303" data-original="https://pic3.zhimg.com/v2-27afb895eea82f5392b19ca770865b96_r.jpg"&gt;

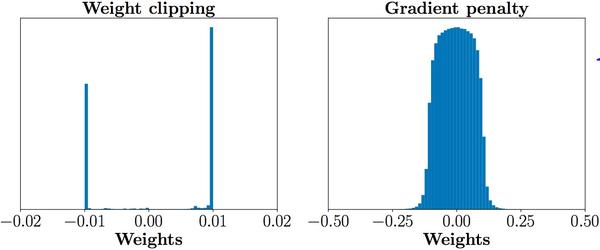
第二個問題，weight clipping會導致很容易一不小心就梯度消失或者梯度爆炸。原因是判別器是一個多層網路，如果我們把clipping threshold設得稍微小了一點，每經過一層網路，梯度就變小一點點，多層之後就會指數衰減；反之，如果設得稍微大了一點，每經過一層網路，梯度變大一點點，多層之後就會指數爆炸。只有設得不大不小，才能讓生成器獲得恰到好處的回傳梯度，然而在實際應用中這個平衡區域可能很狹窄，就會給調參工作帶來麻煩。相比之下，gradient penalty就可以讓梯度在後向傳播的過程中保持平穩。論文通過下圖體現了這一點，其中橫軸代表判別器從低到高第幾層，縱軸代表梯度回傳到這一層之後的尺度大小（注意縱軸是對數刻度），c是clipping threshold：

&lt;img src="https://pic2.zhimg.com/v2-34114a10c56518d606c1b5dd77f64585_b.jpg" data-rawwidth="723" data-rawheight="546" class="origin_image zh-lightbox-thumb" width="723" data-original="https://pic2.zhimg.com/v2-34114a10c56518d606c1b5dd77f64585_r.jpg"&gt;

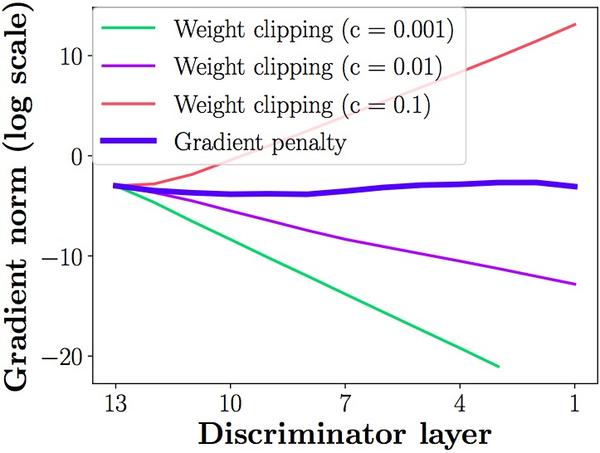
說了這麼多，gradient penalty到底是什麼？

前面提到，Lipschitz限制是要求判別器的梯度不超過K，那我們何不直接設定一個額外的loss項來體現這一點呢？比如說：

$ReLU[ || \nabla_x D(x) ||_p - K ]$ （公式4）

不過，既然判別器希望儘可能拉大真假樣本的分數差距，那自然是希望梯度越大越好，變化幅度越大越好，所以判別器在充分訓練之後，其梯度norm其實就會是在K附近。知道了這一點，我們可以把上面的loss改成要求梯度norm離K越近越好，效果是類似的：

$[ || \nabla_x D(x) ||_p - K ]^2$ （公式5）

究竟是公式4好還是公式5好，我看不出來，可能需要實驗驗證，反正論文作者選的是公式5。接著我們簡單地把K定為1，再跟WGAN原來的判別器loss加權合併，就得到新的判別器loss：

$L(D) = -\mathbb{E}_{x\sim P_r}[D(x)] + \mathbb{E}_{x\sim P_g}[D(x)] + \lambda \mathbb{E}_{x \sim \mathcal{X}} [ || \nabla_x D(x) ||_p - 1 ]^2$ （公式6）

這就是所謂的gradient penalty了嗎？還沒完。公式6有兩個問題，首先是loss函式中存在梯度項，那麼優化這個loss豈不是要算梯度的梯度？一些讀者可能對此存在疑惑，不過這屬於實現上的問題，放到後面說。

其次，3個loss項都是期望的形式，落到實現上肯定得變成取樣的形式。前面兩個期望的取樣我們都熟悉，第一個期望是從真樣本集裡面採，第二個期望是從生成器的噪聲輸入分佈取樣後，再由生成器對映到樣本空間。可是第三個分佈要求我們在整個樣本空間 $\mathcal{X}$ 上取樣，這完全不科學！由於所謂的維度災難問題，如果要通過取樣的方式在圖片或自然語言這樣的高維樣本空間中估計期望值，所需樣本量是指數級的，實際上沒法做到。

所以，論文作者就非常機智地提出，我們其實沒必要在整個樣本空間上施加Lipschitz限制，只要重點抓住生成樣本集中區域、真實樣本集中區域以及夾在它們中間的區域就行了。具體來說，我們先隨機採一對真假樣本，還有一個0-1的隨機數：

$x_r \sim P_r, x_g \sim P_g, \epsilon \sim Uniform[0, 1]$ （公式7）

然後在 $x_r$ 和 $x_g$ 的連線上隨機插值取樣：

$\hat x = \epsilon x_r + (1 - \epsilon) x_g$ （公式8）

把按照上述流程取樣得到的 $\hat x$ 所滿足的分佈記為 $P_{\hat x}$ ，就得到最終版本的判別器loss：

$L(D) = -\mathbb{E}_{x\sim P_r}[D(x)] + \mathbb{E}_{x\sim P_g}[D(x)] + \lambda \mathbb{E}_{x \sim \mathcal{P_{\hat x}}} [ || \nabla_x D(x) ||_p - 1 ]^2$ （公式9）

這就是新論文所採用的gradient penalty方法，相應的新WGAN模型簡稱為WGAN-GP。我們可以做一個對比：

weight clipping是對樣本空間全域性生效，但因為是間接限制判別器的梯度norm，會導致一不小心就梯度消失或者梯度爆炸；
gradient penalty只對真假樣本集中區域、及其中間的過渡地帶生效，但因為是直接把判別器的梯度norm限制在1附近，所以梯度可控性非常強，容易調整到合適的尺度大小。

論文還講了一些使用gradient penalty時需要注意的配套事項，這裡只提一點：由於我們是對每個樣本獨立地施加梯度懲罰，所以判別器的模型架構中不能使用Batch Normalization，因為它會引入同個batch中不同樣本的相互依賴關係。如果需要的話，可以選擇其他normalization方法，如Layer Normalization、Weight Normalization和Instance Normalization，這些方法就不會引入樣本之間的依賴。論文推薦的是Layer Normalization。

實驗表明，gradient penalty能夠顯著提高訓練速度，解決了原始WGAN收斂緩慢的問題：

&lt;img src="https://pic4.zhimg.com/v2-5b01ef93f60a14e7fa10dbea2b620627_b.jpg" data-rawwidth="1255" data-rawheight="479" class="origin_image zh-lightbox-thumb" width="1255" data-original="https://pic4.zhimg.com/v2-5b01ef93f60a14e7fa10dbea2b620627_r.jpg"&gt;

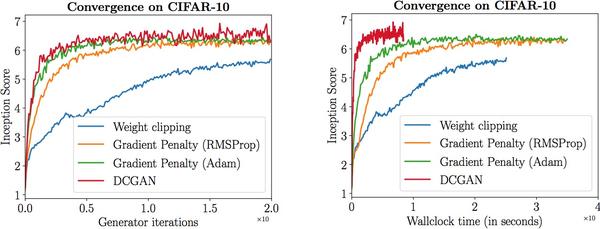
雖然還是比不過DCGAN，但是因為WGAN不存在平衡判別器與生成器的問題，所以會比DCGAN更穩定，還是很有優勢的。不過，作者憑什麼能這麼說？因為下面的實驗體現出，在各種不同的網路架構下，其他GAN變種能不能訓練好，可以說是一件相當看人品的事情，但是WGAN-GP全都能夠訓練好，尤其是最下面一行所對應的101層殘差神經網路：

&lt;img src="https://pic2.zhimg.com/v2-e0a3d86ccfa101a4d3fee1c0cef96a81_b.jpg" data-rawwidth="835" data-rawheight="1279" class="origin_image zh-lightbox-thumb" width="835" data-original="https://pic2.zhimg.com/v2-e0a3d86ccfa101a4d3fee1c0cef96a81_r.jpg"&gt;

剩下的實驗結果中，比較厲害的是第一次成功做到了“純粹的”的文字GAN訓練！我們知道在影象上訓練GAN是不需要額外的有監督資訊的，但是之前就沒有人能夠像訓練影象GAN一樣訓練好一個文字GAN，要麼依賴於預訓練一個語言模型，要麼就是利用已有的有監督ground truth提供指導資訊。而現在WGAN-GP終於在無需任何有監督資訊的情況下，生成出下圖所示的英文字元序列：

&lt;img src="https://pic1.zhimg.com/v2-33c3af150f9bd52485b800948d3cb700_b.jpg" data-rawwidth="1056" data-rawheight="769" class="origin_image zh-lightbox-thumb" width="1056" data-original="https://pic1.zhimg.com/v2-33c3af150f9bd52485b800948d3cb700_r.jpg"&gt;

它是怎麼做到的呢？我認為關鍵之處是對樣本形式的更改。以前我們一般會把文字這樣的離散序列樣本表示為sequence of index，但是它把文字表示成sequence of probability vector。對於生成樣本來說，我們可以取網路softmax層輸出的詞典概率分佈向量，作為序列中每一個位置的內容；而對於真實樣本來說，每個probability vector實際上就蛻化為我們熟悉的onehot vector。

但是如果按照傳統GAN的思路來分析，這不是作死嗎？一邊是hard onehot vector，另一邊是soft probability vector，判別器一下子就能夠區分它們，生成器還怎麼學習？沒關係，對於WGAN來說，真假樣本好不好區分並不是問題，WGAN只是拉近兩個分佈之間的Wasserstein距離，就算是一邊是hard onehot另一邊是soft probability也可以拉近，在訓練過程中，概率向量中的有些項可能會慢慢變成0.8、0.9到接近1，整個向量也會接近onehot，最後我們要真正輸出sequence of index形式的樣本時，只需要對這些概率向量取argmax得到最大概率的index就行了。

新的樣本表示形式+WGAN的分佈拉近能力是一個“黃金組合”，但除此之外，還有其他因素幫助論文作者跑出上圖的效果，包括：

文字粒度為英文字元，而非英文單詞，所以字典大小才二三十，大大減小了搜尋空間
文字長度也才32
生成器用的不是常見的LSTM架構，而是多層反捲積網路，輸入一個高斯噪聲向量，直接一次性轉換出所有32個字元

上面第三點非常有趣，因為它讓我聯想到前段時間挺火的語言學科幻電影《降臨》：

&lt;img src="https://pic4.zhimg.com/v2-be3b9c574b9c1b1ac05d0d462a04acd7_b.jpg" data-rawwidth="1280" data-rawheight="1998" class="origin_image zh-lightbox-thumb" width="1280" data-original="https://pic4.zhimg.com/v2-be3b9c574b9c1b1ac05d0d462a04acd7_r.jpg"&gt;

裡面的外星人“七肢怪”所使用的語言跟人類不同，人類使用的是線性的、序列的語言，而“七肢怪”使用的是非線性的、並行的語言。“七肢怪”在跟主角交流的時候，都是一次性同時給出所有的語義單元的，所以說它們其實是一些多層反捲積網路進化出來的人工智慧生命嗎？

&lt;img src="https://pic3.zhimg.com/v2-f45cc71a24451e1c8d650dba9001a406_b.png" data-rawwidth="2000" data-rawheight="838" class="origin_image zh-lightbox-thumb" width="2000" data-original="https://pic3.zhimg.com/v2-f45cc71a24451e1c8d650dba9001a406_r.png"&gt;

&lt;img src="https://pic1.zhimg.com/v2-1ff948ae23ed8c19bfb4bedf6f466744_b.jpg" data-rawwidth="1622" data-rawheight="690" class="origin_image zh-lightbox-thumb" width="1622" data-original="https://pic1.zhimg.com/v2-1ff948ae23ed8c19bfb4bedf6f466744_r.jpg"&gt;

開完腦洞，我們回過頭看，不得不承認這個實驗的setup實在過於簡化了，能否擴充套件到更加實際的複雜場景，也會是一個問題。但是不管怎樣，生成出來的結果仍然是突破性的。

最後說回gradient penalty的實現問題。loss中本身包含梯度，優化loss就需要求梯度的梯度，這個功能並不是現在所有深度學習框架的標配功能，不過好在Tensorflow就有提供這個介面——tf.gradients。開頭連結的GitHub原始碼中就是這麼寫的：

# interpolates就是隨機插值取樣得到的影象，gradients就是loss中的梯度懲罰項
gradients = tf.gradients(Discriminator(interpolates), [interpolates])[0]

對於我這樣的PyTorch黨就非常不幸了，高階梯度的功能還在開發，感興趣的PyTorch黨可以訂閱這個GitHub的pull request：Autograd refactor，如果它被merged了話就可以在最新版中使用高階梯度的功能實現gradient penalty了。但是除了等待我們就沒有別的辦法了嗎？其實可能是有的，我想到了一種近似方法來實現gradient penalty，只需要把微分換成差分：

$L(D) = -\mathbb{E}_{x\sim P_r}[D(x)] + \mathbb{E}_{x\sim P_g}[D(x)] + \lambda \mathbb{E}_{x_1 \sim \mathcal{P_{\hat x}}, \ x_2 \sim \mathcal{P_{\hat x}}} [ \frac{|D(x_1) -D(x_2)|}{ || x_1 - x_2 ||_p } - 1]^2$ （公式10）

也就是說，我們仍然是在分佈 $P_{\hat x}$ 上隨機取樣，但是一次採兩個，然後要求它們的連線斜率要接近1，這樣理論上也可以起到跟公式9一樣的效果，我自己在MNIST+MLP上簡單驗證過有作用，PyTorch黨甚至Tensorflow黨都可以嘗試用一下

原文地址：　https://www.zhihu.com/question/52602529/answer/158727900

Wasserstein GAN最新進展：從weight clipping到gradient penalty，更加先進的Lipschitz限制手法

Wasserstein GAN最新進展：從weight clipping到gradient penalty，更加先進的Lipschitz限制手法

GAN學習指南：從原理入門到製作生成Demo

2017年深度學習優化演算法最新進展：改進SGD和Adam方法

塗子沛：從幼稚到成熟，我們這個時代的數據革命

網際網路發展階段的三階段：從門戶到搜尋，到移動網際網路

專訪Josh Wills：從數學到程式設計，如何成為更好的程式設計師？

胡八一：從“交付”到“交易”，阿米巴內部交易結算有標準

python：從迭代器，到生成器，再到協程的示例程式碼

雙11大隊長霜波：從手忙腳亂到胸有成竹，我們如何走過這十年？

####好好好好好#####如何基於Spark做深度學習：從Mllib到keras，elephas

Kafka實戰：從RDBMS到Hadoop，七步實現實時傳輸

最新解決：Discuz! X3.2對不起，您安裝的不是正版應用，安裝程式

如何基於Spark做深度學習：從Mllib到keras，elephas

曾國藩：從30歲起，脫胎換骨

Python程式設計：從入門到實踐，課後題14-2

初學java：從鍵盤輸入字串，並統計其中數字字元的個數

胡喜：從 BASIC 到 basic ，螞蟻金服技術要解決兩個基本的計算問題

一個遊戲是如何被開發出來的：從立項到Beta，遊戲開發全流程解析

更快更穩定：這就是Wasserstein GAN

Dapp快訊｜EOS即時運算量超過ETH；以太坊聯合創始人：專注開發，ETH價格任其漲跌；火幣釋出Hadax專案最新進展

Wasserstein GAN最新進展：從weight clipping到gradient penalty，更加先進的Lipschitz限制手法

相關推薦