深度學習二：使用TensorFlow搭建簡單的全連線神經網路

學習《TensorFlow實戰Google深度學習框架》一書

在前一篇部落格中，學習了使用python搭建簡單的全連線神經網路

深度學習一：搭建簡單的全連線神經網路

這裡繼續學習使用TensorFlow來搭建全連線神經網路。文章結束後依舊會貼上全部程式碼

實驗環境：Python+TensorFlow+Pycharm

實驗依舊採用隨機生成的資料集，用隨機生成的x來擬合隨機生成的y

首先是引入並生成隨機資料：

import tensorflow as tf
from numpy.random import RandomState
import matplotlib.pyplot as plt

# 隨機生成資料集，並自定義標籤
rdm = RandomState(1)
dataset_size = 128  # 資料集大小
X = rdm.rand(dataset_size, 2)
Y = [[int(x1+x2 < 1)] for (x1, x2) in X]  # 生成標籤
 

生成的輸入X維度為（128,2），標籤Y的維度為（128,1），可以認為輸入為產品兩個屬性值x1和x2，如果x1+x2<1則被認為是合格產品，標籤為Y為1，否則標籤Y為0。

定義輸入輸出：

# 定義輸入和標籤（真實值）
x = tf.placeholder("float32", [None, 2])
y_ = tf.placeholder("float32", [None, 1])

這裡的x和y_用來接收輸入的X和Y

設定神經網路的引數：

# 權重
W1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
W2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
# 偏置
b1 = tf.Variable(tf.zeros([3]))
b2 = tf.Variable(tf.zeros([1]))
 

這裡定義的是但隱層神經網路，w1和b1是隱藏層的權重和偏置，w2和b2是輸出層的權重和偏置。設計隱藏層有3個隱藏節點，所以，w1的維度為（2,3）。Tenorflow提供了多種隨機數生成的函式，這裡使用tf.r的andom_normal()生成服從正態分佈的隨機數，tf.zeros則生成全0陣列。

神經網路的前向傳播輸出：

# 輸出
a1 = tf.nn.relu(tf.matmul(x, W1)+b1)
y = tf.nn.relu(tf.matmul(a1, W2)+b2)

tf.nn.relu()函式提供了ReLu啟用函式的實現，tf.matmul則實現了矩陣的乘法。可以看到，a1為隱藏層的輸出，y為輸出層的輸出。

定義網路的訓練：

# 定義損失函式
# cross_entropy = -tf.reduce_sum(y_*tf.log(y)+(1-y_)*tf.log(1-y))
cross_entropy = -tf.reduce_mean(y_*tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
# cross_entropy = - tf.reduce_mean(y_*tf.log(y))
# cross_entropy = - (tf.reduce_mean(y_*tf.log(y))+tf.contrib.layers.l2_regularizer(0.01)(W1))  #加入L2正則
# 學習率

learning_rate = 0.001
# 定義優化方法
# optimizer = tf.train.GradientDescentOptimizer(learning_rate)
optimizer = tf.train.AdamOptimizer(learning_rate)
train_step = optimizer.minimize(cross_entropy)

TensorFlow提供了多種訓練優化方法的實現，很方便。

開始訓練網路：

init = tf.global_variables_initializer()
with tf.Session() as sess:
    # 初始化引數
    sess.run(init)
    # 定義批量大小和迭代次數
    batch_size = 9
    step = 1000
    # 開始訓練
    for i in range(step):
        # 獲取批量訓練的資料
        start = (i*batch_size) % dataset_size
        end = min(start+batch_size, dataset_size)
        # 輸入資料訓練
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 10 == 0:
            # 每10輪迭代獲取一次損失函式的值
            loss = sess.run(cross_entropy, feed_dict={x: X, y_: Y})
            # 輸出繪圖
            print(i, "epoch,loss:", loss)
            plt.plot(i, loss, 'ro')
    plt.show()

相比之下，使用TensorFlow實現的神經網路更加便捷，很多步驟都不需要自己去逐步實現。

全部程式碼如下：

import tensorflow as tf
from numpy.random import RandomState
import matplotlib.pyplot as plt

# 隨機生成資料集，並自定義標籤
rdm = RandomState(1)
dataset_size = 128  # 資料集大小
X = rdm.rand(dataset_size, 2)
Y = [[int(x1+x2 < 1)] for (x1, x2) in X]  # 生成標籤

# 定義輸入和標籤（真實值）
x = tf.placeholder("float32", [None, 2])
y_ = tf.placeholder("float32", [None, 1])
# 權重
W1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
W2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))
# 偏置
b1 = tf.Variable(tf.zeros([3]))
b2 = tf.Variable(tf.zeros([1]))

# 輸出
a1 = tf.nn.relu(tf.matmul(x, W1)+b1)
y = tf.nn.relu(tf.matmul(a1, W2)+b2)

# 定義損失函式
# cross_entropy = -tf.reduce_sum(y_*tf.log(y)+(1-y_)*tf.log(1-y))
cross_entropy = -tf.reduce_mean(y_*tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
# cross_entropy = - tf.reduce_mean(y_*tf.log(y))
# cross_entropy = - (tf.reduce_mean(y_*tf.log(y))+tf.contrib.layers.l2_regularizer(0.01)(W1))  #加入L2正則
# 學習率

learning_rate = 0.001
# 定義優化方法
# optimizer = tf.train.GradientDescentOptimizer(learning_rate)
optimizer = tf.train.AdamOptimizer(learning_rate)
train_step = optimizer.minimize(cross_entropy)

init = tf.global_variables_initializer()
with tf.Session() as sess:
    # 初始化引數
    sess.run(init)
    # 定義批量大小和迭代次數
    batch_size = 9
    step = 1000
    # 開始訓練
    for i in range(step):
        # 獲取批量訓練的資料
        start = (i*batch_size) % dataset_size
        end = min(start+batch_size, dataset_size)
        # 輸入資料訓練
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 10 == 0:
            # 每10輪迭代獲取一次損失函式的值
            loss = sess.run(cross_entropy, feed_dict={x: X, y_: Y})
            # 輸出繪圖
            print(i, "epoch,loss:", loss)
            plt.plot(i, loss, 'ro')
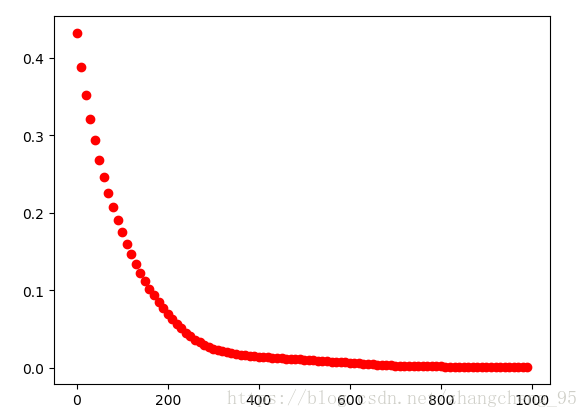
    plt.show()

實驗結果：

可以看到隨著迭代次數的增加，損失函式是逐漸減小的。

改進版：用函式來實現引數的定義，並加入L2正則，程式碼如下：

import tensorflow as tf
from numpy.random import RandomState
import matplotlib.pyplot as plt
# 隨機生成資料集，並自定義標籤
rdm = RandomState(1)
dataset_size = 128
X = rdm.rand(dataset_size, 2)
Y = [[int(x1+x2 < 1)] for (x1, x2) in X]


def get_weight(shape, lambd):
    # 生成一個變數
    var = tf.Variable(tf.random_normal(shape), dtype= tf.float32)
    # 將新生成變數的L2正則化損失加入集合
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambd)(var))
    return var


x = tf.placeholder(tf.float32, shape=[None, 2])
y_ = tf.placeholder(tf.float32, shape=[None, 1])

batch_size = 8
# 定義每一層網路中節點的個數
layer_dimension = [2, 10, 10, 1]
# 神經網路的層數
n_layers = len(layer_dimension)
# 維護前向傳播時最深層的節點，開始的時候就是輸入層
cur_layer = x
# 當前層的結點個數
in_dimension = layer_dimension[0]

for i in range(1, n_layers):
    # 下一層的節點數
    out_dimension = layer_dimension[i]
    # 生成當前層中的權重和偏置，並加入L2正則
    weight = get_weight([in_dimension, out_dimension], 0.001)
    bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
    cur_layer = tf.nn.relu(tf.matmul(cur_layer, weight) + bias)
    in_dimension = out_dimension

# 損失函式
mse_loss = tf.reduce_mean(tf.square(y_ - cur_layer))
tf.add_to_collection('losses', mse_loss)
loss = tf.add_n(tf.get_collection('losses'))

learning_rate = 0.001
optimizer = tf.train.AdamOptimizer(learning_rate)
train_step = optimizer.minimize(loss)
init = tf.global_variables_initializer()

with tf.Session() as sess:
    sess.run(init)
    for i in range(1000):
        start = (i * batch_size) % dataset_size
        end = min(start + batch_size, dataset_size)
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 10 == 0:
            l = sess.run(loss, feed_dict={x: X, y_: Y})
            print(i, "epoch,loss:", l)
            plt.plot(i, l, 'ro')
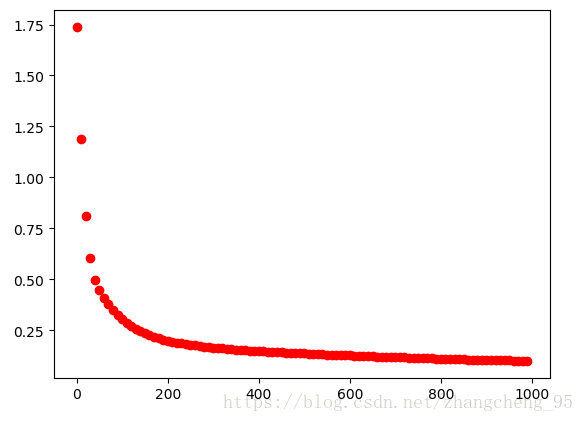
plt.show()

可以看到，由於加入了l2正則以避免過擬合，loss沒有之前訓練的那沒小