題目連結：http://poj.org/problem?id=1182

解題思路：

這道題是並查集題目中的經典。。。而且比普通並查集提高了一個檔次，下面在基礎並查集的前提上講解並查集的真正用法。

基礎回顧：

find()函式找根結點的兩種寫法如下：

第一種遞迴：

int find(int x)
{
	return x == pre[x] ? x : find(pre[x]);
}

第二種：

int find(int x)
{
	int root, temp;
	root = x;
	while(root != pre[root])
		root = pre[root];
	while(x != root)
	{
		temp = pre[x];
		pre[temp] = root;
		x = temp;
	}
	return root;
}
 

上面2種是最基本的查詢操作。

下面我們通過這道題來講解一下並查集的深層次應用。

輸入:動物個數n以及k句話,接著輸入k行,每一行形式為:d x y,在輸入時可以先判斷題目所說的條件2和3,即:
       1>若(x>n||y>n):即當前的話中x或y比n大,則假話數目sum加1.
       2>若(x==2&&x==y):即當前的話表示x吃x,則假話數目sum加1.

而不屬於這兩種情況外的話語要利用並查集進行判斷當前的話是否與此前已經說過的話相沖突.

struct node
{
	int parent;                     //p[i].parent表示節點i的父節點
	int relation;                   //p[i].relation表示節點i與其父節點(即p[i].parent)的關係
}p[50010];

  初始化函式為: 

void init(int n)
{
	int i;
	for(i = 1;i <= n; ++i)
	{
		p[i].parent = i;            //初始時集合編號就設定為自身
		p[i].relation = 0;        //因為p[i].parent=i,即節點i的父親節點就是自身,所以此時節點i與其父親節點的關係為同類(即p[i].relation=0)
	}
}
 

查詢操作：

合併操作：

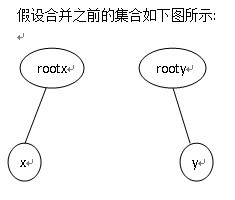
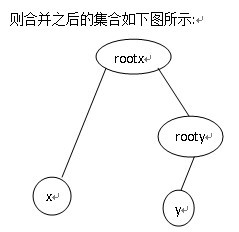
關係域更新：

當然，這道題理解到這裡思路已經基本明確了，剩下的就是如何實現，在實現過程中，我們發現，更新關係域是一個很頭疼的操作，網上各種分析都有，但是都是直接給出個公式，至於怎麼推出來的都是一筆帶過，讓我著實頭疼了很久，經過不斷的看discuss，終於明白了更新操作是通過什麼來實現的。下面講解一下

仔細再想想，rootx-x 、x-y、y-rooty，是不是很像向量形式?於是我們可以大膽的從向量入手：

tx       ty

|          |

x   ~    y

對於集合裡的任意兩個元素x，y而言，它們之間必定存在著某種聯絡，因為並查集中的元素均是有聯絡的（這點是並查集的實質，要深刻理解），否則也不會被合併到當前集合中。那麼我們就把這2個元素之間的關係量轉化為一個偏移量（大牛不愧為大牛！~YM）。

由上面可知：
x->y 偏移量0時 x和y同類

x->y 偏移量1時 x被y吃

x->y 偏移量2時 x吃y

有了這個假設，我們就可以在並查集中完成任意兩個元素之間的關係轉換了。

不妨繼續假設，x的當前集合根節點rootx，y的當前集合根節點rooty，x->y的偏移值為d-1（題中給出的詢問已知條件）

(1)如果rootx和rooty不相同，那麼我們把rooty合併到rootx上，並且更新relation關係域的值（注意：p[i].relation表示i的根結點到i的偏移量！！！！（向量方向性一定不能搞錯））

    此時 rootx->rooty = rootx->x + x->y + y->rooty，這一步就是大牛獨創的向量思維模式

    上式進一步轉化為：rootx->rooty = (relation[x]+d-1+3-relation[y])%3 = relation[rooty]，（模3是保證偏移量取值始終在[0,2]間）

(2)如果rootx和rooty相同(即x和y在已經在一個集合中，不需要合併操作了，根結點相同)，那麼我們就驗證x->y之間的偏移量是否與題中給出的d-1一致

    此時 x->y = x->rootx + rootx->y

    上式進一步轉化為：x->y = (3-relation[x]+relation[y])%3，
    若一致則為真，否則為假

最後總結一下：如果x,y不在一個集合裡面，說明他們之間還沒有構成任何關係，就需要把他們兩個合併，

如果x,y已經在一個集合裡面，說明他們之間已經構成了某種關係（同類，吃，被吃），然後用已經構建好的relation和輸入的d進行比較就行了，相等 就是真話，不相等就是假話。

分析到這裡，這道題已經從思想過渡到實現了。剩下的就是一些細節問題，自己處理一下就好了。

PS：做完這題，就可以去秒了大部分基礎的並查集了，嘿嘿

程式碼如下：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define Max 50010

struct node{
	int pre;
	int relation;
};
node p[Max];
int n,k;
	int d,a,b;
	int rootx,rooty;
	int sum=0;
int find(int x)
{
	int tmp = p[x].pre;
	if(x==tmp) return x;
	p[x].pre=find(tmp);
	p[x].relation=(p[x].relation+p[tmp].relation)%3;
	return p[x].pre;
}
void init()
{
	for(int i=0;i<Max;i++)
	{
		p[i].relation=0;
		p[i].pre = i;
	}
	sum=0;
}
void Union(int x,int y)
{
	p[rootx].pre = rooty;
	p[rootx].relation = (-p[x].relation+d-1+p[y].relation+3)%3;
}
int main()
{
	
	scanf("%d%d",&n,&k);
	init();
	while(k--)
	{
		scanf("%d%d%d",&d,&a,&b);
		if(a>n || b>n)
		{
			sum++;
			continue;
		}
		if(d==2 && (a==b))
		{
			sum++;
			continue;
		}
		rootx = find(a);
		rooty = find(b);
		if(rootx != rooty)
		{
			Union(a,b);
		}
		else
		{
			if(d==1) 
			{
				if(p[a].relation != p[b].relation)
				{
					sum++; 
					continue;
				}
				
			}
			if(d==2 && ((p[a].relation-p[b].relation+3)%3 !=d-1))
			{
				sum++;
				continue;
			}
		}
		
	}
	cout<<sum<<endl;
	return 0;
}

轉載連結：https://blog.csdn.net/niushuai666/article/details/6981689