A Primer on Trustworthy Secure Bootloading*

Secure bootloading is not very complicated, but we often make it seem complicated. In a discussion of this topic with colleagues, it was apparent that “secure boot” (also called “trusted”, “verified”, and “measured”, to list a few) was a vague and overloaded concept. In a way, a “let there be security!”
Commercially, secure bootloading often refers to a gatekeeping mechanism, whereby a trusted firmware prevents the computer from entering a useful state unless it is loading a pre-approved operating system (e.g. a kernel image signed by a Microsoft or another trusted vendor). Other interpretations exist with some better intentioned than others; it is not the goal of this manuscript to survey and critique existing work. The example in this work details a trustworthy secure-boot protocol designed to load any software, but also to authenticate the post-boot environment by endowing it with certified cryptographic keys unique to what was loaded. This allows an honest post-boot environment to prove its integrity to a trusted party, and to keep secure persistent state via encryption.
Defining our terms and aspirations
A secure bootloader seeks to bootstrap trust in a software environment, meaning to create certainty that the security properties we expect do indeed hold true. We consider trust to be binary (no such thing as trusting something only a little bit -- you either trust something or you don’t), but this can be refined: we can trust a software system’s integrity (meaning it is intact and unmodified, and matches a specific binary), but not the confidentiality (secrecy) of certain data it accesses. Likewise, we can describe a manufacturer as trusted to build a device according to a specification, but not trusted to keep cryptographic keys safe in perpetuity. If something can be authenticated (verified to match something expected), remote trust can be made conditional on integrity. If this is possible, trust is unconditional, and we just have to take it or leave it.
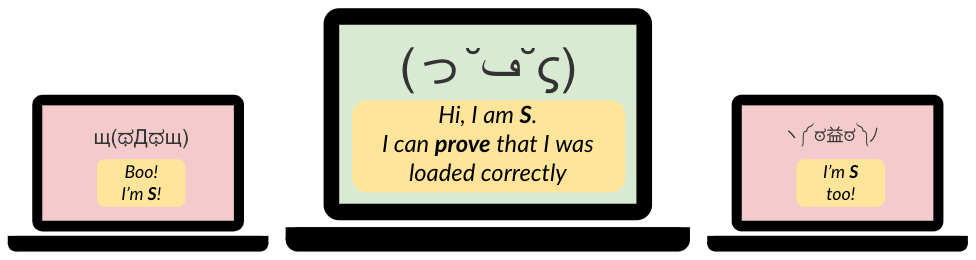
Our view of an idealized secure-boot protocol would allow one to load an arbitrary software environment (the post-boot environment) in a way that not only guarantees integrity, but also allows the software environment to convincingly prove its integrity (else how can we be sure that a secure boot was even performed?). Recall that we cannot achieve absolute security, but by making a few assumptions we can achieve this goal in practice.
In this work, I define secure bootloading to be a way to guarantee integrity of the (relatively large) initial state of a software system by leveraging existing unconditional trust in a (smaller) trusted computing base (TCB). This TCB consists here of everything that is able to observe or alter the function of our secure-boot protocol. This includes the essential hardware: CPU package, system memory modules, a read-only memory containing the bootloader program itself, and the wires connecting all of the above, but probably excludes any peripheral devices with no direct access to memory. The TCB is not limited to hardware, and our bootloader program must trust its own correctness because no part of the program can leak a secret or allow unexpected behavior to occur. While our secure-boot protocol seeks to convey trust in the system software it loads, we cannot create trust out of thin air and must begin with pre-existing, unconditional trust in a specific binary we expect to load. We can garner this trust through principled design, auditing, and perhaps even formal verification.
In order to communicate the integrity guarantee achieved during boot, the software environment will be given a set of unique, repeatable cryptographic keys and a certificate binding these keys to both the TCB and the specific post-boot environment. With this certificate, a remote first party can ① decide whether the certificate’s description of the post-boot environment is trustworthy and ② request a proof that a given software environment is indeed the one endorsed by the certificate. Without this proof the secure-boot protocol is somewhat meaningless, as there is no way to be sure it was performed at all, because an adversary could convince a user that any system is the secure system. The devil is in the details, so we cannot get much further without specifying a threat model to describe the space of malicious behavior our secure bootloader can tolerate.
Choosing a Threat Model
Alice wishes to send Bob a private letter, while Eve is very curious to find out what she would write. Alice trusts the post office to keep envelopes sealed, so Eve learns nothing. Actually, Eve learns nothing unless she shines a bright light through the envelope, or pretends to be Bob and opens his mail, or bribes the postal worker, or finds Alice’s letter in the trash after Bob has read it, or is clairvoyant and senses the message in some supernatural way. No system is secure unconditionally, and we must be thorough when setting the scene to describe a secure system to its intended users. A threat model contextualizes the security guarantees a system seeks to provide via a precise description of the entire space of malicious behavior the system can tolerate without compromising its guarantees. The threat model should also enumerate all trust assumed by the system, although this may be difficult to precisely state in the general case.
There are a number of parties with distinct incentives collaborating to create and use a system with a secure bootloader. These parties have varying degrees of access and distinct trust assumptions. If we were somehow able to trust in the integrity and availability of all parties involved, we would not have much need for a secure-boot protocol in the first place. A more interesting setting is one where we trust both the authentic hardware and its manufacturer and wish to bootstrap a trusted binary on that hardware in an untrusted setting. Below, we discuss some likely parties with access to a computer system to demonstrate the implications of access and trust on the security properties we can achieve.
Users of the system
Remote and unauthenticated (anonymous) users should be entirely untrusted by our secure-boot protocol. These include, for example, visitors to a website hosted by the system. They may, however, be able to cause the post-boot environment to perform specific tasks (serve pages of the above-mentioned website, or check a password as part of authentication, for example), so they may have some access to the system, and the secure-boot protocol must remain secure despite this access. If denial of service is also a concern, allowing untrusted users to cause the system to perform work is problematic in general.
Authenticated remote users may garner additional trust within the post-boot environment, as these are the parties able to get past a password prompt, and perhaps a second authentication factor. They have a pre-arranged relationship with the post-boot environment and may be granted more access than the anonymous unauthenticated users. If these users can provide inputs to the system, or if they can cause the system to store their data, the space of their possible interactions is not a small one. Can they cause the system to execute their code? Can they access any state that is not explicitly deemed to be public? Most importantly, are they able to learn the cryptographic keys sufficient to impersonate the certified post-boot environment on an untrusted machine?
Computer systems are constantly busy performing a diverse array of complicated tasks, and some of these can be misused for unintended behavior. Most software contains mistakes and some of which, if carefully abused, can allow the attacker to subvert access control, perform irreversible actions, and access secret information. In the case of our secure-boot protocol, the post-boot environment is assumed to be trusted (but authenticated) to maintain secrecy of its keys, meaning no untrusted party can learn the certified private key produced by the secure-boot protocol. It is entirely up to the post-boot environment to make wise choices regarding access granted to its users, and to guard against any leaks of the certified key.
Components of the post-boot software
In addition to the users of a system, we must consider trust in the components of the software system itself. Software is rarely written from scratch, and includes large libraries, frameworks, and other third-party components. Recall that the secure-boot protocol unconditionally trusts the desired post-boot binary to maintain secrecy of its unique private key. Without this confidentiality guarantee, integrity cannot be proven, and an adversary can impersonate a trusted post-boot environment. While a modern operating system offers some access control to protect confidentiality of information it manages, these systems are also enormous and far from perfect. The Linux kernel, for example, weighs in at some 12 million lines of code, making it a very problematic component to include in a TCB, as demonstrated by a trickle of reported vulnerabilities. Software modules, meanwhile, present additional challenges: these are written with different threat models in mind, by different parties with different incentives. For example, privileged modules added to the post-boot environment (such as a cloud operator’s proprietary drivers and management engines) have more or less unrestricted access to the post-boot environment, including its private key, and must be considered when describing the TCB.
In practice, any software allowed to execute in the post-boot environment, be it a driver, a binary from an app store, or JavaScript from a third-party advertisement fetched by visiting a web page, all have some access to the system. Trusting all software in the post-boot environment is extremely problematic; a trustworthy post-boot would do well to implement strong measures to minimize its own TCB.
The secure-boot protocol described in this work delegates the responsibility of safeguarding a post-boot environment’s private keys and assumes the post-boot software is made trustworthy. Existing work in the space of remotely attested execution (including my own work on the Sanctum Secure Processor) helps leverage this secure-boot protocol for a more holistic security argument by implementing fine-grained isolation of memory and computation.
The trusted computing base and physical access
The pre-boot environment software implements the secure-boot protocol and is necessarily trusted to correctly implement secure bootloading while safeguarding private information (the device’s private key). This software includes third-party library routines for cryptographic operations, which are trusted as well. In all, the pre-boot software is relatively small, and trust is not unreasonable (open source, audits, and formal verification are all viable here). The integrity of this trusted software, however, is also essential and must be guaranteed by the hardware in our TCB.
Given that we do not currently have a means to measure or inspect the hardware in order to authenticate it (although we can authenticate private data it has access to), we must trust its integrity. This is not insignificant given the reality of modern manufacturing and design: a computer processor system includes a huge diversity of third-party components essential to its function, many with some access to the system memory. The processor itself, as well as the memory devices, includes numerous third-party IP blocks for interfaces, clocking, power management, and other essential functions. The computer and its components are shipped between vendors and may be vulnerable to substitution or tampering. In addition to the manufacturer’s supply chain, any party with physical access to the system must also be considered capable of compromising the system’s integrity. The threat model for our secure-boot protocol described here excludes adversaries with physical access and trusts the manufacturer and their supply chain. Crucially, the manufacturer must safeguard their cryptographic keys, and the keys with which they provision each manufactured system.
The threat model for our secure-boot protocol
In order to be useful, a threat model must reflect the setting in which the system will operate. If a system’s threat model reads like a cheesy crime thriller novel in a setting lacking spies, secret factories, and nation-state budgets, it probably isn’t an appropriate one to underpin a productive security argument. Instead, the threat model should help users correctly use the system to achieve the security guarantees relevant to its intended application. Are the trusted parties trustworthy in the system’s application? Is the system guarding less value than the likely cost of an attack by the modeled adversary?
The secure-boot protocol described in this work excludes adversaries with physical access and trusts the manufacturer and their supply chain to correctly implement the TCB hardware (no sneaky back doors) and software (secure bootloader is correctly implemented). Crucially, the manufacturer must safeguard their cryptographic keys, and the keys with which they provision each manufactured system (no selling insecure emulators that convincingly pretend to be secure hardware). We expect our secure boot is performed in an untrusted setting, and assume the adversary is able to boot an alternate, malicious binary on the system and interact with it (but not alter the function of the hardware or extract its secret key). We assume unconditional trust in the honest binary we intend to securely load, and in particular assume secrecy of the binary’s cryptographic keys. We also trust in the security properties offered by the various cryptographic primitives the secure-boot protocol relies on. A trusted first party (user seeking to bootstrap a trusted software) specifies a binary to load, and later performs attestation to bootstrap trust in the system.
A quick primer on relevant cryptographic primitives
In addition to the authority of the TCB to supply the secure bootloader program and control access to keys, our protocol relies on some cryptography to convey trust and construct proofs. The security properties offered by the cryptographic primitives are assumed to hold, and we must take care to choose appropriately large keys. Below is a brief introduction to the cryptographic primitives used in this article, including references to their portable C implementation, and a discussion of key strength.
I assume the reader has rudimentary familiarity with the concept of encryption, and believes my claim that a shared secret can allow for communication with guarantees of confidentiality and integrity of messages for the parties holding a shared secret.
Hashes for measurement and commitment
Imagine a system that, given an input, looks up the corresponding output in a large book, amending the book for each new input by flipping, say, 512 coins and recording the outcome. The chance of two inputs producing the same output (a collision) is vanishingly small (0.5⁵¹², for a fair coin). So small, in fact, that we can be reasonably certain no such event will ever be observed. This hypothetical system is a random oracle. A cryptographic hash is a deterministic one-way function that approximates a random oracle; cryptographic hashes have a wealth of useful properties, of which we will primarily rely on collision resistance (finding two inputs that produce the same output is extremely difficult) and preimage resistance (finding an input that produces a given hash is also infeasible).
Collision and preimage resistance are extremely useful for cryptographic measurement: arbitrarily large data structures can be hashed to produce a compact, unique (with high probability) value, making remote comparison of large data structures simple. Furthermore, fooling this comparison within the protocol is infeasible, as finding another data structure with the a given hash is extremely difficult. The probability of collision (finding any two data structures with the same hash) is vanishingly small, so in practice a cryptographic hash uniquely describes (measures) the data it was computed from. In the case of our secure-boot protocol, a cryptographic hash measures the software image being loaded and allows the trusted first party to authenticate the post-boot environment.
The same properties make cryptographic hash functions useful for commitment. Consider a hypothetical scenario where Alice and Bob are invited to bid on building a bridge for their local transportation department. The department is required to accept the lowest bid, creating perverse incentives for contractors to marginally underbid others, an opportunity for corruption, and an advantage for contractors that bid last (if the bids are not kept private). A cryptographic commitment scheme can help. Alice and Bob commit to their bids by hashing their (salted) bids and announcing the result, which does not reveal their bids. After all contractors announced their commitments, they reveal their bids, and the lowest is hired. The contractors cannot lie about their bids, as the properties of the cryptographic hash prevent them from inventing another bid with the same hash. Commitments are tremendously useful for promising certain data without revealing it.
/* sha3/sha3.h */
void sha3( uint8_t* in, // What are we hashing? size_t in_size, // How large is the input, in Bytes? uint8_t* out_hash, // Where should the hash output go? int hash_bytes ); // 64 for a 512-bit hash.
/* The hash can also be extended, allowing it to be computed from multiple input, instead of a one-shot function above: */
typedef sha3_ctx_t; // intermediate values for sha3
int sha3_init( sha3_ctx_t* scratchpad, int hash_bytes );
int sha3_update( sha3_ctx_t* scratchpad, uint8_t* in, size_t in_size );
int sha3_final( uint8_t* out_hash, sha3_ctx_t* scratchpad );
In this work, we use the SHA-3 hash (via the interfaces described above) due to its flexibility, small implementation size (this work uses this portable C implementation), and robustness at the time of this publication. A diverse array of other hash functions exist with a variety of quirks and features. Some offer stronger guarantees than others: SHA-1, for example, is no longer recommended despite widespread adoption because a trickle of weaknesses have been demonstrated since 2005. At the time of this writing, attacking a SHA-1 hash is no longer considered computationally infeasible.
Public-Key Cryptography, Signatures, and Certificates
Unlike conventional encryption (with symmetric ciphers), which uses a key (password) to encrypt and decrypt a message, public-key cryptography uses distinct keys for encryption and decryption. The two keys are generated as a pair and one does not help an adversary discover the other. Conventionally, one of the keys is kept secret (and is called a secret or private key) and the other made public (the public key). If Alice knows Bob’s public key and wishes to send him a secret message, she can encrypt a message for Bob without having a pre-arranged shared secret. Eve can also encrypt messages for Bob, if she knows the public key, but cannot read Alice’s.
Public-key cryptography is essential for implementing signatures, whereby a party encrypts a measurement of a message with their private key, allowing anyone in possession of their public key to verify it by decrypting, re-computing the measurement, and ensuring the measurements match. This signature includes both the message and the encrypted hash. This signature is a commitment and serves as irrevocable proof that the party has seen the signed message.
A specific and useful application of cryptographic signatures is in issuing certificates for cryptographic keys in order to endorse them as trustworthy. A certificate is simply a signature of a public key (and additional relevant information, such as a description of the system to which the public key belongs). In our example, the manufacturer certifies the public key of each TCB it manufactures, allowing the device to prove its trusted origin as long as it can maintain secrecy of its private key. Likewise, the secure-boot protocol creates a certificate for the post-boot environment’s public key, described by a hash of the post-boot environment.
/* ed25519/ed25519.h */
/* The key derivation function creates a key pair from a 32-Byte "seed" value: */void ed25519_create_keypair( uint8_t[32] out_pk, // Public key uint8_t[64] out_sk, // Secret key uint8_t[32] in_seed ); // entropy
/* The signing routine computes a 64-Byte signature from an arbitrary message with a given key pair: */void ed25519_sign( uint8_t[64] out_signature, uint8_t* message, size_t message_size, uint8_t[32] pk, uint8_t[64] sk );
/* The verification routine checks whether a signature corresponds to a given message and public key: */bool ed25519_verify( uint8_t[64] signature, uint8_t* message, size_t message_size, uint8_t[32] pk);
While many public-key cryptosystems exist, our secure bootloader employs ed25519 elliptic curve cryptography (via the routines described above) for its small keys, permissive license, and efficient key derivation. We modify a portable C implementation of ed25519 signatures and key derivation to use SHA-3 hashes in place of the original implementation’s use of SHA256, and make the resulting library freely available as well.
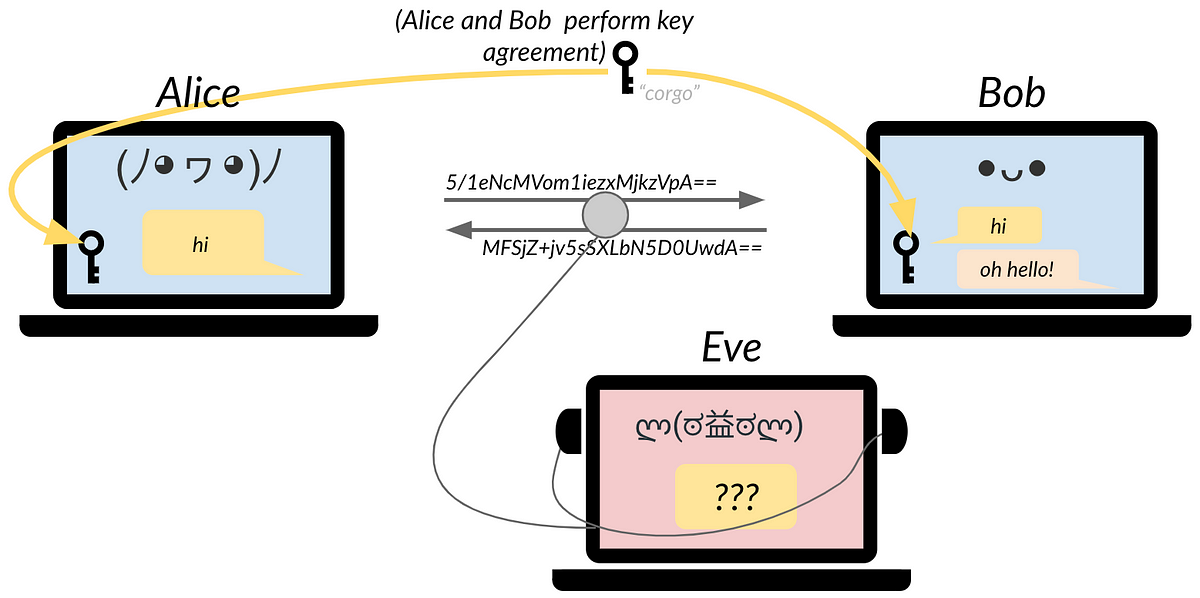
Key agreement for sharing secrets in an untrusted setting
In order to send secrets privately and with integrity, communicating parties can employ basic cryptography. The communicating parties, Alice and Bob, employ a key agreement protocol in order to establish a shared secret with which to perform a cryptographic protocol. If key agreement is performed correctly, a hypothetical adversary Eve learns nothing about the shared secret even if she is able to inspect Alice’s and Bob’s messages.
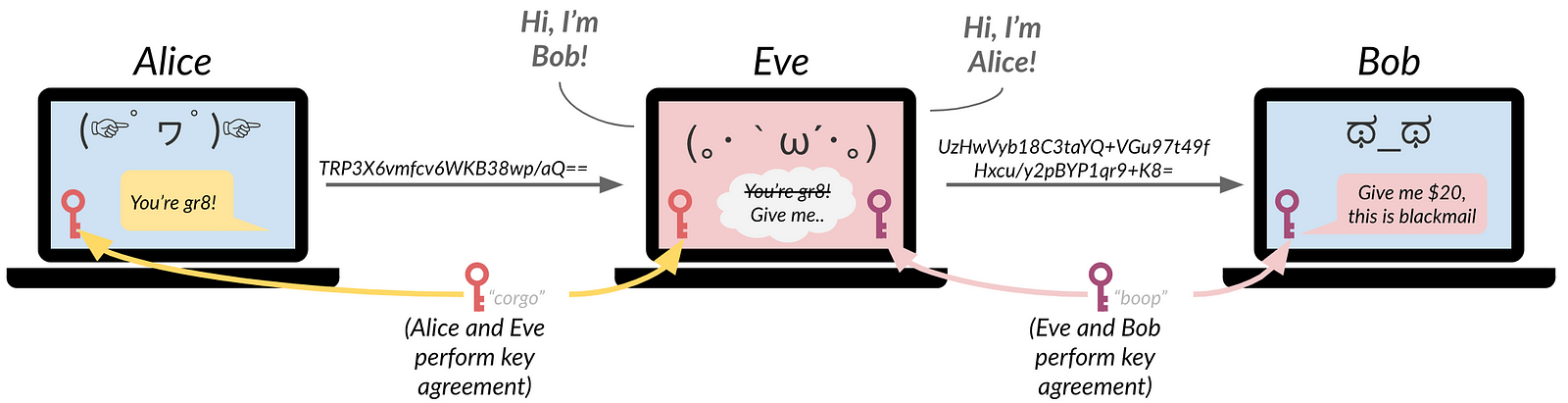
A sneaky complication occurs when Eve is able to intercept and substitute Alice’s and Bob’s messages, inserting herself in the middle of their communication. In this case, she is a man-in-the-middle (MITM) adversary, and can claim she is Bob to Alice, and Alice to Bob. She can perform separate key agreement with each and proxy their messages. In this scenario, Alice and Bob have neither secrecy nor integrity guarantees from Eve. They may not realize this unless they authenticate one another, such as by signing the agreed upon shared key with their well-known public keys.

/* ed25519/ed25519.h */
/* A key agreement routine, whereby A's public key and B's secret key yield the same shared secret as B's public key and A's secret key: */void ed25519_key_exchange( uint8_t[32] out_shared_secret, uint8_t[32] pk_a, uint8_t[64] sk_b );
Conveniently, the ed25519 elliptic curve library introduced earlier also implements key agreement (via the routine shown above): deriving a shared secret from a secret key and another key pair’s public key. The useful property here is that for parties A and B with keys {pk_a, sk_a}and {pk_b, sk_b}, the same shared key k is found byed25519_key_exchange(&k, pk_b, sk_a) and ed25519_key_exchange(&k, pk_a, sk_b). As a result, since only A and B are trusted to have sk_a andsk_b respectively, only A and B can derive k — key agreement.
Selecting appropriate key sizes
The cryptographic primitives described above rely on strong keys to prevent an attacker from subverting the security of these cryptosystems. When combining cryptosystems, as is the case in our secure-boot protocol, mismatched key strengths across cryptographic primitives are problematic, as the security of a system may reduce to its weakest key, and memory and computational resources are wasted handling larger keys elsewhere. The inputs to key derivation routines are also important: creating large, strong keys from a small seed value is inadvisable, as an attacker may be able to enumerate a small space of generated keys despite the keys themselves being large. A trusted system must size its keys correctly in order to remain secure as an attacker’s toolkit and budget grows over the system’s lifetime.
Estimating the strength of a cryptosystem based on the size of a key is difficult and requires expertise in both cryptography and the tools available to attack cryptosystems. Luckily, this is a broadly valuable estimate and expert opinions are readily available. In the US, the National Institute for Standards and Technology (NIST) publishes detailed guidelines for key sizes to be used by new designs with various classes of cryptographic systems. Other agencies around the world release similar guidelines. The 256-bit seed required to generate keys for our chosen public-key cryptosystem (ed25519, an elliptic curve system) is considered trustworthy by NIST through 2030 and beyond. A comparison of recommendations from other agencies generally agrees. The same recommendations show 256-bit hashes are sufficient with ed25519’s 64-Byte elliptic curve keys, validating the use of SHA-3–256 and SHA-3–512 by our secure-boot protocol.
A Step-by-Step guide to Securely Booting a RISC-V Rocket
You are a humble manufacturer M of a trusted processor D built with the RISC-V Rocket ecosystem. These processors are untethered (do not require a trusted host computer to be booted) and have a small non-volatile boot ROM from which execution begins at reset. You wish to load a software boot image S from an external device via a boot program. All accesses to memory are performed by the processor (no direct memory access by devices, or at least DMA can be prohibited for some addresses). You are ready to implement a trusted boot (exemplified in its entirety via [1][2] with the MIT Sanctum bootloader) for your computer system by following the steps below:
1. Be a trustworthy certificate authority
As mentioned before, the security of the secure-boot protocol is rooted in a manufacturer’s private key. Specifically, we place the manufacturer in the role of a certificate authority: M has keys (PKm, SKm). PKm is widely known, while SKm remains a well-guarded secret with the manufacturer. The security of the entire secure-boot ecosystem hinges unconditional trust in M’s ability to safeguard SKm, as this is M’s means of certifying the trustworthy origin of any hardware they manufacture. Should SKm be compromised, an adversary would be able to convince a user that any system, such as an insecure emulator, is a trustworthy one.
Also previously stated, we employ ed25519 public-key cryptography (portably implemented here), although RSA or any other public-key cryptosystem is viable, threat model permitting. The general problem of constructing a robust public-key infrastructure is very much an open one, so the M must broadcast PKm in some unspecified trustworthy way — a reasonable demand given its prevalence in web security.
A segment of C code to exemplify the generation of (PKm, SKm), or any other ed25519 key pair is given below (and in a gist). This code assumes a trustworthy execution environment under M’s stringent control, and utilizes the ed25519 library introduced above.
#include <ed25519/ed25519.h>
uint8_t pk[32];uint8_t sk[64];
/* This seed is as valuable as the secret key! */uint8_t secret_entropy[32];
/* NOTE: we assume some application-dependent source of trusted entropy */get_trusted_entropy(secret_entropy, 32);
ed25519_create_keypair(pk, sk, secret_entropy);
2. Endow each system with a unique cryptographic key
In addition to correctly designing and manufacturing the processor system, M must provision each TCB with a unique key pair (PKd, SKd) in some unspecified but trustworthy way. These keys must be available to the trusted secure-boot implementation, but SKd must not be available to any other software (the post-boot environment). To this end, we assume a special application programming interface (API) by which the processor system retrieves its secret key:
void get_sk_d(uint8_t[64] out_sk_d);/* Accessor for the device key SKd populates the buffer out_sk_d with the key unless `hide_sk_t_until_reboot` has previously been invoked. */
void hide_sk_d_until_reboot();/* Ensures that subsequent calls to `get_sk_d` do not yield any information about SKd until the system restarts. */
Threat model permitting, it would be reasonable to store SKd in on-chip non-volatile memory, and rely on the boot software to disable access to the key in the post-boot environment. More resilient key derivation, such as recovering the key from a physical unclonable function (PUF) at boot are also attractive.
3. Certify the public key of each manufactured system
In order to communicate that PKd corresponds to a computer with a trustworthy TCB, M certifies it by computing a signature of PKd with SKm. The certificate is an endorsement of D by M, which conveys a proof that the trusted M manufactured D (this can be strengthened by a certificate transparency scheme), meaning D is trusted to correctly implement the TCB including a secure-boot protocol, and SKm is not known to any adversary, while PKd is unique.
The following C code (also given by this gist) shows how PKd may be certified by M at the time of D’s manufacture. This code assumes a trustworthy execution environment under M’s stringent control:
#include <ed25519/ed25519.h>
/* The unique public key assigned by M to one of the devices it has manufactured. */extern uint8_t pk_d[64];
extern uint8_t pk_m[32];extern uint8_t sk_m[64]; /* Extremely sensitive information! */
/* The endorsement. */extern uint8_t out_pk_d_sig[64];
/* Compute the endorsement of PKd by M */ed25519_sign(out_pk_d_sig, pk_d, 32, pk_m, sk_m);
4. Execute from a trusted ROM at reset, and clear memory
First-instruction integrity is essential for secure boot: even a single instruction from an untrusted source can create attacker-specified behavior and void any guarantees our system may aspire to offer.
Fortunately, this is a straightforwardly solved problem in an untethered RISC-V Rocket. The processor cores are wired to execute at address 0x1000 at reset, which can correspond to a trusted ROM (a read-only memory and a part of the TCB). Via the code in this trusted ROM, the unmodified RISC-V rocket initializes memory with a software image, sets registers to known values, and transfers control to S in system memory. Our secure-boot protocol extends the boot ROM to perform a few additional operations described in subsequent steps, in order to set up the following memory layout:
