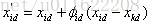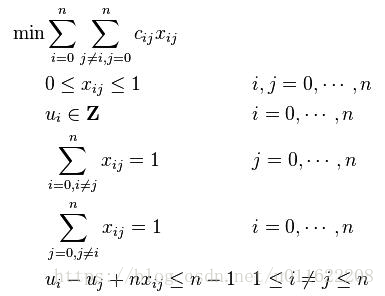人工蜂群演算法求解TSP問題
阿新 • • 發佈:2018-12-28
人工蜂群演算法求解TSP問題
【標籤】 ABC TSP Matlab
data:2018-10-19 author:怡寶2號
【總起】利用人工蜂群演算法(Artificial Bee Colony Algorithm, 簡稱ABC演算法)求解TSP問題,語言:matlab
1. 演算法簡介
人工蜂群演算法(Artificial Bee Colony Algorithm, 簡稱ABC演算法)是一個由蜂群行為啟發的演算法,在2005年由Karaboga小組為優化代數問題而提出。其主要是為了解決多變數函式優化問題。
2. 演算法原理
標準的ABC演算法通過模擬實際蜜蜂的採蜜機制將人工蜂群分為3類: 採蜜蜂、觀察蜂和偵察蜂。整個蜂群的目標是尋找花蜜量最大的蜜源。在標準的ABC演算法中,採蜜蜂利用先前的蜜源資訊尋找新的蜜源並與觀察蜂分享蜜源資訊;觀察蜂在蜂房中等待並依據採蜜蜂分享的資訊尋找新的蜜源;偵查蜂的任務是尋找一個新的有價值的蜜源,它們在蜂房附近隨機地尋找蜜源。所以演算法總體分為3個部分。
假設問題的解空間是D維的,採蜜蜂與觀察蜂的個數都是S,採蜜蜂的個數或觀察蜂的個數與蜜源的數量相等。則標準的ABC演算法將優化問題的求解過程看成是在D維搜尋空間中進行搜尋。每個蜜源的位置代表問題的一個可能解,蜜源的花蜜量對應於相應的解的適應度。一個採蜜蜂與一個蜜源是相對應的。與第i個蜜源相對應的採蜜蜂依據如下公式尋找新的蜜源:
其中,i=1,2,···,S,表示蜜源、採蜜蜂、觀察蜂的個數,D=1,2,···,D,表示優化變數的個數。Φid為[-1,1]之間的隨機數,k≠i。
將新生成的可能解{Xi1’,Xi2’,···,XiD’}與原來的解{Xi1,Xi2,···,XiD}做比較,採用貪婪選擇策略保留較好的解。
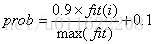
對每個採蜜蜂按上式對每個採蜜蜂計算一個概率。觀察蜂以上面計算的概率接受採蜜蜂,並利用採蜜蜂更新的公式進行更新,再進行貪婪選擇。
當所有的採蜜蜂和觀察蜂都搜尋完整個搜尋空間時,如果一個蜜源的適應值在給定的步驟內(定義為控制引數“limit”) 沒有被提高, 則丟棄該蜜源,而與該蜜源相對應的採蜜蜂變成偵查蜂,偵查蜂通過已下公式搜尋新的可能解。
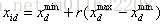
[xdmin]: https://img-blog.csdn.net/201810191750084?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTE2MjIyMDg=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70
其中,r是[0,1]的隨機數,xmin和xmax是第d個變數空間的下界和上界。
3. 模型
TSP問題,就是從一個點出發,再回到出發點,要求整個的最短路線。具體數學公式如下:
4. 總結
- 人工蜂群演算法主要分:採蜜、觀察、偵察三個階段;
- 整個原理和遺傳演算法的原理很類似,採蜜蜂就相當於初始化父代chrom,觀察蜂相當於輪盤賭選擇之後的子代,偵察蜂就是在limit次中沒能找到更優秀的解時,捨棄該解,再隨機初始化。
5. 程式和結果
% 人工蜂群演算法求解TSP問題
% 引數:
% 輸出:
%
% 有問題詳諮詢:[email protected]
% (有償代寫程式)close allclc
% 人工蜂群演算法求解TSP問題
% 引數:
% 輸出:
%
% 有問題詳諮詢:[email protected](有償代寫程式)
close all
clc
%% 引數初始化
parameter = initial();
%% 畫初始路徑圖
initialDraw(parameter);
runtime=10; %通過修改runtime的值,改變程式的執行次數,用以演算法的健壯性
GlobalMins=zeros(1,runtime);
for r=1:runtime
%初始化種群
% for i =1:FoodNumber
Foods = initial(runtime,NC);
% end
%計算適應度函式值
for i=1:FoodNumber
route=Foods(i,:);
Fitness(i)=calculateFitness1(route);
end
%% 初始化搜尋次數,用於和Limit比較
trial=zeros(1,FoodNumber);
%找出適應度函式值的最小值
BestInd=find(Fitness==min(Fitness));
BestInd=BestInd(end); %避免有兩個相同的位置,只取其一
GlobalMin=Fitness(BestInd);
GlobalParams=Foods(BestInd,:);
%迭代開始
iter=1; %初始化迭代次數
j=1; %用以初始化結果
while((iter<=maxCycle))
%%%%%% 採蜜蜂模式 %%%%%%
for i=1:FoodNumber
%計算新蜜源的適應度函式值
FitnessSol=calculateFitness1(route_next);
%使用貪婪準則,尋找最優蜜源
if (FitnessSol<Fitness(i)) %若找到更好的蜜源,搜尋次數清零
Foods(i,:)=route_next;
Fitness(i)=FitnessSol;
trial(i)=0;
else
trial(i)=trial(i)+1; %超過設定的Limit次,則該蜂成為偵察蜂
end;
end;
%%%%%% 根據適應度值計算彩蜜蜂被跟隨的概率 %%%%%%
prob=(0.9.*Fitness./max(Fitness))+0.1;
%%%%%% 觀察蜂 %%%%%%
i=1; %要跟隨的採蜜蜂
t=0; %標記觀察蜂
while(t<FoodNumber)
if (rand<prob(i)) %按概率選擇要跟隨的採蜜蜂
t=t+1;
%計算新蜜源的適應度函式值
FitnessSol=calculateFitness1(route_next);
%使用貪婪準則,尋找最優蜜源
if (FitnessSol<Fitness(i))%若找到更好的蜜源,搜尋次數清零
Foods(i,:)=route_next;
Fitness(i)=FitnessSol;
trial(i)=0;
else
trial(i)=trial(i)+1;%超過設定的Limit次,則該蜂成為偵察蜂
end
end
i=i+1; %要跟隨的下一個採蜜蜂
if (i==(FoodNumber)+1)
i=1;
end
end
% 記錄此時更好的解
ind=find(Fitness==min(Fitness));
ind=ind(end);
if (Fitness(ind)<GlobalMin)
GlobalMin=Fitness(ind);
GlobalParams=Foods(ind,:);
end
%%%%%% 偵查蜂模式 %%%%%%
ind=find(trial==max(trial));
ind=ind(end);
if (trial(ind)>Limit) %若搜尋次數超過極限值,則進行隨機搜尋產生新解
FitnessSol=calculateFitness1(route_new);
Foods(ind,:)=route_new;
Fitness(ind)=FitnessSol;
end
%%%%%% 建立一個次數和最優的矩陣,以便於畫圖 %%%%%%
Cishu(j)=iter; %迭代次數行向量
zuiyou(j)=GlobalMin; %每次迭代得到的最優解
j=j+1;
iter=iter+1;
end % while(iter<=maxClcle)
GlobalMins(r)=GlobalMin; %程式執行完一次,記錄這次的最優路徑長度
disp(['第',num2str(r),'次執行得到的最優路徑是:',num2str(GlobalParams),',此條路徑的長度是:',num2str(GlobalMins(r))])
end %end of runs
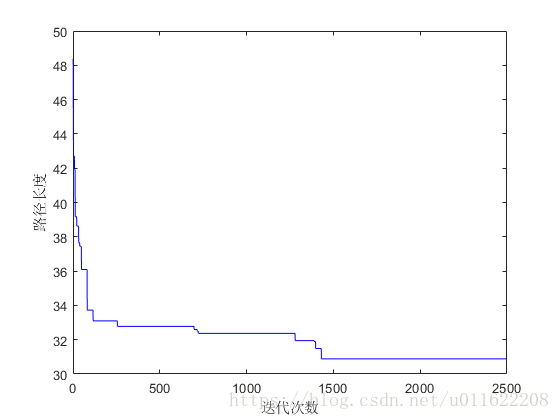
%%%%%% 畫曲線圖 %%%%%%
figure(2);
plot(Cishu,zuiyou,'b');
%title('優化曲線');
xlabel('迭代次數');
ylabel('路徑長度');
figure(3);
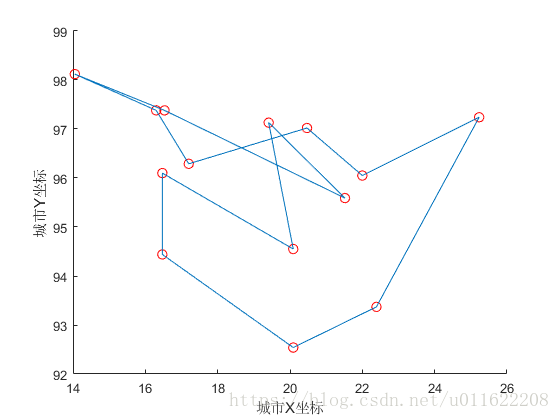
%%畫出優化路徑圖
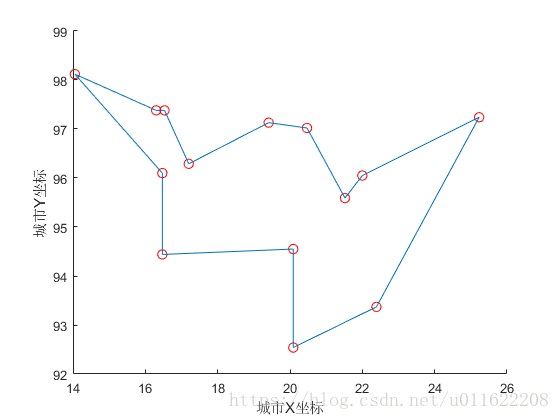
finalDraw(GlobalMin, parameter)
結果: