用遺傳演算法求解TSP問題
遺傳演算法簡介
關於遺傳演算法,首先看一段維基百科的解釋:
遺傳演算法是模仿自然界生物進化機制發展起來的隨機全域性搜尋和優化方法,它借鑑了達爾文的進化論和孟德爾的遺傳學說。其本質是一種高效、並行、全域性搜尋的方法,它能在搜尋過程中自動獲取和積累有關搜尋空間的知識,並自適應的控制搜尋過程以求得最優解。遺傳演算法操作使用適者生存的原則,在潛在的解決方案種群中逐次產生一個近似最優解的方案,在遺傳演算法的每一代中,根據個體在問題域中的適應度值和從自然遺傳學中借鑑來的再造方法進行個體選擇,產生一個新的近似解。這個過程導致種群中個體的進化,得到的新個體比原來個體更能適應環境,就像自然界中的改造一樣。
遺傳演算法是電腦科學人工智慧領域中用於解決最優化的一種搜尋啟發式演算法,是進化演算法的一種。這種啟發式通常用來生成有用的解決方案來優化和搜尋問題。進化演算法最初是借鑑了進化生物學中的一些現象而發展起來的,這些現象包括遺傳、突變、自然選擇以及雜交等。
概括來說遺傳演算法:
- 模仿生物進化。
- 可以找到一個近似最優解(不一定是全域性最優解)。
- 是電腦科學人工智慧的一種演算法。
遺傳演算法的基本步驟是:
- 初始化。隨機選擇一些個體組成最初的種群(Population),地球最原始的生命也是隨機產生的。
- 評估。通過某種方法來評估個體的適應度。個體的生存能力。
- 選擇。類似於自然選擇,優良的基因(Gene)、生存能力強的被選擇下來的概率要大。當然,也存在屌絲逆襲的情況。
- 交叉。產生後代,基因交叉,可以理解為有性繁殖,子代會分別從父母那得到部分基因。
- 變異。後代的基因可能會變異。變異在生物進化起了很大作用。
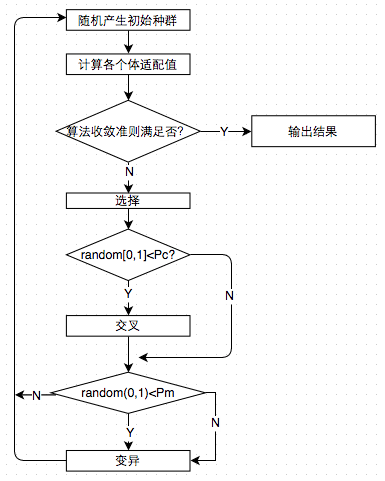
3-5步是產生新種群的步驟,新群體再進行評估,然後再選擇、交叉、變異,一直迴圈2-5步,最終找到一個近似最優解。遺傳演算法的流程圖如下;
TSP問題簡介
TSP問題全稱旅行商問題(Traveling Salesman Problem,TSP),別名旅行推銷員問題、貨郎擔問題,與哈密頓迴路問題有密切聯絡。且看維基百科的解釋:
旅行推銷員問題(Travelling Salesman Problem,又稱為旅行商問題、貨郎擔問題、TSP問題)是一個多區域性最優的最優化問題:有n個城市,一個推銷員要從其中某一個城市出發,唯一走遍所有的城市,再回到他出發的城市,求最短的路線。也即求一個最短的哈密頓迴路。
C-TSP問題就是中國旅行商問題(China Traveling Salesman Problem),求解中國34個一線城市的最優路線。給出中國34個城市的經緯度:
| 編號 | 城市名 | 東經 | 北緯 | 編號 | 城市名 | 東經 | 北緯 |
|---|---|---|---|---|---|---|---|
| 1 | 北京 | 116.46 | 39.92 | 18 | 南京 | 118.78 | 32.04 |
| 2 | 天津 | 117.2 | 39.13 | 19 | 合肥 | 117.27 | 31.86 |
| 3 | 上海 | 121.48 | 31.22 | 20 | 杭州 | 120.19 | 30.26 |
| 4 | 重慶 | 106.54 | 29.59 | 21 | 福州 | 119.3 | 26.08 |
| 5 | 拉薩 | 91.11 | 29.97 | 22 | 南昌 | 115.89 | 28.68 |
| 6 | 烏魯木齊 | 87.68 | 43.77 | 23 | 長沙 | 113 | 28.21 |
| 7 | 銀川 | 106.27 | 38.47 | 24 | 武漢 | 114.31 | 30.52 |
| 8 | 呼和浩特 | 111.65 | 40.82 | 25 | 廣州 | 113.23 | 23.16 |
| 9 | 南寧 | 108.33 | 22.84 | 26 | 臺北 | 121.5 | 25.05 |
| 10 | 哈爾濱 | 126.63 | 45.75 | 27 | 海口 | 110.35 | 20.02 |
| 11 | 長春 | 125.35 | 43.88 | 28 | 蘭州 | 103.73 | 36.03 |
| 12 | 瀋陽 | 123.38 | 41.8 | 29 | 西安 | 108.95 | 34.27 |
| 13 | 石家莊 | 114.48 | 38.03 | 30 | 成都 | 104.06 | 30.67 |
| 14 | 太原 | 112.53 | 37.87 | 31 | 貴陽 | 106.71 | 26.57 |
| 15 | 西寧 | 101.74 | 36.56 | 32 | 昆明 | 102.73 | 25.04 |
| 16 | 濟南 | 117 | 36.65 | 33 | 香港 | 114.1 | 22.2 |
| 17 | 鄭州 | 113.6 | 34.76 | 34 | 澳門 | 113.33 | 22.13 |
遺傳演算法應用於TSP問題
基因編碼
n個城市的的基因編碼方式為:
- 給每一個城市一個序號,如1->北京,2->上海,3->廣州,。。。。,n->成都。
- 用包含n個城市的序號的陣列序列表示一種路線(個體),陣列元素的序號表示旅行的順序,如{3, 1, 2,。。。。,n}表示的旅行順序為:廣州->北京->上海->。。。。->成都。
- 數值序列中值不重複,即每個城市只去一次。
初始化種群
隨機生成m個基因編碼序列作為初始種群。
評估適應度
TSP問題中路線越短越好,適應度取值為總距離的倒數,即1/distance。
產生新種群
產生新種群分為選擇、交叉和變異。個體被選中的概率取決於該個體的適應度值,比如有5個個體,他們的適應度值為:
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 0.3 | 0.2 | 0.1 | 0.4 | 0.8 |
在[0.0, 1.8)隨機產生一個浮點數,如0.8,則4號個體被選中。
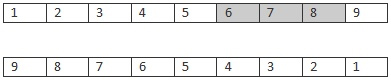
隨機選擇兩個個體後,以概率Pc交叉,子代分別繼承父母的部分基因,且保持順序與父代一致,如父代的基因序列:
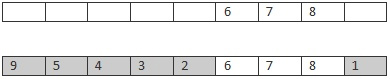
隨機選取Parent1的部分基因,如678,與Parent2交叉,結果如下:
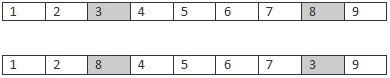
交叉完後就是變異,變異以Pm的概率發生。在TSP問題中因為每個城市只經過一次,所以在變異的時候不能只是改變基因序列中的某一位的值(這會導致一個城市經過兩次),應該隨機交換兩個位置的值,如:
交換了3和8的位置。
實現程式碼
參考了用遺傳演算法解旅行商問題的程式碼,也是用Python實現的,總共有4個檔案:
- Life.py。個體類。
- GA.py。遺傳演算法類。
- TSP_GA.py。TSP問題,命令列。
- TSP_GA_w.py。TSP問題,圖形介面模擬。
其中TSP_GA_w.py是在TSP_GA.py增加了一個圖形介面,以比較直觀地方式來看結果。TSP_GA_w.py和TSP_GA.py任選一個執行即可。
關鍵程式碼說明
GA.py中實現遺傳演算法的核心程式碼如下:
def next(self):
"""產生下一代"""
self.judge()
newLives = []
newLives.append(self.best)
while len(newLives) < self.lifeCount:
newLives.append(self.newChild())
self.lives = newLives
self.generation += 1
def judge(self):
"""評估,計算每一個個體的適配值"""
self.bounds = 0.0 #適配值之和,用於選擇是計算概率
self.best = self.lives[0] #儲存這一代中最好的個體
for life in self.lives:
life.score = self.matchFun(life)
self.bounds += life.score
if self.best.score < life.score:
self.best = life
def newChild(self):
"""產生新後代"""
parent1 = self.getOne()
rate = random.random()
#按概率交叉
if rate < self.croessRate:
#交叉
parent2 = self.getOne()
gene = self.cross(parent1, parent2)
else:
gene = parent1.gene
#按概率突變
rate = random.random()
if rate < self.mutationRate:
gene = self.mutation(gene)
return Life(gene)
def cross(self, parent1, parent2):
"""交叉"""
index1 = random.randint(0, self.geneLenght - 1)
index2 = random.randint(index1, self.geneLenght - 1)
tempGene = parent2.gene[index1:index2] #交叉的基因片段
newGene = []
p1len = 0
for g in parent1.gene:
if p1len == index1:
newGene.extend(tempGene) #插入基因片段
p1len += 1
if g not in tempGene:
newGene.append(g)
p1len += 1
self.crossCount += 1
return newGene以下是執行中的部分截圖:
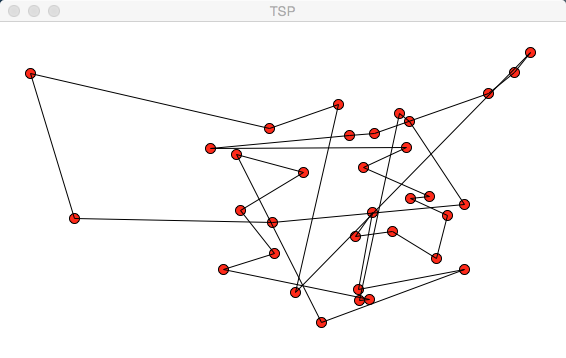
初始情況:
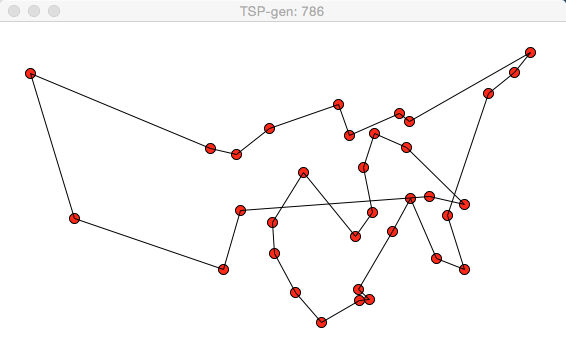
786代的情況:
可以看出,結果比最初情況要好。
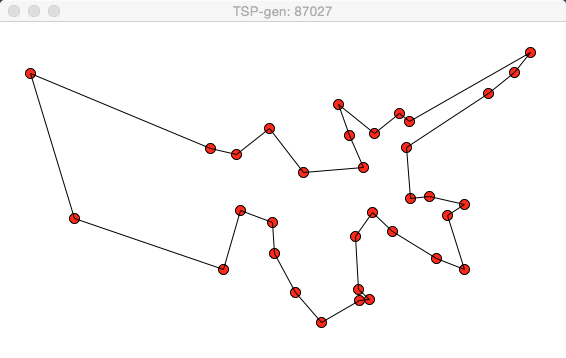
趨於穩定的情況:
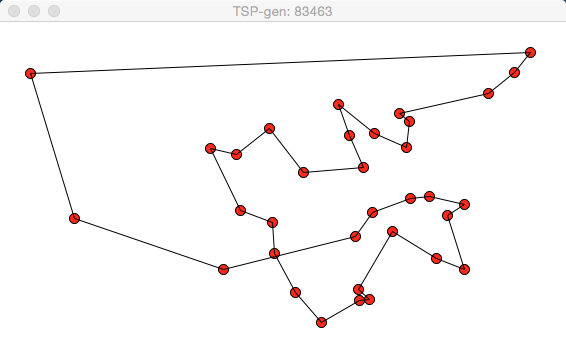
另一個趨於穩定的情況:
從圖中可看出,結果在向最優解發展。
結語
本文在參考前人的基礎之上,介紹了遺傳演算法和TSP問題,並用Python實現了演算法。剛接觸遺傳演算法,實現的效果還有很多可以優化的地方。