A Guide to Disjoint Sets

Maybe you’ve heard about merge-find sets, or union-find forests, or perhaps disjoint sets. Surely such a pedantic name is that of a correspondly complicated data structure… right? ?

Well… not really — conceiving a data structure that can store disjoint sets is not actually all that hard.

What are sets?

Before we take a look at disjoint sets, what exactly are sets? A set is really just a collection of elements.

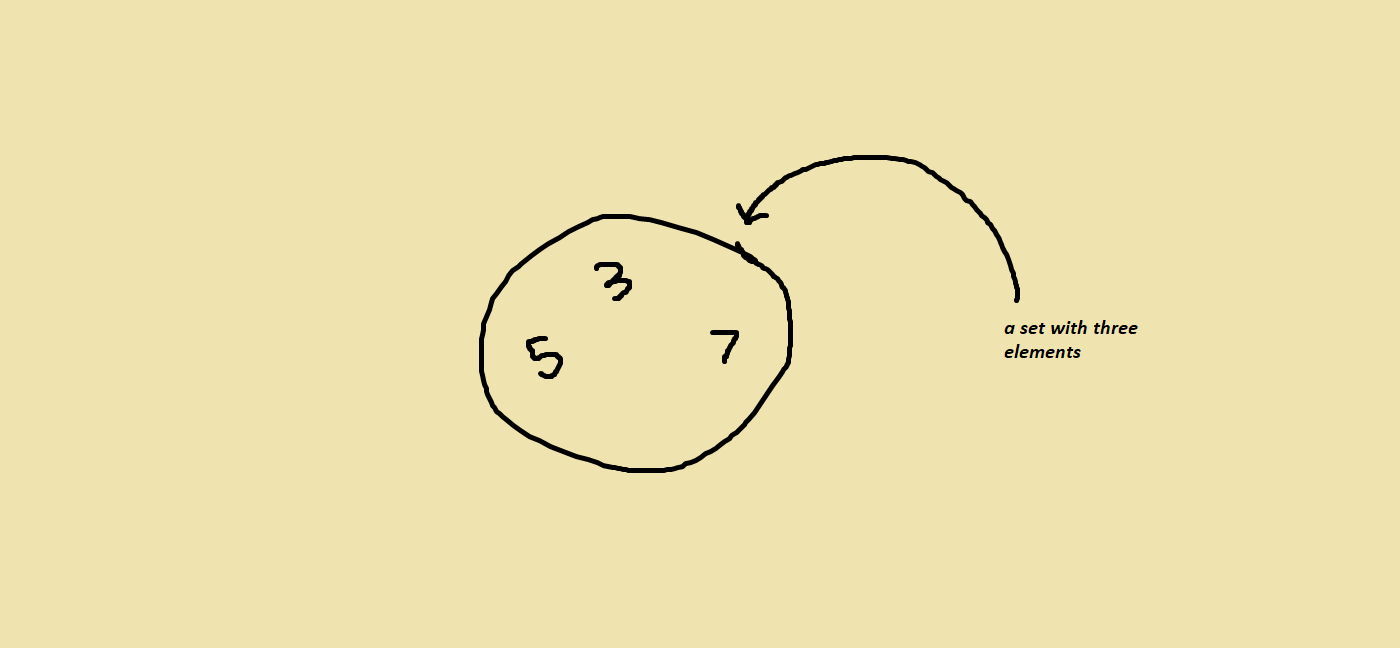
As you can see from the visualization above, sets don’t maintain an order of elements. We can perform pretty much any operation you can perform on a set of data — addition, deletion, size, etc. — except for operations that require an order of the elements to be known.

For example, a few things sets can’t do are inserting at an “index”, popping, or pushing elements, etc.

Another interesting thing about sets — what happens when we add an element to a set that already exists in it?

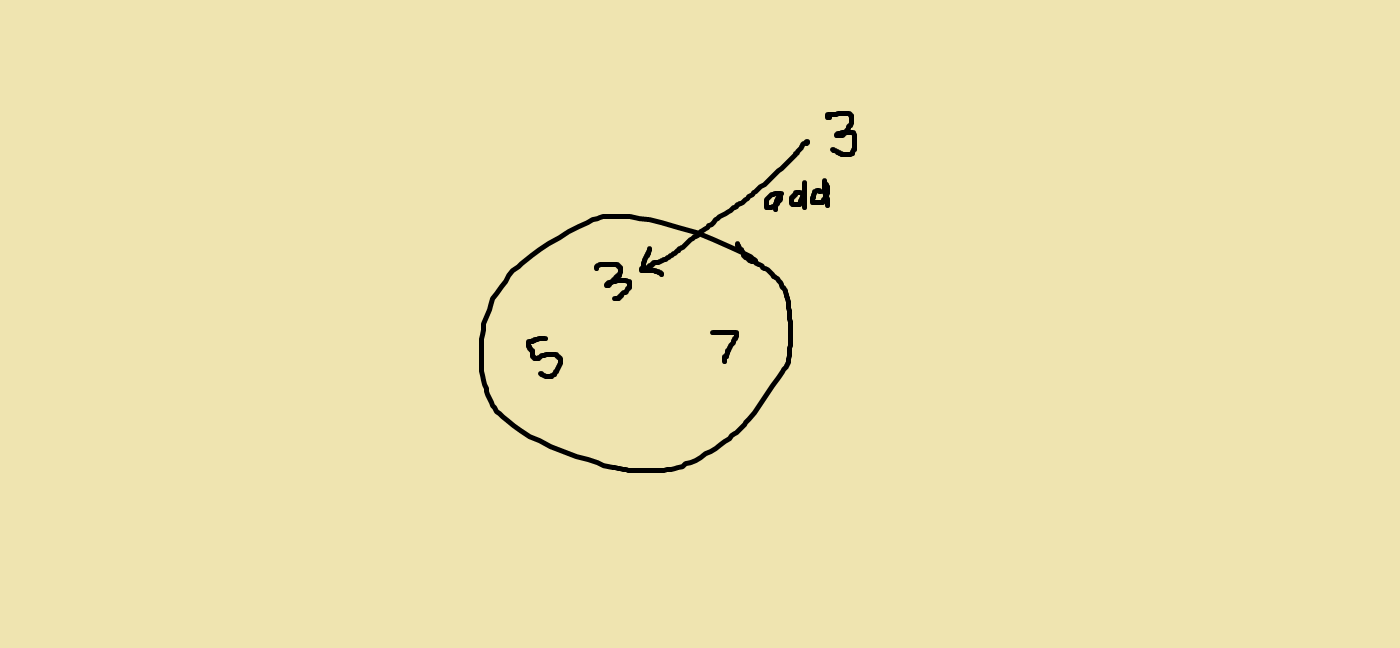
That’s right — we simply replace the element that was already there; we don’t do anything.

There’s a simple reason for why sets don’t store duplicates. In other data structures such as lists and dictionaries, every element was different in at least one way. Even if two entries had the same value, they had to have different indices or keys. But in a set, we’re just storing the elements by themselves in no particular order. So we can’t distinguish a 3 we add in first from a 3 we add in later.

What are disjoint sets?

Now that you know what sets are, a group of disjoint sets is really just a bunch of sets where each set has a representative element.

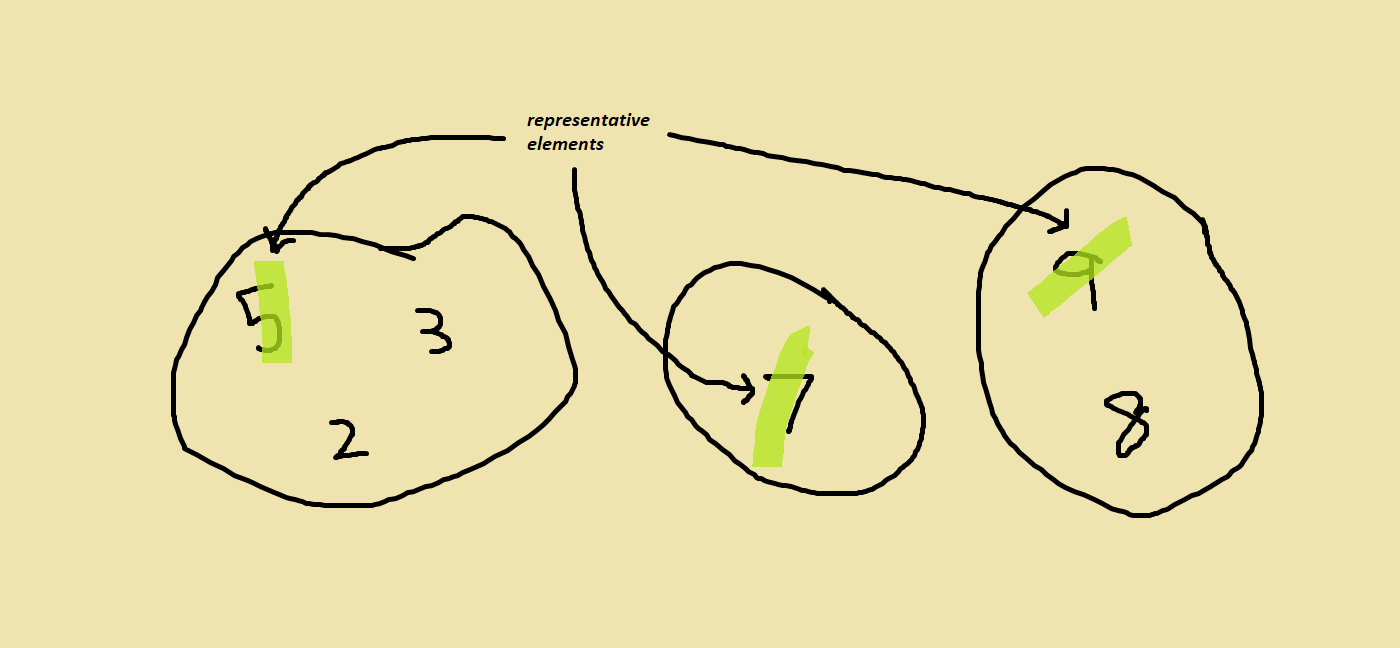
That’s really all a data structure holding disjoint sets needs to keep track of — a bunch of elements and the representative element of the set they belong to.

The operations you can perform on disjoint sets are also quite simple -

• Make a new set with a new representative element
• Find the representative element of the set an element belongs to
• Union the sets two elements belong to

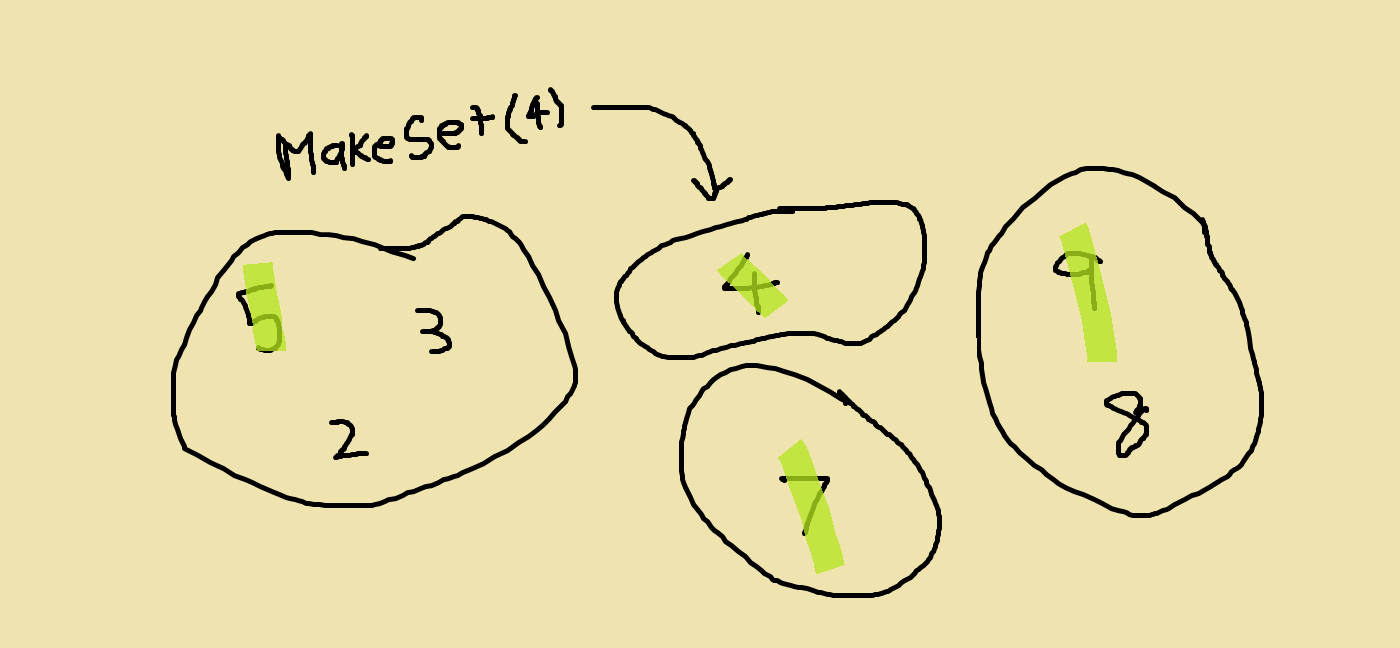
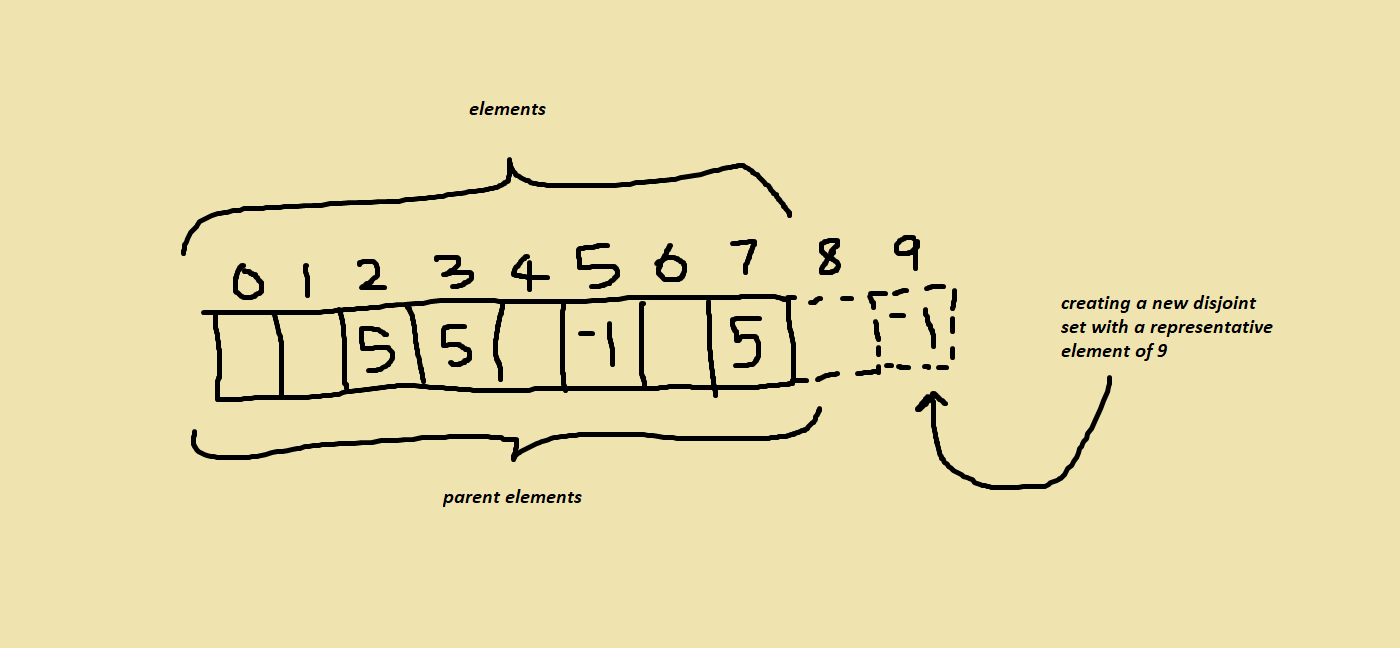
The first operation is making a new disjoint set and putting an element in it. This element will be its representative element. This is shown in the below visualization.

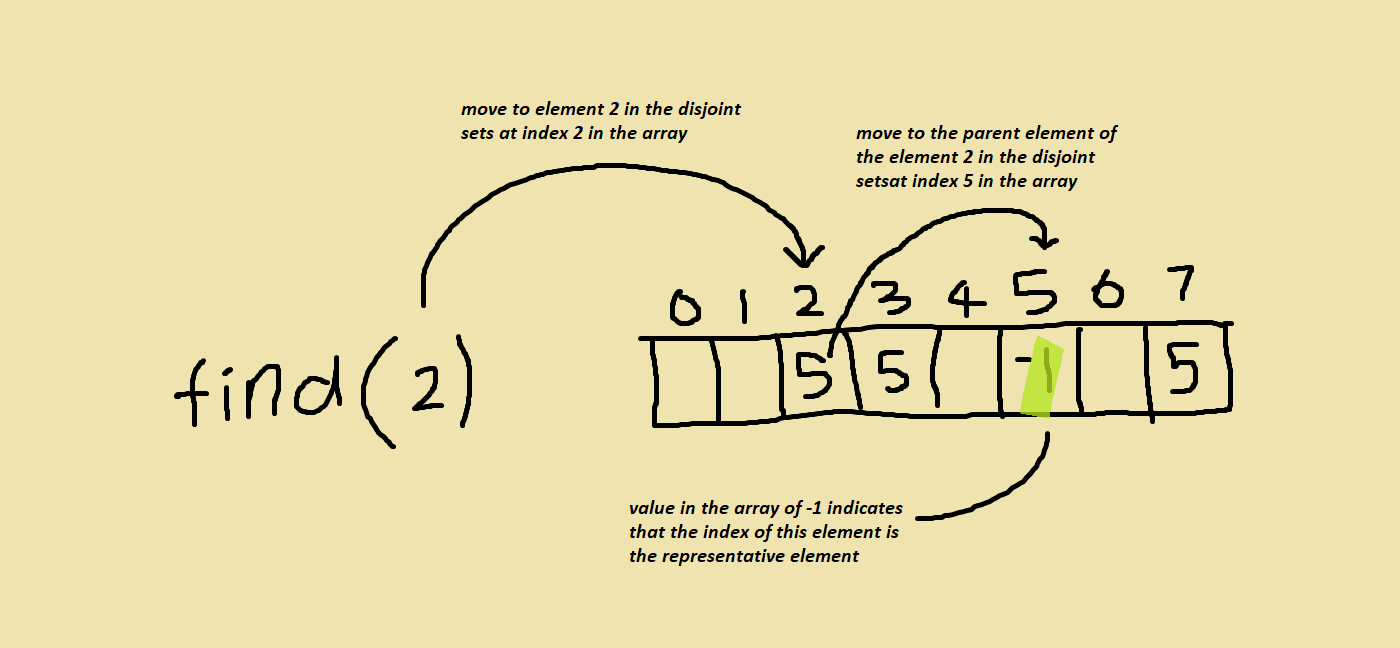
The second operation is finding the representative element of the set an element belongs to. In a previous picture, we saw that the representative element of the set with {5, 3, 2} is 5. So the representative element of 3 is 5 because 3 is in the set which has 5 as its representative element.

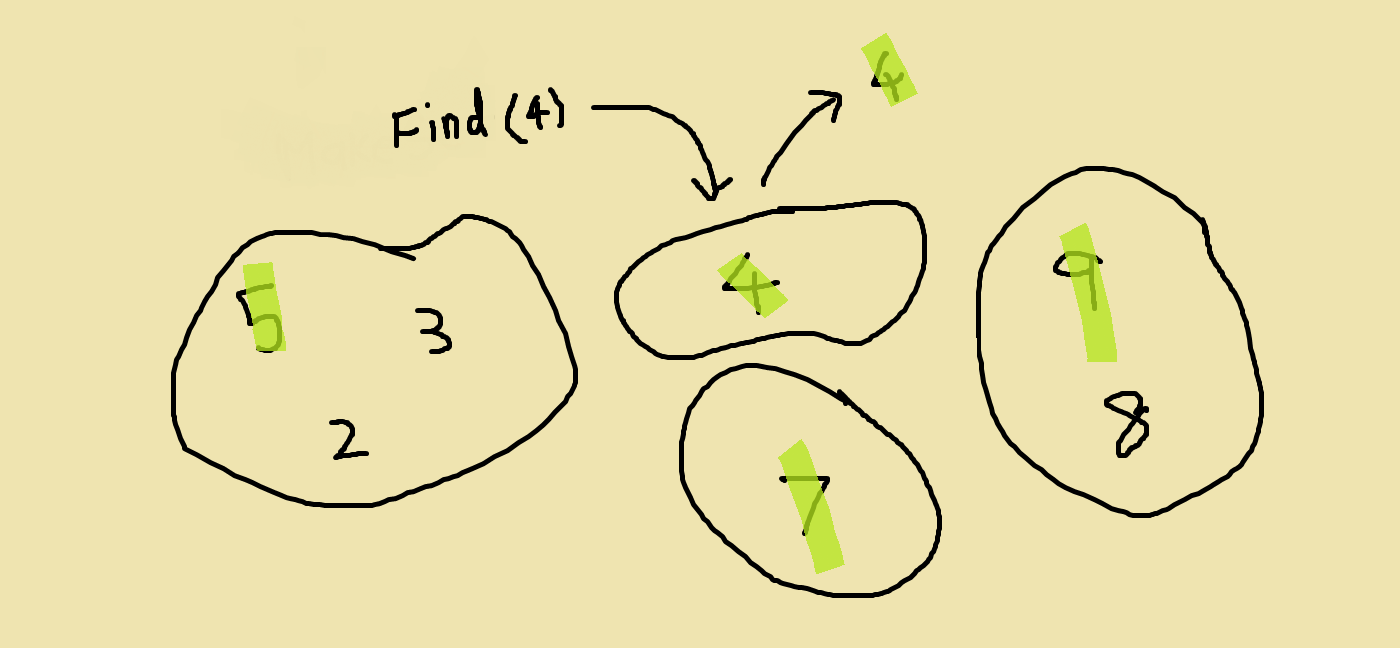
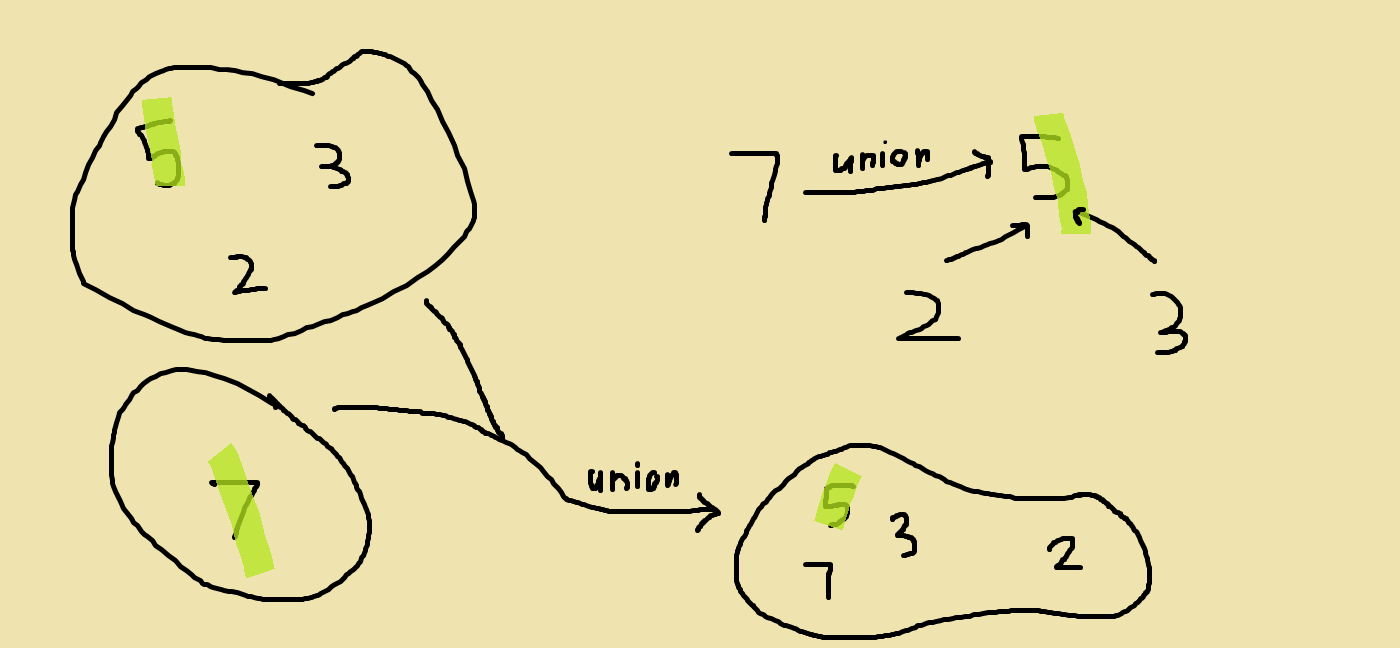
The third operation is taking the union of the sets that contain two elements. So what’s a union? A union of two sets is what we get when we take all the elements of one set and all the elements of the other set and put them together into the same set. Here’s what that looks like.

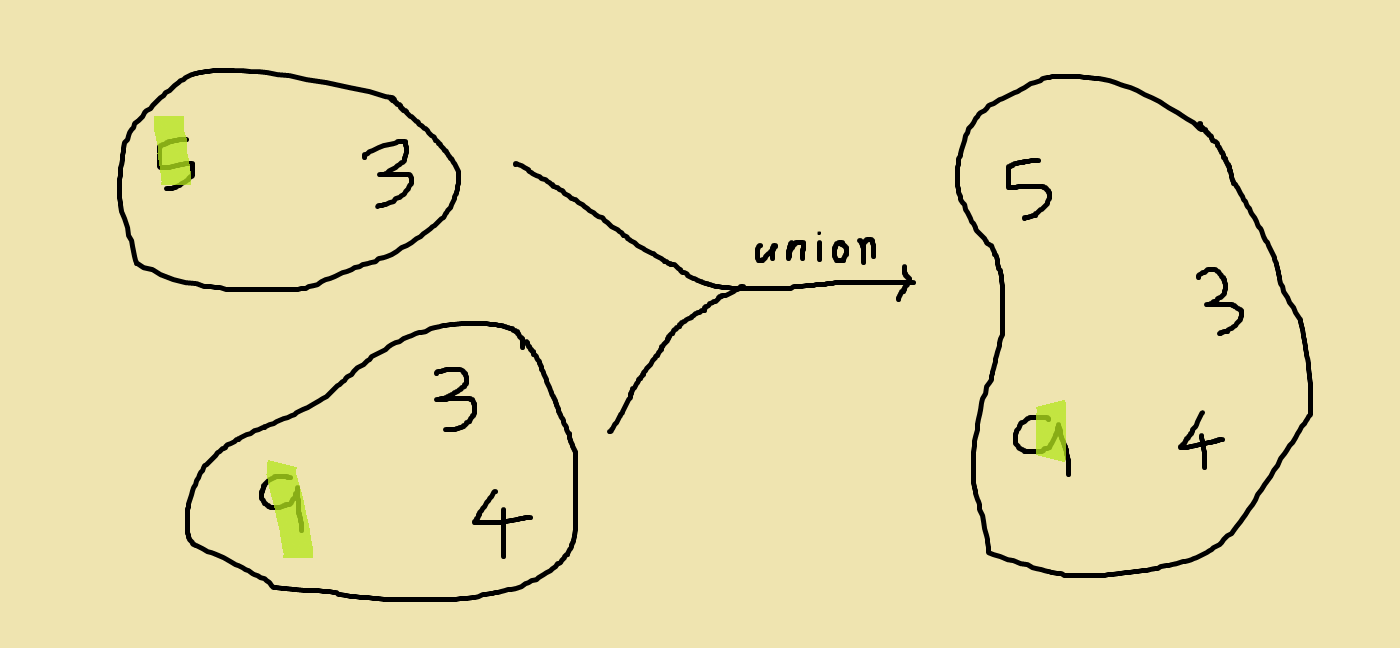
As you can see, we pretty much just took the elements in both sets and put them together in the same set. However there are two other things you should notice.

1. We kept only one 3 even though there was 1 in both sets. This is something we have to do be because, as we mentioned earlier, we can’t distinguish the 3 from the first set from the 3 from the other set. So instead, we just keep one of them.
2. We also had to pick a new representative element for the new set. Naturally, we picked one of two representative elements of the original set. But why did we pick the 9 and not the 5? The answer is that it doesn’t really matter that much which one we pick. Depending on how we implement our disjoint set data structure, we might choose to pick either one.

Now that we’ve seen the two things we need to keep track of for disjoint sets (all the elements, the representative elements of the sets they belong to) and the three operations we need to be able to perform (make a new set, find a representative element, and union two sets). Let’s move on to how we would actually implement these sets.

How to implement disjoint sets

So how exactly do we implement a data structure that stores disjoint sets?

One way we can store disjoint sets is with a tree-like structure. For example we can represent the following disjoint sets as follows.

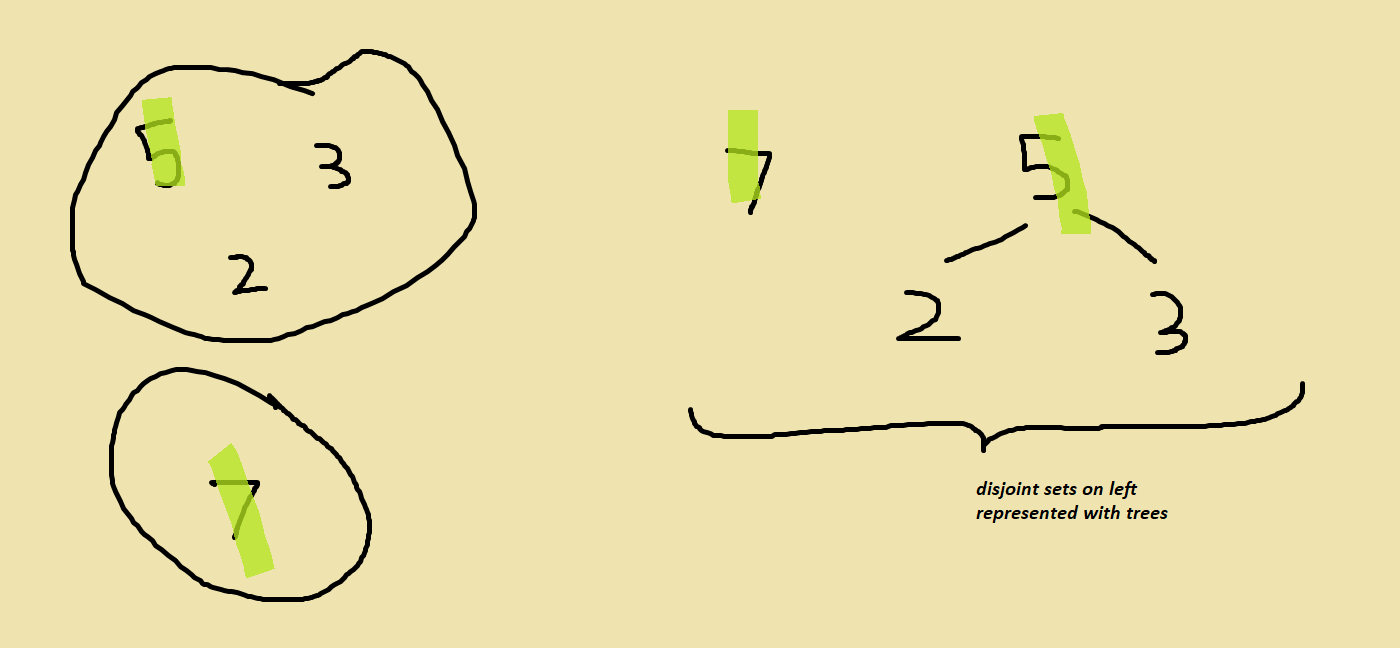
If we use some sort of tree-like structure, all we have to do to make a set is create a new “tree” with the representative element of the new set at the root or the top of the tree. To find the representative element of the set an element belongs to, we simply have to follow the element up the tree till we get to the representative element at the top. To take the union of two sets we simply have to make the root of one set’s tree point to the root of other other set’s tree.

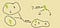
So it looks like trees are a great way of representing disjoint sets. We can store everything we want to and perform the operations we want to. But what do we actually use to store the trees?

As it turns out arrays can be used quite effectively to store these “disjoint set trees”. We can have an array and each element can correspond to an index in our array and the parent of that element in the tree can correspond to the element at that index in our array. Here’s what that would look like.

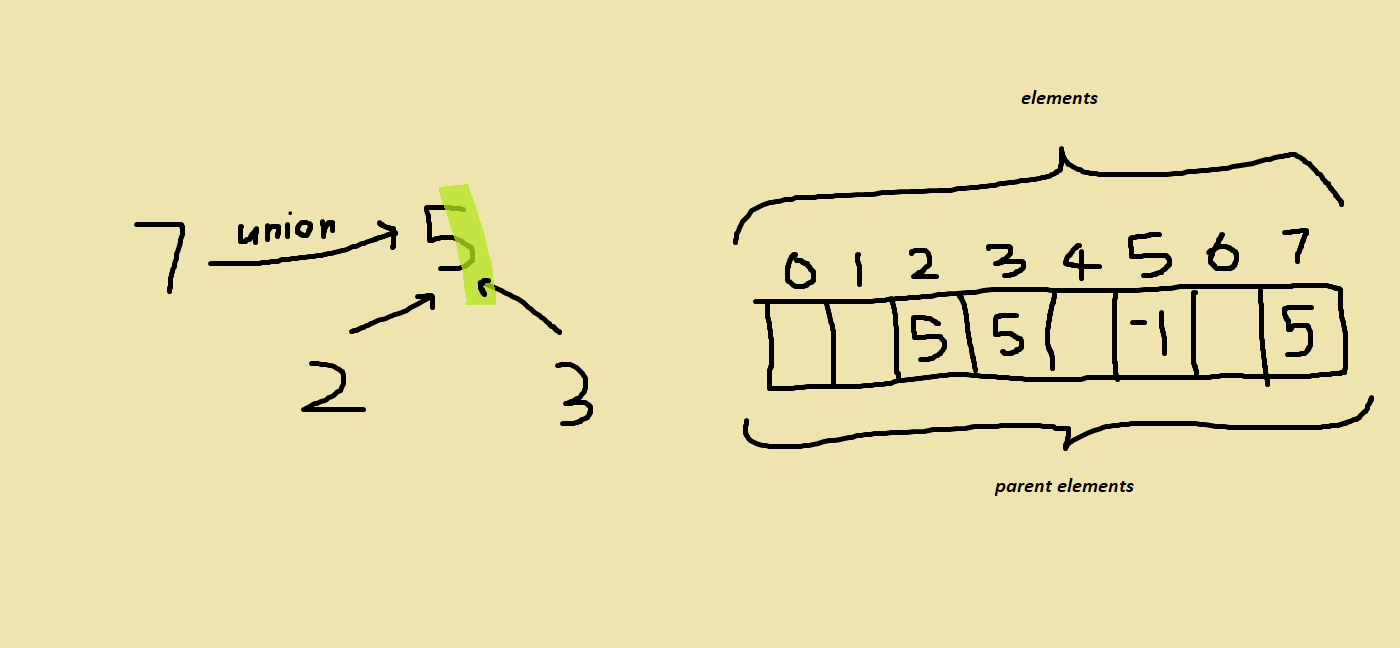
As you can see the elements at indices 2, 3, and 7 represented the parents of elements 2, 3, and 7 in the disjoint set tree. They all had a value of 5 because that’s what their parent element is in the tree.

And you can also notice that the element at index 5 was a -1. When we are trying to find the representative element of a set an element belongs to, we can keep moving to the parent of the current element till we get to one with a value of -1. Then we can know to stop because the current element’s index is the representative element.

So just to summarize — here’s how we can perform our three operations on disjoint sets using an array.

• We can make a new set by simply adding an element to the array at the index of the value we want the set’s representative element to have.

• We can find the representative element of the set an element belongs to by repeatedly moving a pointer to the parent element of the original element.

• Lastly, we can also take the union of two sets by simply setting the parent value of the representative element of one to set to the value of the representative element of the other set.

How to make disjoint sets work for stuff other than number

Up to this point, we’ve just been looking at disjoint sets where all the elements are numbers. However, it is possible for our disjoint set data structure to support any type of data. The simplest solution is to maintain a dictionary that maps data in the type we want to corresponding numbers in our disjoint sets.

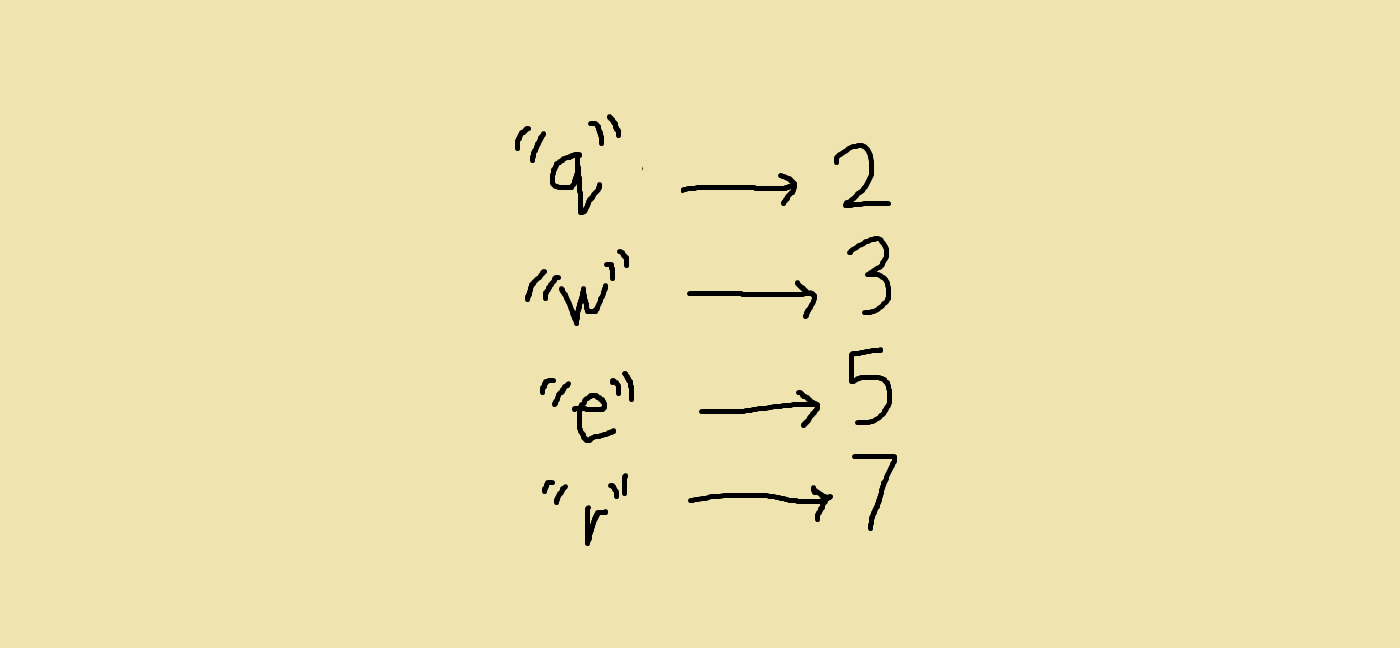
How to optimize our disjoint set data structure

There are actually a few simple optimizations we can do to speed up the operations our disjoint set data structure can do. We’re going to take a look at the two most common ones.

The first is union-by-height. It turns out that even though we can randomly choose which element to choose as the representative element of the union of two sets, by making the element from the set with a taller tree, we can increase performance.

The second is path compression. When we try to find the representative element of an element’s set, the representative element we return in the end is technically the representative element of every element we come across. So, we can modify our find function to simply set the parent of each element we come across to the representative element we ultimately find.