SPFA 最短路演算法 求負環(POJ3259)多圖負環
阿新 • • 發佈:2018-12-29
什麼是 SPFA
Bellman-ford的佇列優化,即SPFA
- 本質思想:每次從佇列中取出一個點,利用這個點出發的所有邊更新所有的終點距離,若更新成功,且被更新的點不在佇列裡,就把它放入佇列。
- 實現:佇列初始只放第一個點,也是用一個dis陣列,然後跑個不停。再用一個布林陣列記錄一個點在不在佇列裡。
- 若一個點入隊了大於N次,則存在負環。
- 一般不會用鄰接矩陣寫……但也可以用
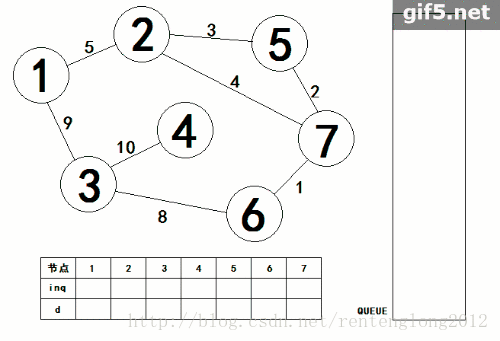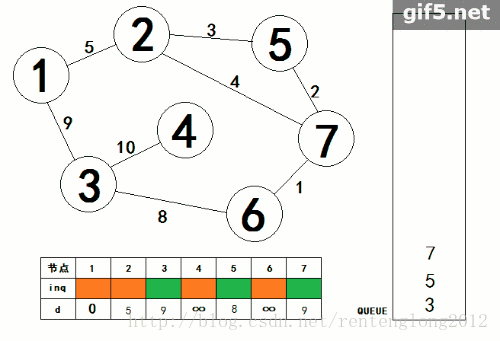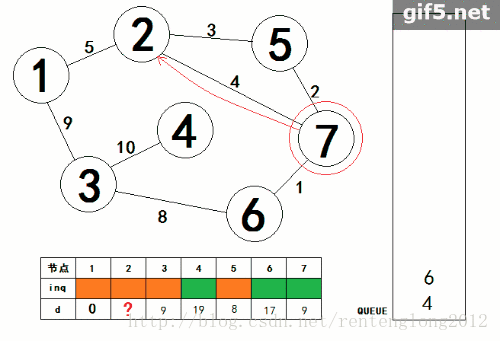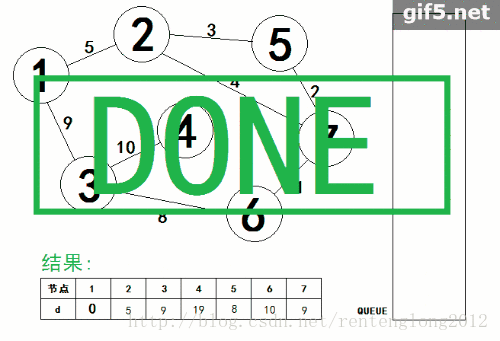
附上大佬部落格連結: SPFA.
然後附上題目連結:Wormholes
題意:有 f 個農場,每個農場有 n 塊地,其間有 m 條路,w條時光隧道,過去的時候時間會倒退 t 秒。判斷是否可以從某塊地出發後又回來,看到了離開之前的自己。
注意:前m條路為雙向邊,時空隧道為單向邊。
方法:Floyd或者SPFA判斷是否存在負權環。
AC程式碼
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#define inf 0x3f3f3f3f
#define N 502
using namespace std;
int n, m, w, Map[N][N];
int dis[N];
bool vis[N];
bool spfa(int x){
///Shortest Path Faster Algorithm 下面說一下我今天一上午做這道題遇到的問題
- 鄰接矩陣大法好,因為要判斷重邊,鄰接表不好判斷重邊
- 出佇列標記vis為未訪問,進棧標記為訪問
- 疏鬆原理更新各個點到終點的距離
- 最最坑的編譯器問題,用了學校的電腦,被設定了某種許可權,使測試結果與樣例結果不符,讓我一直懷疑人生 ,關愛生命,從使用自己電腦開始
補充
- 今天非常細心的紫紫問了我如果整張圖不連通,是不是需要遍歷所有節點做spfa,我一臉懵逼,然後她告訴我神奇的加虛節點操作,加入一個節點聯通所有節點,建立權值為0的虛邊。對當前虛節點進行spfa,若入隊節點大於n+1則存在負環。
#include <iostream>
#include <cstring>
#include <queue>
#include <algorithm>
#define inf 0x3f3f3f3f
#define N 502
using namespace std;
int n, m, w, Map[N][N];
int dis[N];
bool vis[N];
bool spfa(int x){
///Shortest Path Faster Algorithm
vis[x] = true;
dis[x] = 0;
int cnt[N] = {0};
queue<int> q;
q.push(x);
while(!q.empty()){
int t = q.front();
q.pop();
cnt[t]++;
if(cnt[t] > n + 1) return true; // 修改為n+1
vis[t] = false;
for(int i = 1; i <= n; i++){
if(dis[i] > dis[t] + Map[t][i]){
dis[i] = dis[t] + Map[t][i];
if(!vis[i]){
vis[i] = true;
q.push(i);
}
}
}
}
return false;
}
void init(int n){
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
{
Map[i][j] = inf;
}
for(int i = 1; i <= n; i++){
dis[i] = inf;
vis[i] = false;
}
}
int main()
{
int u,v,w_;
int t;
ios::sync_with_stdio(false);
cin >> t;
while(t--){
cin >> n >> m >> w;
init(n);
for(int i = 0; i < m; i++){
cin >> u >> v >> w_;
if(Map[u][v] > w_)
Map[u][v] = Map[v][u] = w_;
}
for(int i = 0; i < w; i++){
cin >> u >>v >> w_;
Map[u][v] = -w_;
}
for(int i = 1; i <= n; i++){ //建立虛節點和虛邊
Map[0][i] = 0;
}
if(spfa(0)) cout << "YES" <<endl;
else cout << "NO" << endl;
}
return 0;
}
