決策樹(一)——基礎演算法
阿新 • • 發佈:2018-12-29
決策樹
定義
根據wikipedia的定義,決策樹學習方法是一種通過決策樹實現從某幾個特徵屬性(分枝)到目標值(葉節點)的預測模型。
一種實現方法是貪心演算法:資料來源按照屬性測試條件分割為子集,然後在生成的每個子集上遞迴執行遞迴分割過程,直到該節點所有子集具有相同的目標變數。
用途:
- 分類/迴歸模型
- 用於特徵選取。基於屬性測試條件(Attribute value tests)最優結果是資料集的強相關特徵的原理。
演算法【ID3/C4.5/CART】
演算法要解決的問題是:選取什麼變數以及用什麼值拆分資料集。
演算法的結束條件:繼續拆分的效果不佳或者超過最大深度,或者子集純度足夠,或者子集的量太少了。-《Machine_Learning_-_A_Probabilistic_Perspective》

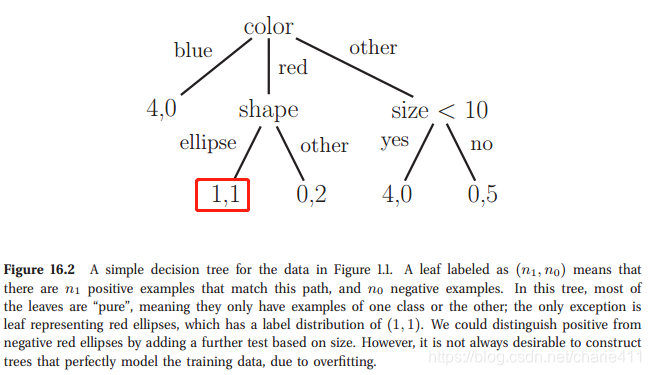
ID3
- 流程
《機器學習實戰》第三章對ID3演算法進行了詳細的介紹,ID3演算法的主要流程是:
-
具體內容
具體地,
1、構造決策樹時,首先需要解決的是當前資料集上哪個變數在拆分資料分類時起決定性作用。為了確定劃分資料集的最佳變數,按照變數標籤迴圈計算拆分前後熵增益,比較得到最大增益對應的變數;
2、完成拆分後,資料子集中某一分支的資料屬於同一型別,則無需進一步對資料集進行拆分,否則需要重複拆分資料子集直至所有相同型別資料均在同一資料子集中。
對應的虛擬碼如下:

-
屬性測試條件的選取:
度量方式是資訊增益 -
演算法不足:
- 切分過於迅速
- 不能直接處理連續型特徵變數
- ID3採用資訊增益大的特徵優先建立決策樹的節點
- ID3演算法沒有考慮缺失值情況
- 沒有考慮過擬合的問題
C4.5
- 針對ID3演算法的改進
- 對於連續型特徵變數,採用排序後的相鄰兩數均值結果作為二拆分節點,利用最佳熵增益比作為判斷指標,將連續的特徵離散化。另:選擇該連續變數作為拆分節點,該屬性後面還可以參與子節點的產生選擇過程。
- 採用資訊增益比改進特徵選取依據
- 對於缺失值處理的問題,主要需要解決的是兩個問題,一是在樣本某些特徵缺失的情況下選擇劃分的屬性,二是選定了劃分屬性,對於在該屬性上缺失特徵的樣本的處理。
- 對於過擬合問題,C4.5引入了正則化係數進行初步的剪枝
- 流程
-
屬性測試條件的選取:
度量方式是資訊增益比 -
演算法不足:
- 必須剪枝
- 多叉樹的執行效率比二叉樹低
- C4.5只能用於分類,不能處理迴歸問題
- C4.5針對連續值選取特徵變數時需要排序和大量對數運算(熵模型),模型較複雜
CART
- 針對C4.5演算法的改進
- 二分離形成二叉樹
- 針對迴歸問題,採用總方差代替熵模型,處理連續值的離散化;另外輸出值是最終葉子的均值或中位數(迴歸樹)、線性模型係數(模型樹)
- 為了降低運算複雜度,採用基尼不純度代替熵模型。
- 流程
- 關於剪枝
- 從原始決策樹生成各種剪枝效果的決策樹;
- 交叉驗證各種剪枝的泛化預測能力,度量剪枝前後損失的指標根據模型種類確定:針對迴歸樹,採用總方差作為評價指標,針對分類樹,採用基尼不純度作為評價指標。
-
屬性測試條件的選取:
《機器學習實戰》中迴歸樹/模型樹的度量方式是總方差
《統計學習方法》中的度量方式是基尼不純度 -
演算法不足:
- 樣本的一點點改動會導致樹結構的劇烈改變—>整合學習解決
- 準確度較低
CHAID
待學習
決策樹演算法小結
- 首先我們看看決策樹演算法的優點:
1)簡單直觀,生成的決策樹很直觀。
2)基本不需要預處理,不需要提前歸一化,處理缺失值。
3)使用決策樹預測的代價是O(log2m)。 m為樣本數。
4)既可以處理離散值也可以處理連續值。很多演算法只是專注於離散值或者連續值。
5)可以處理多維度輸出的分類問題。
6)相比於神經網路之類的黑盒分類模型,決策樹在邏輯上可以得到很好的解釋
7)可以交叉驗證的剪枝來選擇模型,從而提高泛化能力。
8) 對於異常點的容錯能力好,健壯性高。- 我們再看看決策樹演算法的缺點:
1)決策樹演算法非常容易過擬合,導致泛化能力不強。可以通過設定節點最少樣本數量和限制決策樹深度來改進。
2)決策樹會因為樣本發生一點點的改動,就會導致樹結構的劇烈改變。這個可以通過整合學習之類的方法解決。
3)尋找最優的決策樹是一個NP難的問題,我們一般是通過啟發式方法,容易陷入區域性最優。可以通過整合學習之類的方法來改善。
4)有些比較複雜的關係,決策樹很難學習,比如異或。這個就沒有辦法了,一般這種關係可以換神經網路分類方法來解決。
5)如果某些特徵的樣本比例過大,生成決策樹容易偏向於這些特徵。這個可以通過調節樣本權重來改善。
