排序演算法總結(動態圖非常直觀)
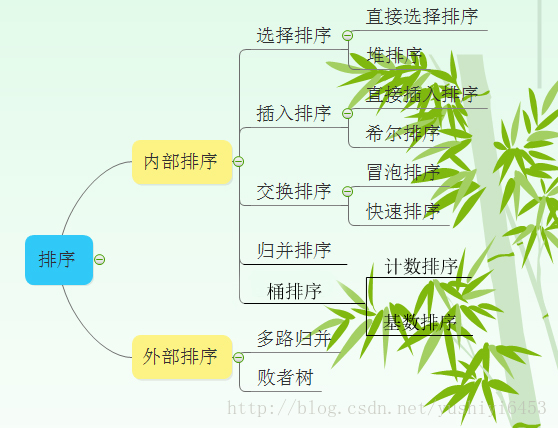
排序演算法分類
排序演算法比較表格填空
| 排序演算法 | 平均時間複雜度 | 最壞時間複雜度 | 空間複雜度 | 是否穩定 |
|---|---|---|---|---|
| 氣泡排序 | :————-: | :—–: | :—–: | :—–: |
| 選擇排序 | :————-: | :—–: | :—–: | :—–: |
| 直接插入排序 | :————-: | :—–: | :—–: | :—–: |
| 歸併排序 | :————-: | :—–: | :—–: | :—–: |
| 快速排序 | :————-: | :—–: | :—–: | :—–: |
| 堆排序 | :————-: | :—–: | :—–: | :—–: |
| 希爾排序 | :————-: | :—–: | :—–: | :—–: |
| 計數排序 | :————-: | :—–: | :—–: | :—–: |
| 基數排序 | :————-: | :—–: | :—–: | :—–: |
排序演算法比較表格
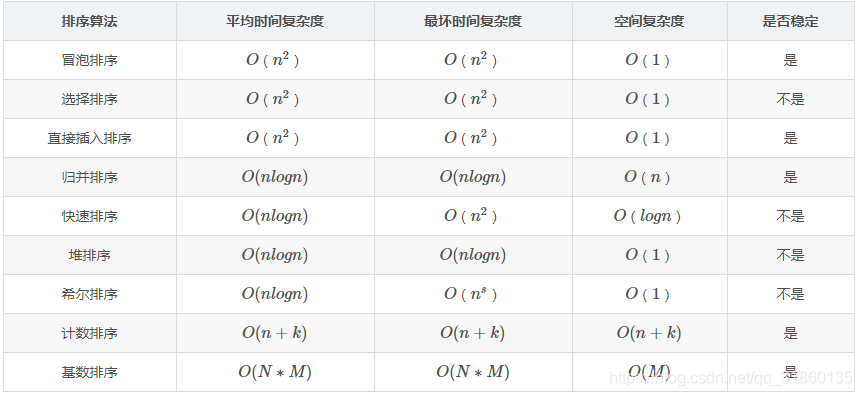
注:
1 歸併排序可以通過手搖演算法將空間複雜度降到O(1),但是時間複雜度會提高。
2 基數排序時間複雜度為O(N*M),其中N為資料個數,M為資料位數。
輔助記憶
- 時間複雜度記憶-
- 冒泡、選擇、直接 排序需要兩個for迴圈,每次只關注一個元素,平均時間複雜度為O(n2)O(n2))
- 穩定性記憶-“快希選堆”(快犧牲穩定性)
- 排序演算法的穩定性:排序前後相同元素的相對位置不變,則稱排序演算法是穩定的;否則排序演算法是不穩定的。
原理理解
1 氣泡排序
1.1 過程
氣泡排序從小到大排序:一開始交換的區間為0~N-1,將第1個數和第2個數進行比較,前面大於後面,交換兩個數,否則不交換。再比較第2個數和第三個數,前面大於後面,交換兩個數否則不交換。依次進行,最大的數會放在陣列最後的位置。然後將範圍變為0~N-2,陣列第二大的數會放在陣列倒數第二的位置。依次進行整個交換過程,最後範圍只剩一個數時陣列即為有序。
1.2 動圖
1.3 核心程式碼(函式)
//array[]為待排序陣列,n為陣列長度
void BubbleSort(int array[], int n)
{
int i, j, k;
for(i=0; i<n-1; i++)
for(j=0; j<n-1-i; j++)
{
if(array[j]>array[j+1])
{
k=array[j];
array[j]=array[j+1];
array[j+1]=k;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
2 選擇排序
2.1 過程
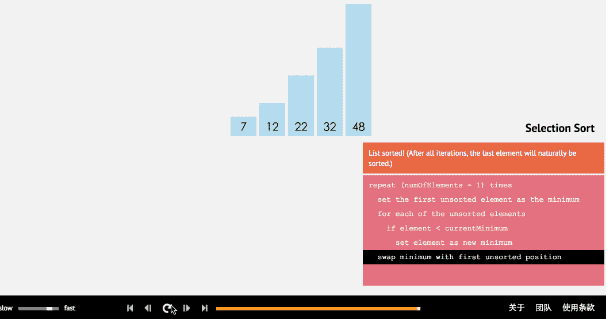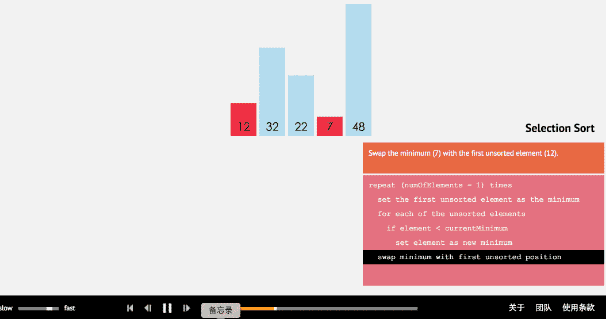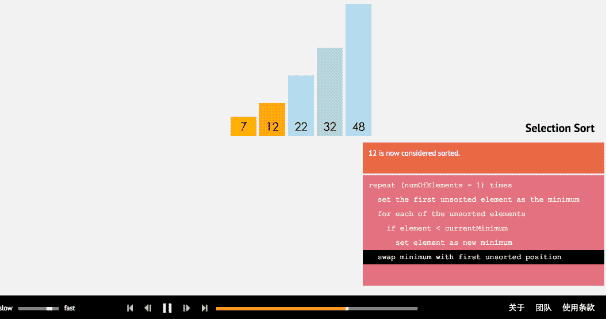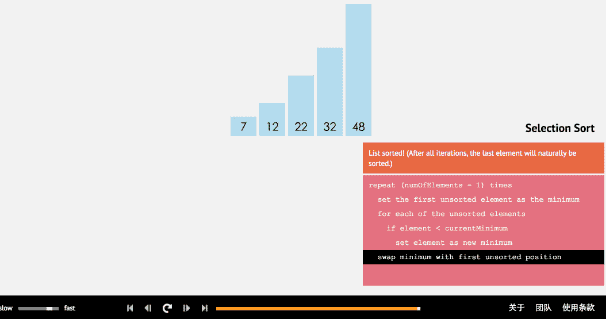
選擇排序從小到大排序:一開始從0~n-1區間上選擇一個最小值,將其放在位置0上,然後在1~n-1範圍上選取最小值放在位置1上。重複過程直到剩下最後一個元素,陣列即為有序。
2.2 動圖

2.3 核心程式碼(函式)
//array[]為待排序陣列,n為陣列長度
void selectSort(int array[], int n)
{
int i, j ,min ,k;
for( i=0; i<n-1; i++)
{
min=i; //每趟排序最小值先等於第一個數,遍歷剩下的數
for( j=i+1; j<n; j++) //從i下一個數開始檢查
{
if(array[min]>array[j])
{
min=j;
}
}
if(min!=i)
{
k=array[min];
array[min]=array[i];
array[i]=k;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
3 插入排序
3.1 過程
插入排序從小到大排序:首先位置1上的數和位置0上的數進行比較,如果位置1上的數大於位置0上的數,將位置0上的數向後移一位,將1插入到0位置,否則不處理。位置k上的數和之前的數依次進行比較,如果位置K上的數更大,將之前的數向後移位,最後將位置k上的數插入不滿足條件點,反之不處理。
3.2 動圖
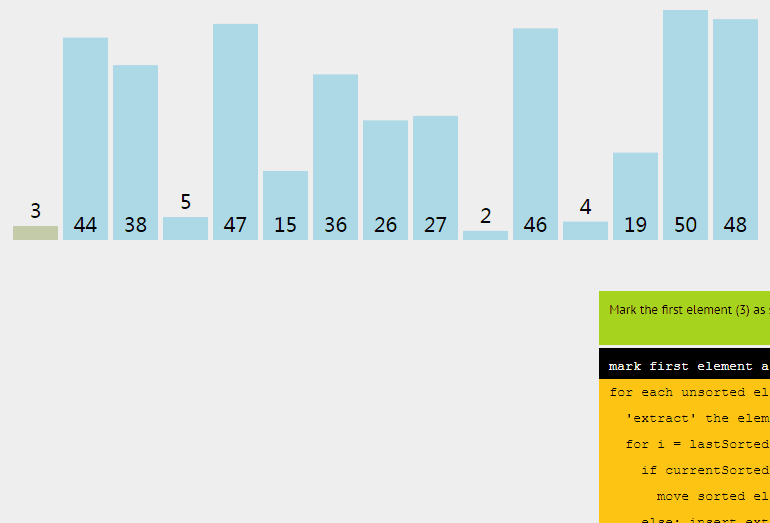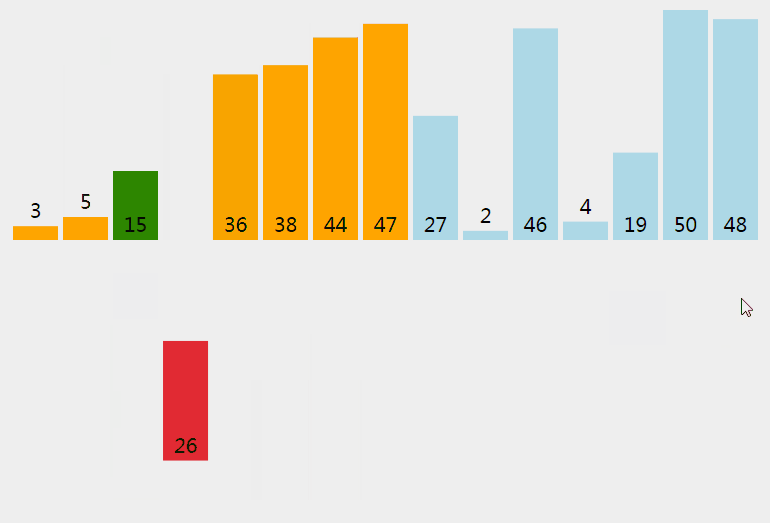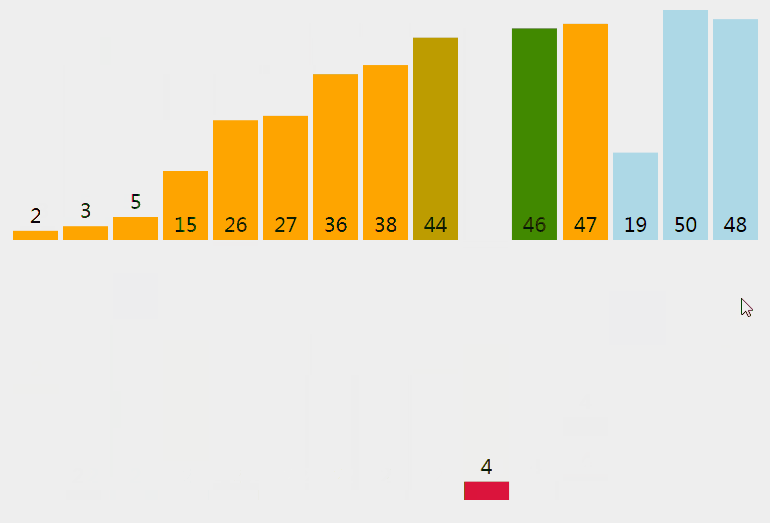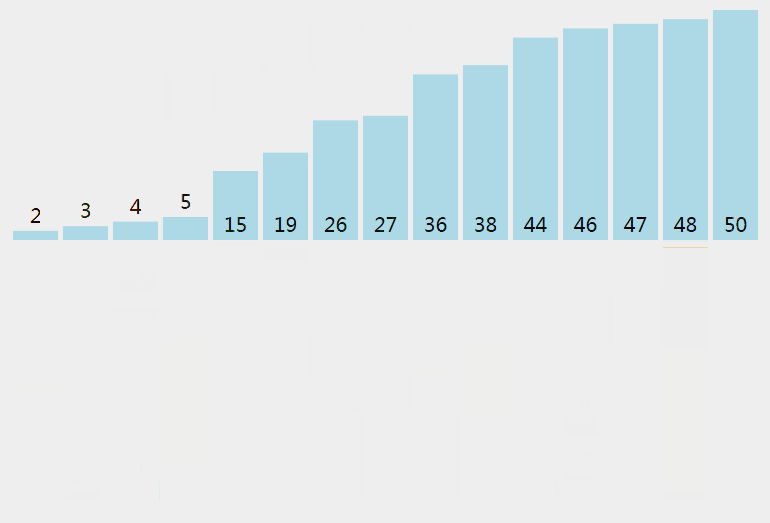
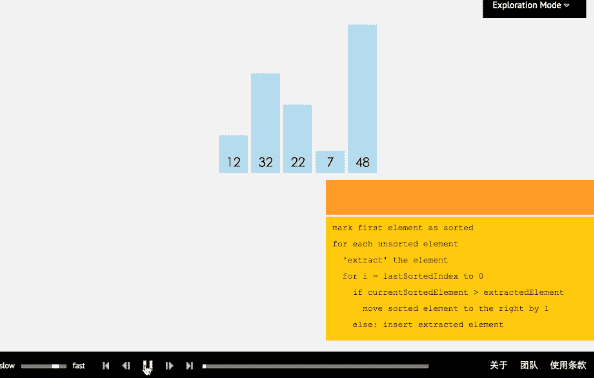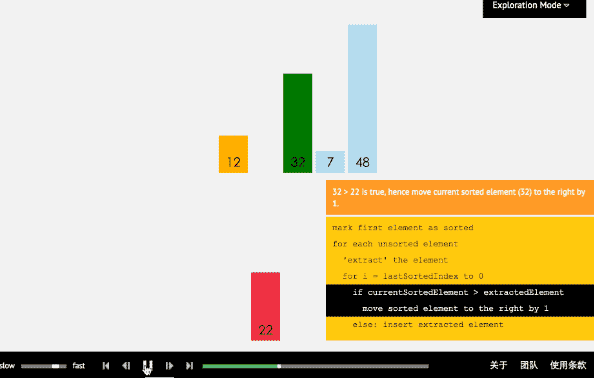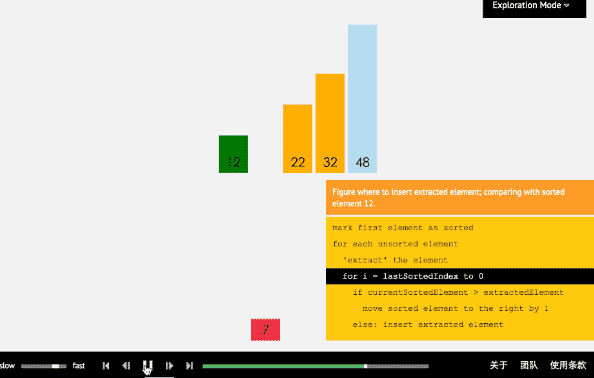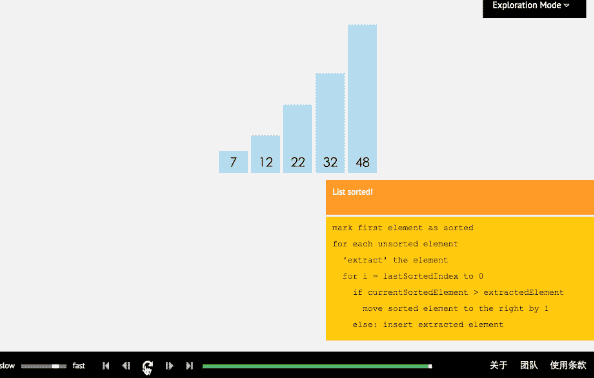
3.3 核心程式碼(函式)
//array[]為待排序陣列,n為陣列長度
void insertSort(int array[], int n)
{
int i,j,temp;
for( i=1;i<n;i++)
{
if(array[i]<array[i-1])
{
temp=array[i];
for( j=i;array[j-1]>temp;j--)
{
array[j]=array[j-1];
}
array[j]=temp;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
4 歸併排序
4.1 過程
歸併排序從小到大排序:首先讓陣列中的每一個數單獨成為長度為1的區間,然後兩兩一組有序合併,得到長度為2的有序區間,依次進行,直到合成整個區間。
4.2 動圖
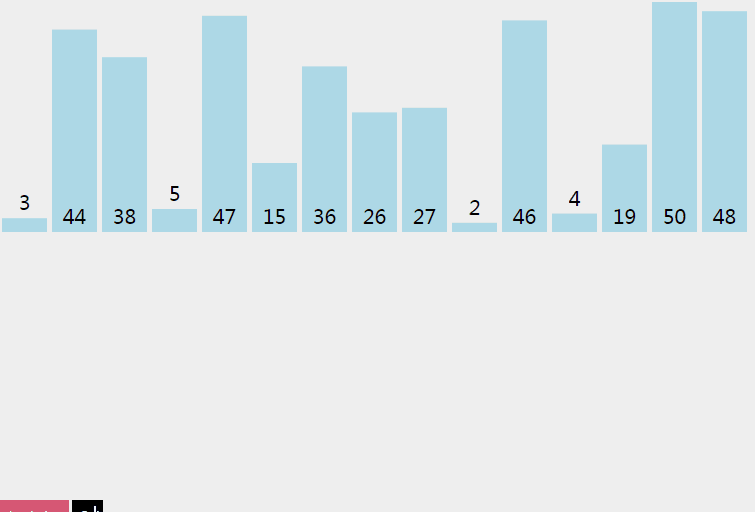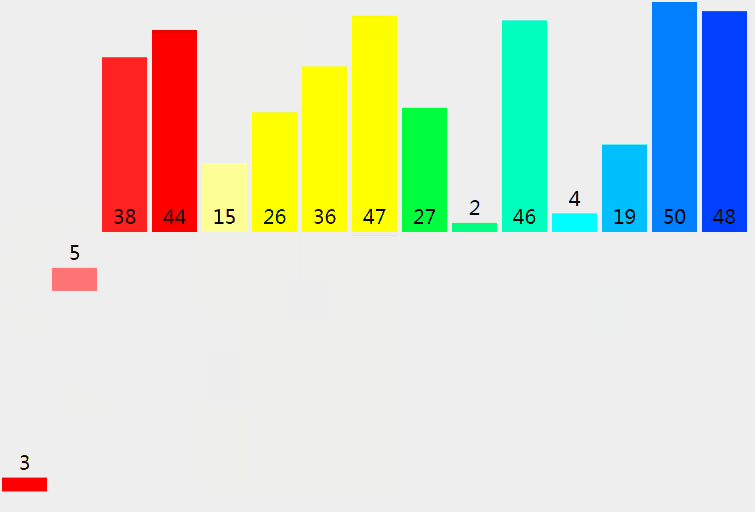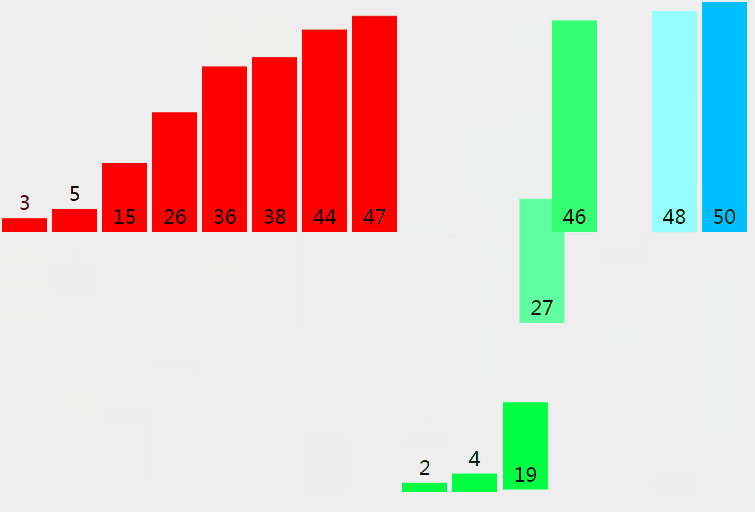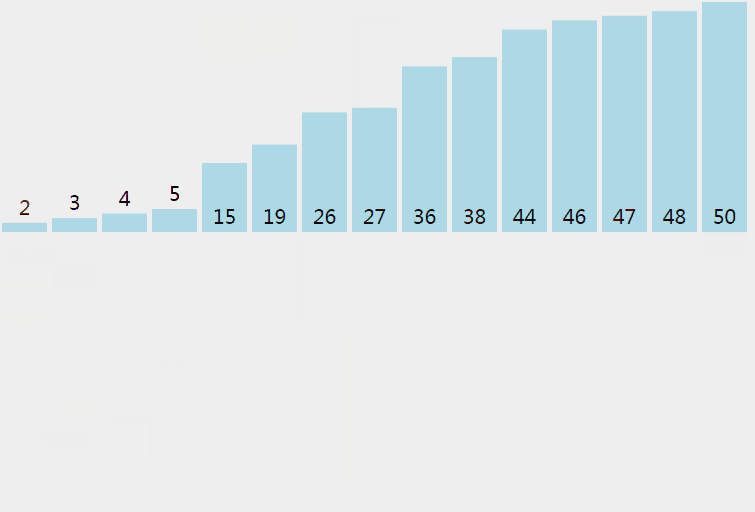

4.3 核心程式碼(函式)
- 遞迴實現
////實現歸併,並把資料都放在list1裡面
void merging(int *list1, int list1_size, int *list2, int list2_size)
{
int i=0, j=0, k=0, m=0;
int temp[MAXSIZE];
while(i < list1_size && j < list2_size)
{
if(list1[i]<list2[j])
{
temp[k++] = list1[i++];
}
else
{
temp[k++] = list2[j++];
}
}
while(i<list1_size)
{
temp[k++] = list1[i++];
}
while(j<list2_size)
{
temp[k++] = list2[j++];
}
for(m=0; m < (list1_size+list2_size); m++)
{
list1[m]=temp[m];
}
}
//如果有剩下的,那麼說明就是它是比前面的陣列都大的,直接加入就可以了
void mergeSort(int array[], int n)
{
if(n>1)
{
int *list1 = array;
int list1_size = n/2;
int *list2 = array + n/2;
int list2_size = n-list1_size;
mergeSort(list1, list1_size);
mergeSort(list2, list2_size);
merging(list1, list1_size, list2, list2_size);
}
}
//歸併排序複雜度分析:一趟歸併需要將待排序列中的所有記錄
//掃描一遍,因此耗費時間為O(n),而由完全二叉樹的深度可知,
//整個歸併排序需要進行[log2n],因此,總的時間複雜度為
//O(nlogn),而且這是歸併排序演算法中平均的時間效能
//空間複雜度:由於歸併過程中需要與原始記錄序列同樣數量級的
//儲存空間去存放歸併結果及遞迴深度為log2N的棧空間,因此空間
//複雜度為O(n+logN)
//也就是說,歸併排序是一種比較佔記憶體,但卻效率高且穩定的演算法
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 迭代實現
void MergeSort(int k[],int n)
{
int i,next,left_min,left_max,right_min,right_max;
//動態申請一個與原來陣列一樣大小的空間用來儲存
int *temp = (int *)malloc(n * sizeof(int));
//逐級上升,第一次比較2個,第二次比較4個,第三次比較8個。。。
for(i=1; i<n; i*=2)
{
//每次都從0開始,陣列的頭元素開始
for(left_min=0; left_min<n-i; left_min = right_max)
{
right_min = left_max = left_min + i;
right_max = left_max + i;
//右邊的下標最大值只能為n
if(right_max>n)
{
right_max = n;
}
//next是用來標誌temp陣列下標的,由於每次資料都有返回到K,
//故每次開始得重新置零
next = 0;
//如果左邊的資料還沒達到分割線且右邊的陣列沒到達分割線,開始迴圈
while(left_min<left_max&&right_min<right_max)
{
if(k[left_min] < k[right_min])
{
temp[next++] = k[left_min++];
}
else
{
temp[next++] = k[right_min++];
}
}
//上面迴圈結束的條件有兩個,如果是左邊的遊標尚未到達,那麼需要把
//陣列接回去,可能會有疑問,那如果右邊的沒到達呢,其實模擬一下就可以
//知道,如果右邊沒到達,那麼說明右邊的資料比較大,這時也就不用移動位置了
while(left_min < left_max)
{
//如果left_min小於left_max,說明現在左邊的資料比較大
//直接把它們接到陣列的min之前就行
k[--right_min] = k[--left_max];
}
while(next>0)
{
//把排好序的那部分陣列返回該k
k[--right_min] = temp[--next];
}
}
}
}
//非遞迴的方法,避免了遞迴時深度為log2N的棧空間,
//空間只是用到歸併臨時申請的跟原來陣列一樣大小的空間,並且在時間效能上也有一定的提升,
//因此,使用歸併排序是,儘量考慮用非遞迴的方法。
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
5 快速排序
5.1 過程
快速排序從小到大排序:在陣列中隨機選一個數(預設陣列首個元素),陣列中小於等於此數的放在左邊,大於此數的放在右邊,再對陣列兩邊遞迴呼叫快速排序,重複這個過程。
5.2 動圖
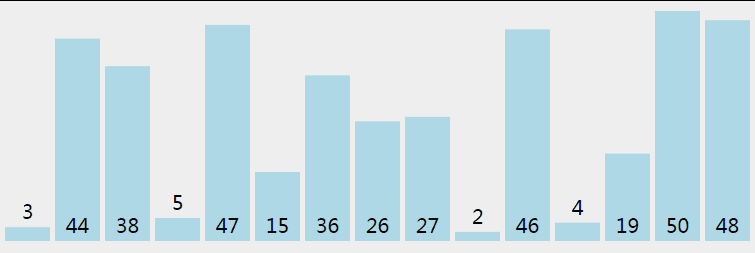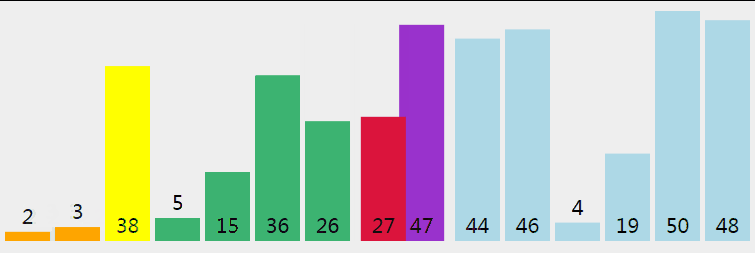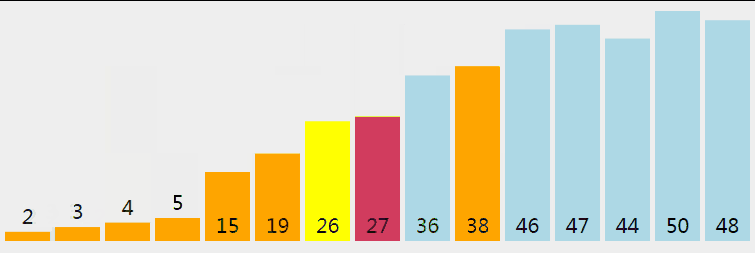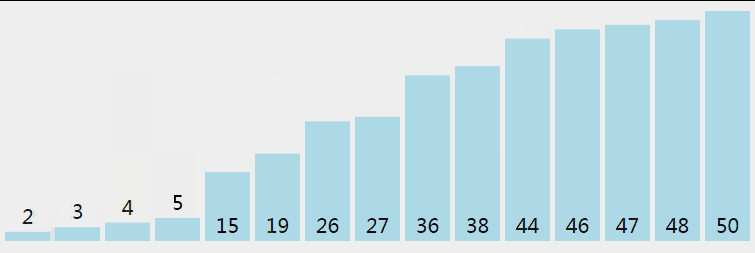

5.3 核心程式碼(函式)
推薦程式(好理解)
//介面調整
void adjust_quicksort(int k[],int n)
{
quicksort(k,0,n-1);
}
void quicksort(int a[], int left, int right)
{
int i,j,t,temp;
if(left>right) //(遞迴過程先寫結束條件)
return;
temp=a[left]; //temp中存的就是基準數
i=left;
j=right;
while(i!=j)
{
//順序很重要,要先從右邊開始找(最後交換基準時換過去的數要保證比基準小,因為基準
//選取陣列第一個數,在小數堆中)
while(a[j]>=temp && i<j)
j--;
//再找右邊的
while(a[i]<=temp && i<j)
i++;
//交換兩個數在陣列中的位置
if(i<j)
{
t=a[i];
a[i]=a[j];
a[j]=t;
}
}
//最終將基準數歸位 (之前已經temp=a[left]過了,交換隻需要再進行兩步)
a[left]=a[i];
a[i]=temp;
quicksort(left,i-1);//繼續處理左邊的,這裡是一個遞迴的過程
quicksort(i+1,right);//繼續處理右邊的 ,這裡是一個遞迴的過程
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
6 堆排序
6.1 過程
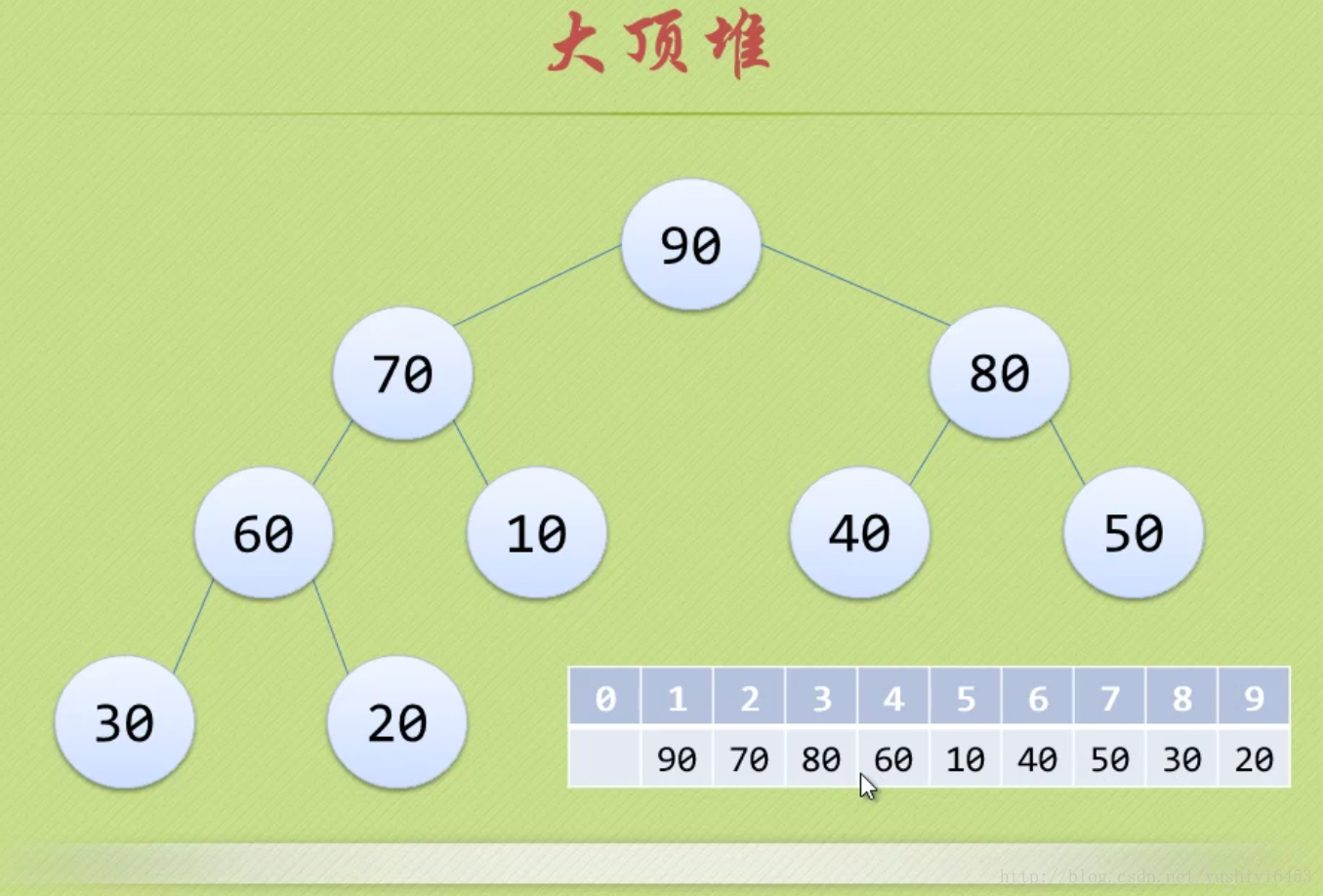
堆排序從小到大排序:首先將陣列元素建成大小為n的大頂堆,堆頂(陣列第一個元素)是所有元素中的最大值,將堆頂元素和陣列最後一個元素進行交換,再將除了最後一個數的n-1個元素建立成大頂堆,再將最大元素和陣列倒數第二個元素進行交換,重複直至堆大小減為1。
注:完全二叉樹
假設二叉樹深度為n,除了第n層外,n-1層節點都有兩個孩子,第n層節點連續從左到右。如下圖
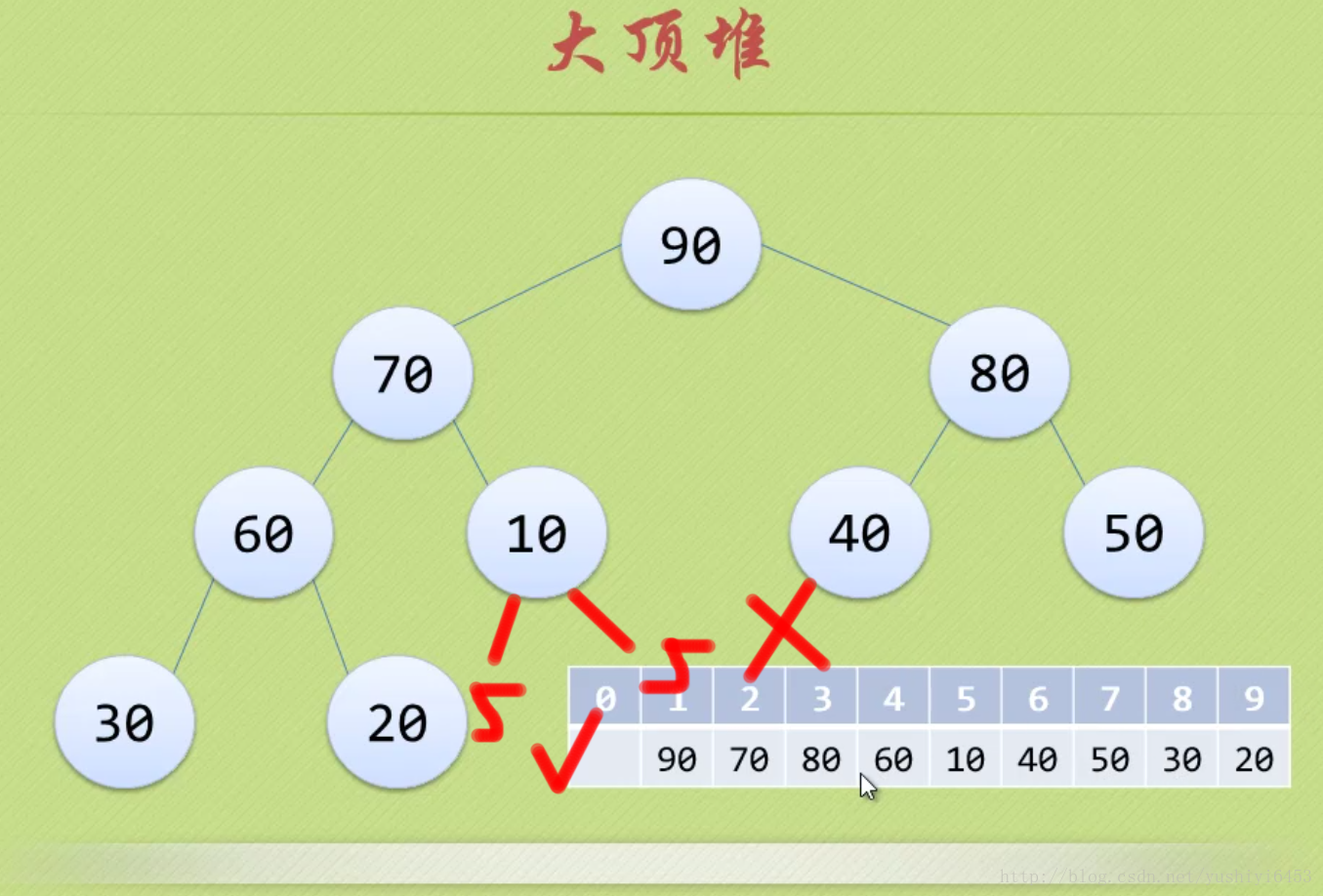
注:大頂堆
大頂堆是具有以下性質的完全二叉樹:每個節點的值都大於或等於其左右孩子節點的值。
即,根節點是堆中最大的值,按照層序遍歷給節點從1開始編號,則節點之間滿足如下關係:
(1<=i<=n/2)
6.2 動圖
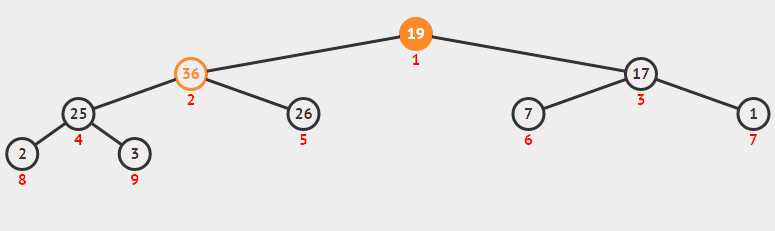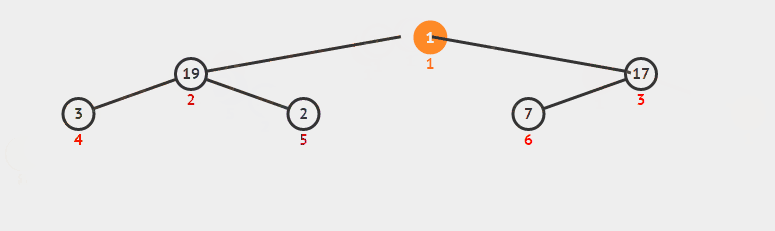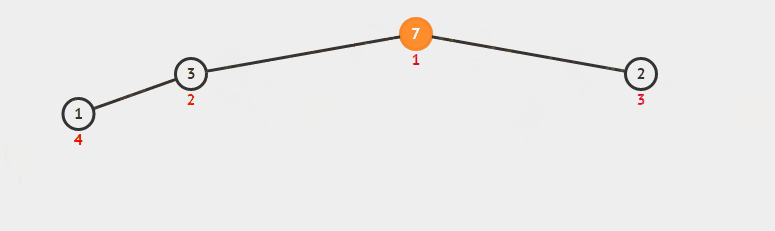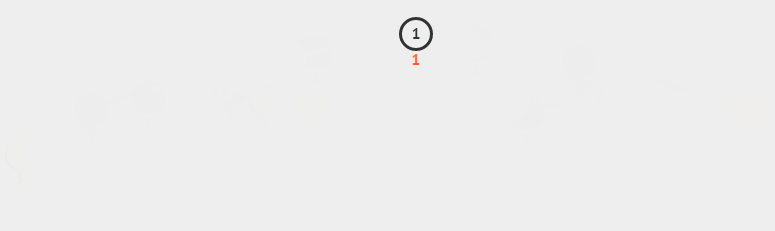

6.3 核心程式碼(函式)
注意!!!陣列從1開始,1~n
void heapSort(int array[], int n)
{
int i;
for (i=n/2;i>0;i--)
{
HeapAdjust(array,i,n);//從下向上,從右向左調整
}
for( i=n;i>1;i--)
{
swap(array, 1, i);
HeapAdjust(array, 1, i-1);//從上到下,從左向右調整
}
}
void HeapAdjust(int array[], int s, int n )
{
int i,temp;
temp = array[s];
for(i=2*s;i<=n;i*=2)
{
if(i<n&&array[i]<array[i+1])
{
i++;
}
if(temp>=array[i])
{
break;
}
array[s]=array[i];
s=i;
}
array[s]=temp;
}
void swap(int array[], int i, int j)
{
int temp;
temp=array[i];
array[i]=array[j];
array[j]=temp;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
7 希爾排序
7.1 過程
希爾排序是插入排序改良的演算法,希爾排序步長從大到小調整,第一次迴圈後面元素逐個和前面元素按間隔步長進行比較並交換,直至步長為1,步長選擇是關鍵。
7.2 動圖

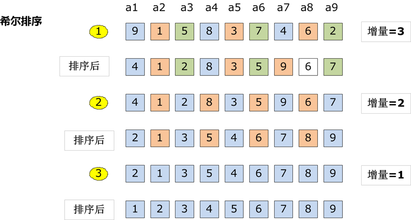
7.3 核心程式(函式)
//下面是插入排序
void InsertSort( int array[], int n)
{
int i,j,temp;
for( i=0;i<n;i++ )
{
if(array[i]<array[i-1])
{
temp=array[i];
for( j=i-1;array[j]>temp;j--)
{
array[j+1]=array[j];
}
array[j+1]=temp;
}
}
}
//在插入排序基礎上修改得到希爾排序
void SheelSort( int array[], int n)
{
int i,j,temp;
int gap=n; //~~~~~~~~~~~~~~~~~~~~~
do{
gap=gap/3+1; //~~~~~~~~~~~~~~~~~~
for( i=gap;i<n;i++ )
{
if(array[i]<array[i-gap])
{
temp=array[i];
for( j=i-gap;array[j]>temp;j-=gap)
{
array[j+gap]=array[j];
}
array[j+gap]=temp;
}
}
}while(gap>1); //~~~~~~~~~~~~~~~~~~~~~~
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
8 桶排序(基數排序和基數排序的思想)
8.1 過程
桶排序是計數排序的變種,把計數排序中相鄰的m個”小桶”放到一個”大桶”中,在分完桶後,對每個桶進行排序(一般用快排),然後合併成最後的結果。
8.2 圖解

8.3 核心程式
#include <stdio.h>
int main()
{
int a[11],i,j,t;
for(i=0;i<=10;i++)
a[i]=0; //初始化為0
for(i=1;i<=5;i++) //迴圈讀入5個數
{
scanf("%d",&t); //把每一個數讀到變數t中
a[t]++; //進行計數(核心行)
}
for(i=0;i<=10;i++) //依次判斷a[0]~a[10]
for(j=1;j<=a[i];j++) //出現了幾次就列印幾次
printf("%d ",i);
getchar();getchar();
//這裡的getchar();用來暫停程式,以便檢視程式輸出的內容
//也可以用system("pause");等來代替
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
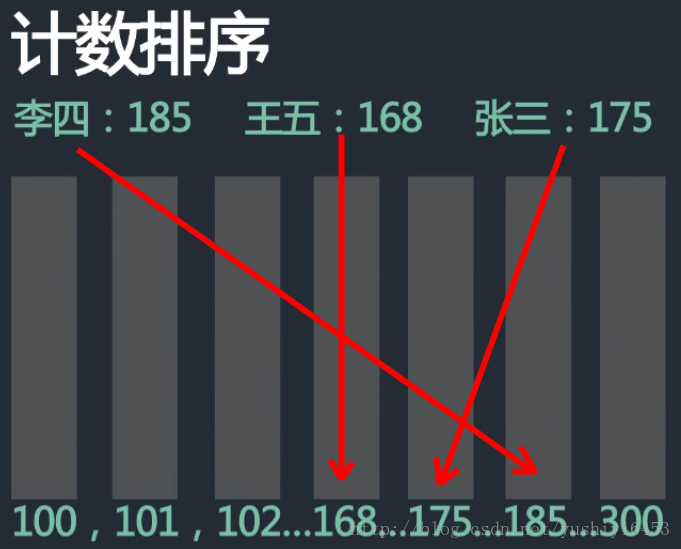
9 計數排序
9.1 過程
演算法的步驟如下:
- 找出待排序的陣列中最大和最小的元素
- 統計陣列中每個值為i的元素出現的次數,存入陣列C的第i項
- 對所有的計數累加(從C中的第一個元素開始,每一項和前一項相加)
- 反向填充目標陣列:將每個元素i放在新陣列的第C(i)項,每放一個元素就將C(i)減去1
9.2 圖解
9.3 核心程式(函式)
程式1:
#define NUM_RANGE (100) //預定義資料範圍上限,即K的值
void counting_sort(int *ini_arr, int *sorted_arr, int n) //所需空間為 2*n+k
{
int *count_arr = (int *)malloc(sizeof(int) * NUM_RANGE);
int i, j, k;
//初始化統計陣列元素為值為零
for(k=0; k<NUM_RANGE; k++){
count_arr[k] = 0;
}
//統計陣列中,每個元素出現的次數
for(i=0; i<n; i++){
count_arr[ini_arr[i]]++;
}
//統計陣列計數,每項存前N項和,這實質為排序過程
for(k=1; k<NUM_RANGE; k++){
count_arr[k] += count_arr[k-1];
}
//將計數排序結果轉化為陣列元素的真實排序結果
for(j=n-1 ; j>=0; j--){
int elem = ini_arr[j]; //取待排序元素
int index = count_arr[elem]-1; //待排序元素在有序陣列中的序號
sorted_arr[index] = elem; //將待排序元素存入結果陣列中
count_arr[elem]--; //修正排序結果,其實是針對算得元素的修正
}
free(count_arr);
}
程式2:C++(最大最小壓縮桶數)
public static void countSort(int[] arr) {
if (arr == null || arr.length < 2) {
return;
}
int min = arr[0];
int max = arr[0];
for (int i = 1; i < arr.length; i++) {
min = Math.min(arr[i], min);
max = Math.max(arr[i], max);
}
int[] countArr = new int[max - min + 1];
for (int i = 0; i < arr.length; i++) {
countArr[arr[i] - min]++;
}
int index = 0;
for (int i = 0; i < countArr.length; i++) {
while (countArr[i]-- > 0) {
arr[index++] = i + min;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
10 基數排序
10.1 過程
基數排序是基於資料位數的一種排序演算法。
它有兩種演算法
①LSD–Least Significant Digit first 從低位(個位)向高位排。
②MSD– Most Significant Digit first 從高位向低位(個位)排。
時間複雜度O(N*最大位數)。
空間複雜度O(N)。
10.2 圖解

對a[n]按照個位0~9進行桶排序:

對b[n]進行累加得到c[n],用於b[n]中重複元素計數
!!!b[n]中的元素為temp中的位置!!!跳躍的用++補上:

temp陣列為排序後的陣列,寫回a[n]。temp為按順序倒出桶中的資料(聯合b[n],c[n],a[n]得到),重複元素按順序輸出:
10.3 核心程式
//基數排序
//LSD 先以低位排,再以高位排
//MSD 先以高位排,再以低位排
void LSDSort(int *a, int n)
{
assert(a); //判斷a是否為空,也可以a為空||n<2返回
int digit = 0; //最大位數初始化
for (int i = 0; i < n; ++i)
{ //求最大位數
while (a[i] > (pow(10,digit))) //pow函式要包含標頭檔案math.h,pow(10,digit)=10^digit
{
digit++;
}
}
int flag = 1; //位數
for (int j = 1; j <= digit; ++j)
{
//建立陣列統計每個位出現數據次數(Digit[n]為桶排序b[n])
int Digit[10] = { 0 };
for (int i = 0; i < n; ++i)
{
Digit[(a[i] / flag)%10]++; //flag=1時為按個位桶排序
}
//建立陣列統計起始下標(BeginIndex[n]為個數累加c[n],用於記錄重複元素位置
//flag=1時,下標代表個位數值,數值代表位置,跳躍代表重複)
int BeginIndex[10] = { 0 };
for (int i = 1; i < 10; ++i)
{
//累加個數
BeginIndex[i] = BeginIndex[i - 1] + Digit[i - 1];
}
//建立輔助空間進行排序
//下面兩條可以用calloc函式實現
int *tmp = new int[n];
memset(tmp, 0, sizeof(int)*n);//初始化
//聯合各陣列求排序後的位置存在temp中
for (int i = 0; i < n; ++i)
{
int index = (a[i] / flag)%10; //桶排序和位置陣列中的下標
//計算temp相應位置對應a[i]中的元素,++為BeginIndex陣列數值加1
//跳躍間隔用++來補,先用再++
tmp[BeginIndex[index]++] = a[i];
}
//將資料重新寫回原空間
for (int i = 0; i < n; ++i)
{
a[i] = tmp[i];
}
flag = flag * 10;
delete[] tmp;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
附:
1 完整程式框架(氣泡排序舉例)
1.1 VS2010程式
#include "stdafx.h"
#include "stdio.h"
#include <stdlib.h>
void BubbleSort(int array[], int n){
int i,j,k,count1=0, count2=0;
for(i=0; i<n-1; i++)
for(j=n-1; j>i; j--)
{
count1++;
if(array[j-1]>array[j])
{
count2++;
k=array[j-1];
array[j-1]=array[j];
array[j]=k;
}
}
printf("總共的迴圈次序為:%d, 總共的交換次序為:%d\n\n", count1, count2);
}
int main(int argc, _TCHAR* argv[])
{
int as[]={0,1,2,3,4,6,8,5,9,7};
BubbleSort(as, 10);
for(int i=0; i<10; i++)
{
printf("%d", as[i]);
}
printf("\n\n");
system("pause");
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
1.2 執行程式(OJ)
#include <stdio.h>
void BubbleSort(int array[], int n){
int i,j,k,count1=0, count2=0;
for(i=0; i<n-1; i++)
for(j=n-1; j>i; j--)
{
count1++;
if(array[j-1]>array[j])
{
count2++;
k=array[j-1];
array[j-1]=array[j];
array[j]=k;
}
}
printf("總共的迴圈次序為:%d, 總共的交換次序為:%d\n\n", count1, count2);
}
int main()
{
int as[]={0,1,2,3,4,6,8,5,9,7};
BubbleSort(as, 10);
int i=0;
for(i=0; i<10; i++)
{
printf("%d", as[i]);
}
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
2 關於交換的優化
不用中間變數進行交換
if(A[j] <= A[i]){
A[j] = A[j] + A[i];
A[i] = A[j] - A[i];
A[j] = A[j] - A[i];
}
- 1
- 2
- 3
- 4
- 5
3 C語言實現陣列動態輸入
#include <stdio.h>
#include <assert.h> //斷言標頭檔案
#include <stdlib.h>
int main(int argc, char const *argv[])
{
int size = 0;
scanf("%d", &size); //首先輸入陣列個數
assert(size > 0); //判斷陣列個數是否非法
int *array = (int *)calloc(size, sizeof(int)); //動態分配陣列
if(!R1)
{
return; //申請空間失敗
}
int i = 0;
for (i = 0; i < size; ++i) {
scanf("%d", &array[i]);
}
mergeSort(array, size);
printArray(array, size);
free(array);
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
注:
1.colloc與malloc類似,但是主要的區別是儲存在已分配的記憶體空間中的值預設為0,使用malloc時,已分配的記憶體中可以是任意的值.
2.colloc需要兩個引數,第一個是需要分配記憶體的變數的個數,第二個是每個變數的大小.