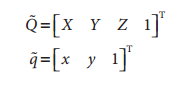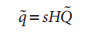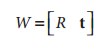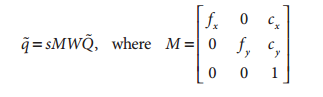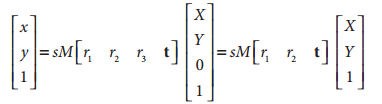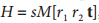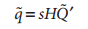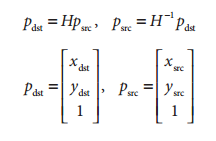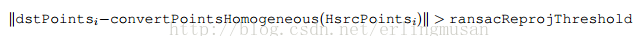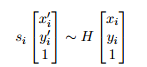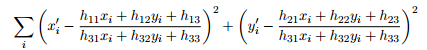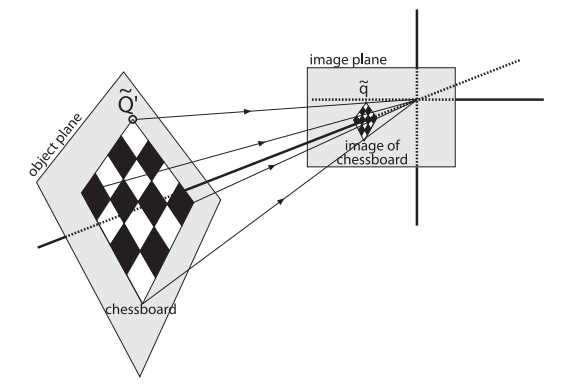
在計算機視覺中，平面的單應性被定義為一個平面到另外一個平面的投影對映。因此一個二維平面上的點對映到攝像機成像儀上的對映就是平面單應性的例子。如果點Q到成像儀上的點q的對映使用齊次座標，這種對映可以用矩陣相乘的方式表示。若有一下定義：

則可以將單應性簡單的表示為：

這裡引入引數s，它是任意尺度的比例（目的是使得單應性定義到該尺度比例）。通常根據習慣放在H的外面。

H有兩部分組成：用於定位觀察的物體平面的物理變換和使用攝像機內參數矩陣的投影。

物理變換部分是與觀測到的影象平面相關的部分旋轉R和部分平移t的影響之和，表示如下

這裡R為3*3大小的矩陣，t表示一個一個3維的列向量。

攝像機內參數矩陣用M表示，那麼我們重寫單應性如下：

我們知道單應性研究的是一個平面上到另外一個平面的對映，那麼上述公式中的~Q，就可以簡化為平面座標中的~Q'，即我們使Z=0。即物體平面上的點我們用x,y表示，相機平面上的點，我們也是用二維點表示。我們去掉了Z方向的座標，那麼相對於旋轉矩陣R，R可以分解為R=[r1 r2 r3]，那麼r3也就不要了，參考下面的推導：

其中H為：

是一個3×3大小的矩陣.

 故最終的單應性矩陣可表示如下：

OpenCV就是利用上述公式來計算單應性矩陣。它使用同一物體的多個影象來計算每個視場的旋轉和平移，同時也計算攝像機的內參數。我們知道旋轉和平移共6個引數，攝像機內參數為4個引數。對於每一個視場有6個要求解的新引數和4個不變的相機內參數。對於平面物體如棋盤，能夠提供8個方差，即對映一個正方形到四邊形可以用4個(x,y)來描述。那麼對於兩個視場，我們就有8*2=16=2*6+4,即求解所有的引數，至少需要兩個視場。

為什麼正方形到四邊形的四個點的對映可以確定8個方程呢，結果是顯然的，我們假設物體平面上的正方形的一個頂點座標為(u,v)，成像儀與該點對應的點座標為(x,y)，我們假設它們之間的關係如下：

u=f(x,y);

v=g(x,y);

顯然，我們把四點的對應座標帶入到上述公式可以得到8個方程。

這裡我們會想物體平面上正方形的四個頂點座標如何確定，其實我們就可以理解為角點的個數，對於尺度的話，我們有s進行控制。對於影象平面上的角點的位置，我們可以可以通過尋找角點來定位他們的位置。其實對於具體的操作，由於還沒細讀程式碼和相關原理，在這裡只能大體猜測一下。等日後學習了，再來糾正。

單應性矩陣H把源影象平面上的點集位置與目標影象平面上（通常是成像儀平面）的點集位置聯絡起來：

opencv就是利用多個視場計算多個單應性矩陣的方法來求解攝像機內參數。

OpenCV提供了一個方便的C函式cvFindHomography(),函式介面如下：

1. void cvFindHomography(  
2. const CvMat* src_points,  
3. const CvMat* dst_points,  
4. CvMat* homography  
5. );  

1. void cvFindHomography(  
2. const CvMat* src_points,  
3. const CvMat* dst_points,  
4. CvMat* homography  
5. );  

2、homography,為3*3大小的矩陣，用來儲存輸出的結果。

C++函式的介面：

1. Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,  
2. Mat& status, int method=0,  
3. double ransacReprojThreshold=3 );  
4. Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,  
5. vector<uchar>& status, int method=0,  
6. double ransacReprojThreshold=3 );  
7. Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,  
8. int method=0, double ransacReprojThreshold=3 );  

1. Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,  
2. Mat& status, int method=0,  
3. double ransacReprojThreshold=3 );  
4. Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,  
5. vector<uchar>& status, int method=0,  
6. double ransacReprojThreshold=3 );  
7. Mat findHomography( const Mat& srcPoints, const Mat& dstPoints,  
8. int method=0, double ransacReprojThreshold=3 );  

2、method:0表示使用所有點的常規方法；CV_RANSAC 基於RANSAC魯棒性的方法；CV_LMEDS 最小中值魯棒性方法

3、ransacReprojThreshod 僅在RANSAC方法中使用，一個點對被認為是內層圍值（非異常值）所允許的最大投影誤差。即如果：

那麼點i被認為是異常值。如果srcPoints和dstPoints單位是畫素，通常意味著在某些情況下這個引數的範圍在1到10之間。

4、status，可選的輸出掩碼，用在CV_RANSAC或者CV_LMEDS方法中。注意輸入掩碼將被忽略。

這個函式找到並且返回源影象平面和目的影象平面之間的透視變換矩陣H:

使得下面的返回投影誤差(back-projection)最小：

如果引數method設定為預設值0，該函式使用一個簡單的最小二乘方案來計算初始的單應性估計。

然而，如果不是所有的點對（srcPoints,dstPoints）都適應這個嚴格的透視變換。（也就是說，有一些異常值），這個初始估計值將很差。在這種情況下，我們可以使用兩個魯棒性演算法中的一個。RANSCA和LMEDS這兩個方法都嘗試不同的隨機的相對應點對的子集，每四對點集一組，使用這個子集和一個簡單的最小二乘演算法來估計單應性矩陣，然後計算得到單應性矩陣的質量quality/goodness。（對於RANSAC方法是內層圍點的數量，對於LMeDs是中間的重投影誤差）。然後最好的子集用來產生單應性矩陣的初始化估計和inliers/outliers的掩碼。

忽略方法，魯棒性與否，計算得到的單應性矩陣使用Levenberg-Marquardt方法來進一步減少重投影誤差，從而進一步提純。（對於魯棒性的方法僅使用內圍層點(inliers)）。

RANSAC方法，幾乎可以處理任含有何異常值比率的情況，但是它需要一個閾值用來區分inliers和outliers。LMeDS方法不需要任何閾值，但是它僅在inliers大於50%的情況下才能正確的工作。最後，如果你確信在你計算得到的特徵點僅含一些小的噪聲，但是沒有異常值，預設的方法可能是最好的選擇。（因此，在計算相機引數時，我們或許僅使用預設的方法）

這個函式用來找到初始化內參數和外引數矩陣。單應性矩陣取決於一個尺度，那麼通常歸一化，以使得h33=1。

[1] http://blog.csdn.net/yjl9122/article/details/50972320

[2] http://www.360doc.com/content/14/0410/14/10724725_367760906.shtml

[3] http://blog.csdn.net/jay463261929/article/details/53611363

[4] http://blog.csdn.net/sunshine_in_moon/article/details/45461819

[5] http://www.cnblogs.com/ml-cv/p/5871052.html

[6] http://blog.csdn.net/zinnc/article/details/52319491

[7] affine transformation: http://www.matongxue.com/madocs/244.html#/madoc