研究GBDT的背景是業務中使用到了該模型，用於做推薦場景，當然這裡就引出了GBDT的一個應用場景-迴歸，他的另外一個應用場景便是分類，接下來我會從以下幾個方面去學習和研究GBDT的相關知識，當然我也是學習者，只是把我理解到的整理出來。本文參考了網上各路大神的筆記，在此感謝！

Boosting&Bagging

整合學習方法不是單獨的一個機器學習演算法，而是通過構建多個機器學習演算法來達到一個強學習器。整合學習可以用來進行分類，迴歸，特徵選取和異常點檢測等。隨機森林演算法就是一個典型的整合學習方法，簡單的說就是由一個個弱分類器（決策樹）來構建一個強分類器，從而達到比較好的分類效果。

那麼如何得到單個的學習器，一般有兩種方法：

• 同質（對於一個強學習器而言，所用的單個弱學習器都是一樣的，比如說用的都是決策樹，或者都是神經網路）
• 異質（相對於同質而言，對於一個強學習器而言，所用的單個弱學習器不全是一樣的，比如說用的決策樹和神經網路的組合）

相對異質而言，同質學習期用的最為廣泛，我們平時所討論的整合學習方法指的就是同質個體學習器，同質個體學習器按照個體學習器之間的依賴關係分為序列（有強依賴關係）和並行（不存在關係或者有很弱的依賴關係），而在序列關係中有代表性的就是boosting系列演算法，並行關係中具有代表性的就是bagging和隨機森林（random forest）

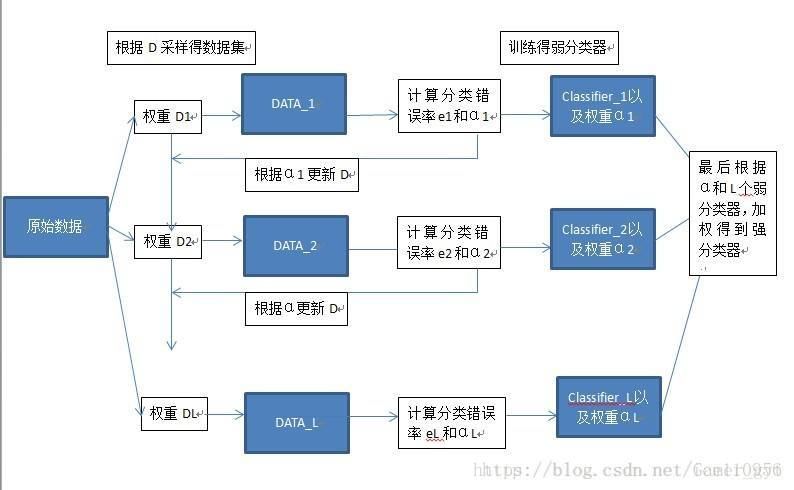
Boosting流程圖

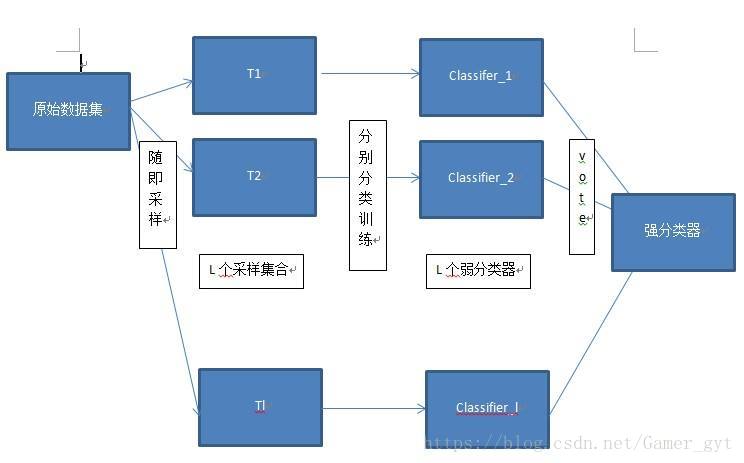
Bagging流程圖

上邊簡單的介紹了整合學習方法和boosting&bagging的區別，那麼對於單個學習器採用何種策略才能得到一個強學習器呢？

• 平均法（加權（個體學習器效能相差較大），簡單（效能相近））
• 投票法（絕對多數（超過半數標記。否則拒絕預測），相對多數，加權投票）
• 學習法（通過另一個學習器來進行結合，Stacking演算法）

Stacking演算法：
基本思想：先從初始資料集訓練出初級學習器，然後生成一個新資料集用於訓練次級學習器。在這個新資料集中，初級學習器的輸出被當作樣例輸入特徵，而出事樣本的標記仍被當作樣例標記。

注意點：若直接用初級學習器的訓練集來產生次級訓練集，則過擬合風險會比較大；一般會通過交叉驗證等方式，用訓練初級學習器未使用的樣本來產生次級學習器的訓練樣本。

Gradient Boosting

Gradient Boosting是一種Boosting的方法，它主要的思想是，每一次建立模型是在之前建立模型損失函式的梯度下降方向。損失函式是評價模型效能（一般為擬合程度+正則項），認為損失函式越小，效能越好。而讓損失函式持續下降，就能使得模型不斷改性提升效能，其最好的方法就是使損失函式沿著梯度方向下降（講道理梯度方向上下降最快）。

Gradient Boost是一個框架，裡面可以套入很多不同的演算法。

分類樹&迴歸樹&分類迴歸樹

分類樹

三種比較常見的分類決策樹分支劃分方式包括：ID3, C4.5, CART。

以C4.5分類樹為例，C4.5分類樹在每次分枝時，是窮舉每一個feature的每一個閾值，找到使得按照feature<=閾值，和feature>閾值分成的兩個分枝的熵最大的閾值(熵最大的概念可理解成儘可能每個分枝的男女比例都遠離1:1)，按照該標準分枝得到兩個新節點，用同樣方法繼續分枝直到所有人都被分入性別唯一的葉子節點，或達到預設的終止條件，若最終葉子節點中的性別不唯一，則以多數人的性別作為該葉子節點的性別。

總結：分類樹使用資訊增益或增益比率來劃分節點；每個節點樣本的類別情況投票決定測試樣本的類別。

迴歸樹

迴歸樹總體流程也是類似，區別在於，迴歸樹的每個節點（不一定是葉子節點）都會得一個預測值，以年齡為例，該預測值等於屬於這個節點的所有人年齡的平均值。分枝時窮舉每一個feature的每個閾值找最好的分割點，但衡量最好的標準不再是最大熵，而是最小化均方差即(每個人的年齡-預測年齡)^2 的總和 / N。也就是被預測出錯的人數越多，錯的越離譜，均方差就越大，通過最小化均方差能夠找到最可靠的分枝依據。分枝直到每個葉子節點上人的年齡都唯一或者達到預設的終止條件(如葉子個數上限)，若最終葉子節點上人的年齡不唯一，則以該節點上所有人的平均年齡做為該葉子節點的預測年齡。

總結：迴歸樹使用最大均方差劃分節點；每個節點樣本的均值作為測試樣本的迴歸預測值。

分類迴歸樹

Classification And Regression Trees，即既能做分類任務又能做迴歸任務，CART也是決策樹的一種，是一種二分決策樹，但是也可以用來做迴歸，CART同決策樹類似，不同於 ID3 與 C4.5 ,分類樹採用基尼指數來選擇最優的切分特徵，而且每次都是二分。至於怎麼利用基尼係數進行最優的特徵切分，大家可以參考這篇文章的詳細介紹 決策樹之 CART

損失函式

機器學習中的損失函式有很多，常見的有

• 0-1損失函式（0-1 loss function）
  L(Y,f(X))={1,Y≠f(X)0,Y=f(X)$$L(Y,f(X))=\{\begin{array}{r}1,Y\ne f(X)\\ 0,Y=f(X)\end{array}$$

該損失函式的意義就是，當預測錯誤時，損失函式值為1，預測正確時，損失函式值為0。該損失函式不考慮預測值和真實值的誤差程度，也就是隻要預測錯誤，預測錯誤差一點和差很多是一樣的。

• 平方損失函式（quadratic loss function）
  

  L(Y,f(X))=(Y−f(X))2$$L(Y,f(X))=(Y-f(X){)}^2$$

  取預測差距的平方

• 絕對值損失函式（absolute loss function）
  

  L(Y,f(X))=|Y−f(X)|$$L(Y,f(X))=|Y-f(X)|$$

  取預測值與真實值的差值絕對值，差距不會被平方放大

• 對數損失函式（logarithmic loss function）
  

  L(Y,P(Y|X))=−logP(Y|X)$$L(Y,P(Y|X))=-logP(Y|X)$$

  該損失函式用到了極大似然估計的思想。P(Y|X)通俗的解釋就是：在當前模型的基礎上，對於樣本X，其預測值為Y，也就是預測正確的概率。由於概率之間的同時滿足需要使用乘法，為了將其轉化為加法，我們將其取對數。最後由於是損失函式，所以預測正確的概率越高，其損失值應該是越小，因此再加個負號取個反。

• 全域性損失函式

  上面的損失函式僅僅是對於一個樣本來說的。而我們的優化目標函式應當是使全域性損失函式最小。因此，全域性損失函式往往是每個樣本的損失函式之和，即：
  

  J(w,b)=1m∑i=1mL(Y,f(X))$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L(Y,f(X))$$
  對於平方損失函式，為了求導方便，我們可以在前面乘上一個1/2，和平方項求導後的2抵消，即：
  J(w,b)=12m∑i=1mL(Y,f(X))$$J(w,b)=\frac{1}{2m}\sum _{i=1}^{m}L(Y,f(X))$$

• 邏輯迴歸中的損失函式
  

  在邏輯迴歸中，我們採用的是對數損失函式。由於邏輯迴歸是服從伯努利分佈(0-1分佈)的，並且邏輯迴歸返回的sigmoid值是處於(0,1)區間，不會取到0,1兩個端點。因此我們能夠將其損失函式寫成以下形式：
  L(y^,y)=−(ylogy^+(1−y)log(1−y^))$$L(\hat{y},y)=-(y\log \hat{y}+(1-y)\log (1-\hat{y}))$$

GBDT思想

以下部分學習於 GBDT演算法原理深入解析 ，原文作者講的很好，照搬過來，畢竟筆者不是推導數學公式的料，哈哈

GBDT 可以看成是由K棵樹組成的加法模型： y^i=∑k=1Kfk(xi),fk∈F(0)$$\begin{array}{}\text{(0)}& {\hat{y}}_i=\sum _{k=1}^K{f}_k(x_i),f_k\in F\end{array}$$ 其中F為所有樹組成的函式空間，以迴歸任務為例，迴歸樹可以看作為一個把特徵向量對映為某個score的函式。該模型的引數為：Θ={f1,f2,⋯,fK}$\mathrm{\Theta }=\{f_1,f_2,\cdots ,f_K\}$。於一般的機器學習演算法不同的是，加法模型不是學習d維空間中的權重，而是直接學習函式（決策樹）集合 上述加法模型的目標函式定義為：Obj=∑ni=1l(yi,y^i)+∑Kk=1Ω(fk)$Obj=\sum _{i=1}^{n}l(y_i,{\hat{y}}_i)+\sum _{k=1}^K\mathrm{\Omega }(f_k)$，其中