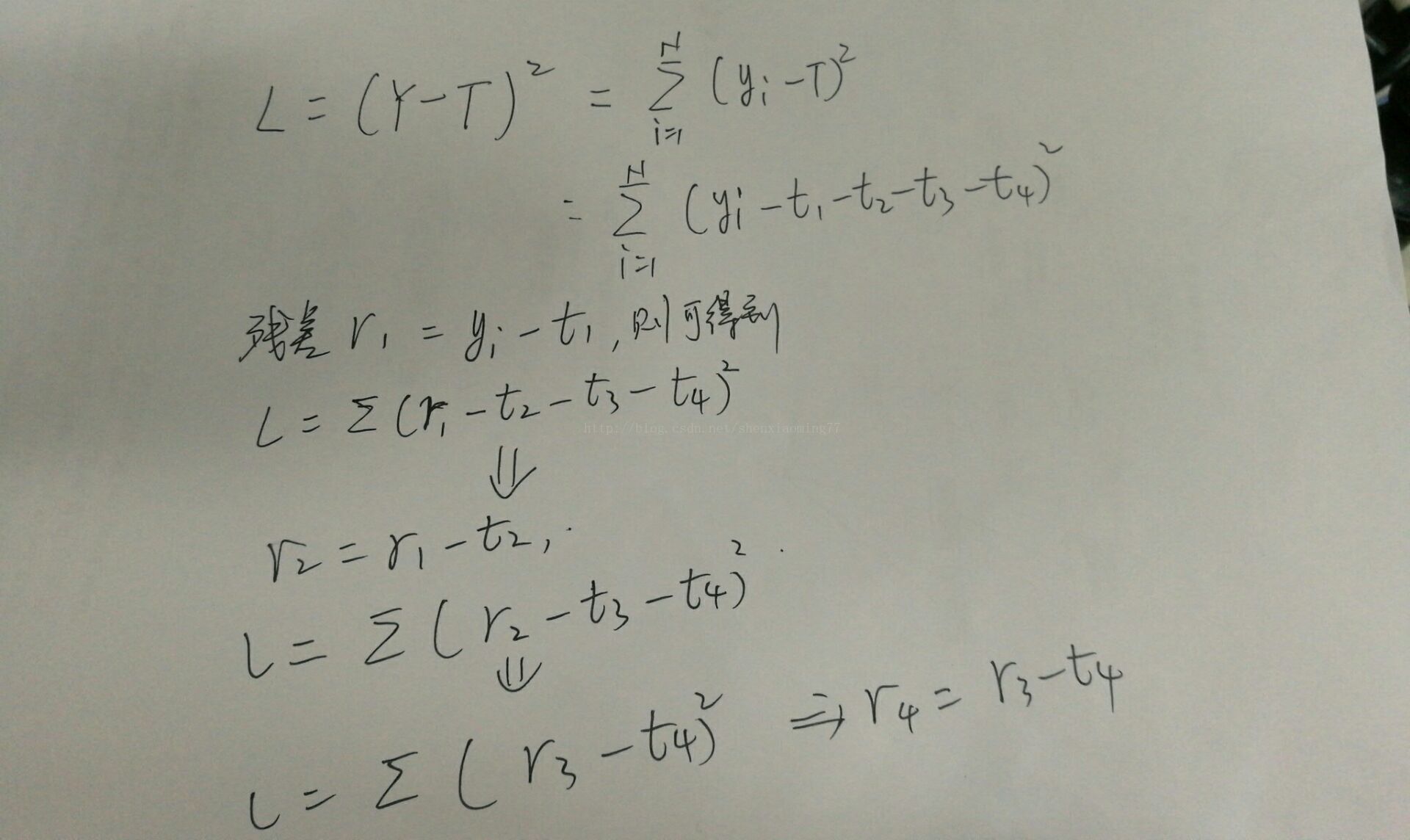GBDT 梯度提升決策樹的簡單推導
GB, 梯度提升,通過進行M次迭代,每次迭代產生一個迴歸樹模型,我們需要讓每次迭代生成的模型對訓練集的損失函式最小,而如何讓損失函式越來越小呢?我們採用梯度下降的方法,在每次迭代時通過向損失函式的負梯度方向移動來使得損失函式越來越小,這樣我們就可以得到越來越精確的模型。
假設GBDT模型T有4棵迴歸樹構成:t1,t2,t3,t4,樣本標籤為Y(y1,y2,y3,.....yn)
設定該模型的誤差函式為L,並且為SquaredError,則整體樣本的誤差推導如下:
對於首棵樹,可以看出,擬合的就是訓練樣本的標籤,並且得到t1預測後的殘差,從誤差函式的公式中可以看出,後面的殘差r2 = r1 - t2, r3 = r2 - t3, r4 = r3 - t4....,由此可以得出,後面的迴歸樹t2, t3, t4建立時 都是為了擬合前一次留下的殘差,可以看出,殘差不斷在減小,直至達到可接受的閾值為止。
對於梯度版本,採用誤差函式的當前負梯度值作為當前模型預測留下的殘差,因此建立新的一棵迴歸樹來擬合該殘差,更新後,整體gbdt模型的殘差將進一步降低,也帶來L的不斷降低
gbdt樹分為兩種,
(1)殘差版本
殘差其實就是真實值和預測值之間的差值,在學習的過程中,首先學習一顆迴歸樹,然後將“真實值-預測值”得到殘差,再把殘差作為一個學習目標,學習下一棵迴歸樹,依次類推,直到殘差小於某個接近0的閥值或迴歸樹數目達到某一閥值。其核心思想是每輪通過擬合殘差來降低損失函式。
總的來說,第一棵樹是正常的,之後所有的樹的決策全是由殘差來決定。
(2)梯度版本
與殘差版本把GBDT說成一個殘差迭代樹,認為每一棵迴歸樹都在學習前N-1棵樹的殘差不同,Gradient版本把GBDT說成一個梯度迭代樹,使用梯度下降法求解,認為每一棵迴歸樹在學習前N-1棵樹的梯度下降值。總的來說兩者相同之處在於,都是迭代迴歸樹,都是累加每顆樹結果作為最終結果(Multiple Additive
Regression Tree),每棵樹都在學習前N-1棵樹尚存的不足,從總體流程和輸入輸出上兩者是沒有區別的;
兩者的不同主要在於每步迭代時,是否使用Gradient作為求解方法。前者不用Gradient而是用殘差—-殘差是全域性最優值,Gradient是區域性最優方向*步長,即前者每一步都在試圖讓結果變成最好,後者則每步試圖讓結果更好一點。
兩者優缺點。看起來前者更科學一點–有絕對最優方向不學,為什麼捨近求遠去估計一個區域性最優方向呢?原因在於靈活性。前者最大問題是,由於它依賴殘差,cost function一般固定為反映殘差的均方差,因此很難處理純迴歸問題之外的問題。而後者求解方法為梯度下降,只要可求導的cost function都可以使用。