要求帶權有向圖中某一頂點到其他各頂點的最短路徑，常用Dijkstra演算法，該演算法基本思想是，先將圖的頂點分為兩個集合，一個為已求出最短路徑的終點集合（開始為原點v1），另一個為還未求出最短路徑的頂點集合（開始為除v1外的全部結點），然後按最短路徑長度的遞增順序逐個將第二個集合的頂點加到第一組中。

      
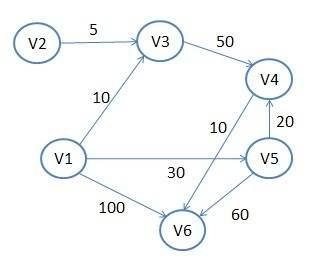
        演算法中使用dist陣列，dist[i]表示目前已經找到、v1到vi的當前最短路徑，否則為MAX；path陣列，作為是否找到該點最短路徑的標誌，path[i]==MIN表示為未找到，否則為最短路徑值。本例為方便，設定了下圖的測試用例。

具體演算法為

//Dijkstra求單源最短路徑
#include<stdio.h>
#define N 20 //圖的頂點最多數
#define MAX 1000
#define MIN -1
typedef int ElemType;//圖的頂點標識，這裡為自然數
//圖的結點結構
typedef struct ArcNode{
  ElemType adjvex;//圖的頂點 （該弧指向頂點的位置）
  struct ArcNode *nextarc;//指向下一條弧的指標
  int info//該弧權值
}ArcNode;
//表頭結點表
typedef struct VertexNode{
   ElemType data;
   ArcNode *firstarc;
}VertexNode;
//圖
typedef struct AdjList{
   VertexNode vertex[N];
   int vexnum;//圖的頂點數
   int arcnum;//弧數;
   int kind;//圖的種類（kind=1為有向圖）
   int dist[N];//圖的路徑長度
   int path[N];//輔助陣列
}AdjList;
//邊
typedef struct{
   int i;
   int j;
   int f;
}Side;
//鄰接表法建立圖
int CreateDAG(AdjList *L){
   int i,j;
   ArcNode *p=NULL;
   //測試用例
   Side S[N];
   S[0].i=1;S[0].j=3;S[0].f=10;
   S[1].i=1;S[1].j=5;S[1].f=30;
   S[2].i=1;S[2].j=6;S[2].f=100;
   S[3].i=2;S[3].j=3;S[3].f=5;
   S[4].i=3;S[4].j=4;S[4].f=50;
   S[5].i=4;S[5].j=6;S[5].f=10;
   S[6].i=5;S[6].j=6;S[6].f=60;
   S[7].i=5;S[7].j=4;S[7].f=20;
   for(i=1;i<7;i++){
      L->vertex[i].data=i;
      L->dist[i]=MAX;//設為最大值，表示不可達
      L->path[i]=MIN;//設為最小值，表示尚未初始化
      //L->vertex[i].indegree=0;
      L->vertex[i].firstarc=NULL;
   }
   L->kind=1;
   L->vexnum=6;
   L->arcnum=8;
   for(i=0;i<8;i++){
        p=(ArcNode *)malloc(sizeof(ArcNode));
        p->adjvex=S[i].j;
        p->info=S[i].f;
        p->nextarc=L->vertex[(S[i].i)].firstarc;
        L->vertex[(S[i].i)].firstarc=p;
        if(S[i].i==1){//初始頂點為1
            L->dist[(S[i].j)]=S[i].f;
            //L->path[(S[i].j)]=S[i].f;
        }
       // L->vertex[(S[i].j)].indegree++;
   }
   return 1;
}
//輸出鄰接表儲存
void PrintALGraph(AdjList *L){
   ArcNode *p=NULL;
   int i,k=0;
   for(i=1;i<=L->vexnum;i++){
      k=L->vertex[i].data;
      printf("V%d",k);
     // printf(" 入度為%d 鄰接點有 ",(L->vertex[i].indegree));
      p=L->vertex[k].firstarc;
      while(p!=NULL){
         printf(" ->%d",p->adjvex);
         p=p->nextarc;
      }
      printf("\n");
   }
}
//Dijkstra求單源最短路徑
void Dijkstra(AdjList *L){
   int i=1,j,k=0;
   Side s;
   L->path[1]=0;
   ArcNode *p=NULL;
   while(k<10){
    s.f=MAX;
    for(i=1;i<=L->vexnum;i++){
      if(L->path[i]!=MIN){
        p=L->vertex[i].firstarc;
        if(p!=NULL){
           while(p!=NULL){
              if(s.f>p->info&&L->path[(p->adjvex)]==MIN){
                 s.f=p->info;
                 s.i=i;
                 s.j=p->adjvex;
              }
              p=p->nextarc;
           }
        }
      }
    }
          if(s.f==MAX){

          }else if(L->dist[(s.j)]>L->dist[(s.i)]+s.f){
               L->dist[(s.j)]=L->dist[(s.i)]+s.f;
               L->path[(s.j)]=L->dist[(s.j)];
          }else{
               L->path[(s.j)]=L->dist[(s.j)];
          }
           k++;
   }
     //輸出
   printf("輸出最短路徑:\n");
   for(i=1;i<=L->vexnum;i++){
       if(L->dist[i]==1000||i==1){
         printf("v1到v%d不存在最短路徑\n",i);
       }else{
         printf("v1到v%d的最短路徑是%d\n",i,L->dist[i]);
       }
       printf("path is %d\n",L->path[i]);
   }
}
int main(){
   AdjList *L=(AdjList *)malloc(sizeof(AdjList));
   if(CreateDAG(L)==1){
        PrintALGraph(L);
        Dijkstra(L);
   }else{
      printf("建立失敗\n");
   }
}