【演算法課程實驗一】五種排序演算法的分析比較
實驗目的:
- 掌握選擇排序、氣泡排序、合併排序、快速排序、歸併排序的演算法原理
分析不同排序演算法的時間效率和時間複雜度,以及理論值與實測資料的對比分析。
一、氣泡排序
演算法虛擬碼:
for i=1 to n
for j=0 to n-i
if ( data[j]>=data[j+1])
swap(data[j],data[j+1])演算法思路:
第一個迴圈表示n-1趟即可完成排序。每一趟將最大的數調換位置到未排序數字的末尾。
資料分析:
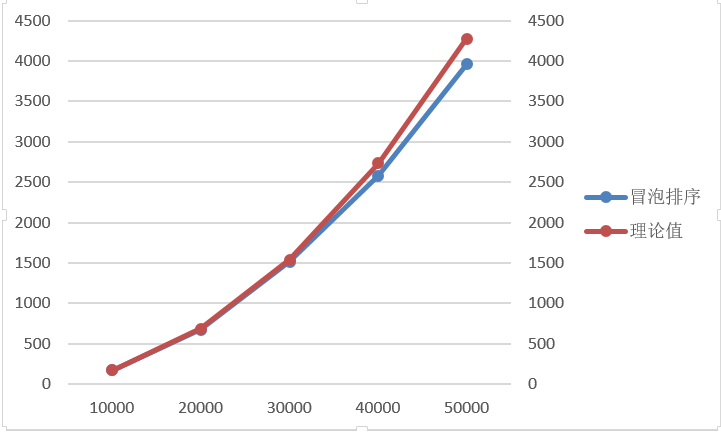
由圖1.氣泡排序的曲線圖可以看出氣泡排序的時間增長基本符合二次增長,先選取以n=10000的實際時間t1作為理論時間的基準。
當n=20000時,t2=t1*(2/1)2、
當n=30000時,t3=t1*(3/1)2,以此類推做出表1。
資料規模 | 10000 | 20000 | 30000 | 40000 | 50000 |
實際時間(ms) | 171.1 | 669.75 | 1513.8 | 2580.85 | 3956.85 |
理論時間 (ms) | 171 | 684 | 1539 | 2736 | 4275 |
表1.10000為基準
圖1.氣泡排序
由圖一可得,以n=10000為基準時,n=50000時理論和實際有一些偏差。懷疑是n=10000的實測時間可能是高於平均時長,所以我又以n=50000為基準做出下表。
資料規模 | 10000 | 20000 | 30000 | 40000 | 50000 |
實際時間(ms) | 171.1 | 669.75 | 1513.8 | 2580.85 | 3956.85 |
理論時間 (ms) | 158.274 | 633.096 | 1424.466 | 2532.384 | 3956.85 |
表2.以n=50000為基準
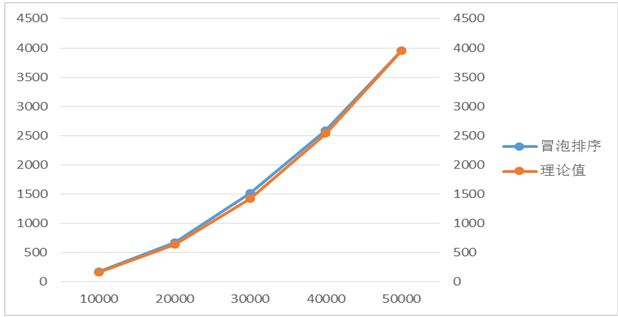 兩條曲線基本擬合,說明當n=10000時所測得的實際時間比平均時間略長一點,所以導致後面的理論值偏大。
兩條曲線基本擬合,說明當n=10000時所測得的實際時間比平均時間略長一點,所以導致後面的理論值偏大。時間複雜度分析:
氣泡排序最好情況:資料本來已是正序,僅需要進行n-1次比較操作即可,時間複雜度為O(n)
氣泡排序最壞情況:資料是倒序排列,需要進行次的比較操作,還需要進行3* n(n-1)/2次的賦值移動操作。時間複雜度為O(n2)
氣泡排序的平均時間複雜度:第i趟排序需要進行n-i次比較,一共要進行n-1趟排序,所以由求和公式得一共要進行n(n-1)/2次的比較操作,移動操作次數也在n2
二、選擇排序
演算法虛擬碼:
for i=0 to n-1{
k<-i
for j=k+1 to n-1{
if data[j]>data[k]
k<-j
}
If i!=k
Swap(data[i],data[k])
}演算法思路:
在未排序資料中找到最小值,放到起始位置當成已排序資料,然後再從剩餘序列中重複上述過程直到初始位置為陣列最末尾。
資料分析:
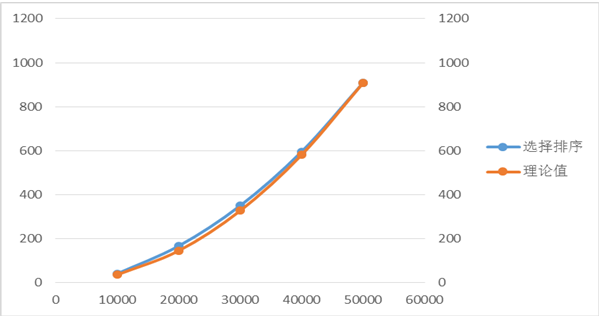
由圖2.選擇排序的曲線圖可以看出選擇排序的時間增長基本符合二次增長,先選取以n=10000的實際時間t1作為理論時間的基準。
當n=20000時,t2=t1*(2/1)2、
當n=30000時,t3=t1*(3/1)2,以此類推做出表3
資料規模 | 10000 | 20000 | 30000 | 40000 | 50000 |
實際時間(ms) | 41.25 | 167.1 | 350.15 | 595.75 | 908.65 |
理論時間 (ms) | 41.25 | 165 | 371.25 | 660 | 1031.23 |
表3.以10000為基準的選擇排序
由圖2看出當資料規模到達40000、50000時理論值與實際值的誤差較大,所以再以50000的實測時間作為基準,做出表4
資料規模 | 10000 | 20000 | 30000 | 40000 | 50000 |
實際時間(ms) | 41.25 | 167.1 | 350.15 | 595.75 | 908.65 |
理論時間 (ms) | 36.346 | 145.384 | 327.114 | 581.536 | 908.65 |
表4.以50000為基準的選擇排序
以50000實測時間為基準時做出的理論值預測更貼近實際時間,我認為n=10000的實測時間比平均時間略大,且由曲線貼合程度也能得出此結論。
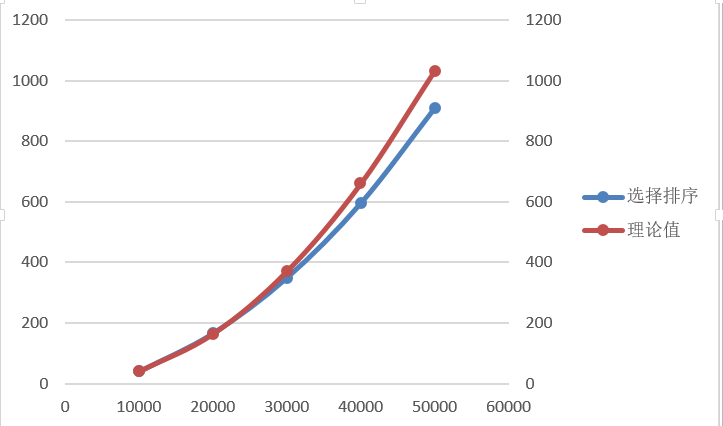
圖2.選擇排序
時間複雜度分析:
選擇排序最好情況:資料已經為正序,則需要進行n(n-1)/2次比較操作但是移動操作次數為0。
選擇排序最壞情況:資料為完全反序,則需要進行n(n-1)/2次比較操作和3(n-1)次移動操作。
選擇排序的平均時間複雜度:需要選擇n-1次最小數,第i次選擇時需要遍歷大小為n-i的陣列。所以比較操作一定需要進行n(n-1)/2次。所以無論移動次數進行多少次,平均時間複雜度為O(n2).
三、插入排序演算法虛擬碼:
for i=1 to n-1{
insertNode<-data[i]
for j=i-1 to 0 when insertNode<data[j]
data[j] move backward
data[j]<-insertNode
}演算法思路:
從第一個元素開始,此元素看做已排序元素,取出下一個元素向已排序元素中插入,從後向前掃描,直至所有元素插入已排序序列。就像打牌的時候,按牌的大小順序整理牌的過程。
資料分析:
由圖3.可以看出插入排序的時間增長也是基本符合二次增長,選取以n=10000的實際時間t1作為理論時間的基準。
當n=20000時,t2=t1*(2/1)2、
當n=30000時,t3=t1*(3/1)2,以此類推做出表5
資料規模 | 10000 | 20000 | 30000 | 40000 | 50000 |
實際時間(ms) | 18.2 | 79.6 | 173.75 | 287.5 | 471.35 |
理論時間 (ms) | 18.2 | 72.6 | 163.8 | 291.2 | 455 |
表5.以10000為基準
 圖3.插入排序
圖3.插入排序時間複雜度分析:
插入排序最好情況:資料為正序,則每次插入前僅需和前面一個數據比較,一共比較了n-1次,時間複雜度為O(n)。
插入排序最壞情況:資料為反序,則每次插入前要和前面的每一個數據比較,一共比較了n(n-1)/2次。時間複雜度為O(n2)
插入排序平均時間複雜度:平均情況下,在子陣列A[1..j-1]中的一半元素小於A[j],一半元素大於A[j],所以我們檢查子陣列A[1..j-1]的一半,假設最壞情況下檢查比較的次數為tj=j,則在這裡我們的比較次數為tj=j/2,所以平均情況和最壞情況同屬於O(n2)。
四、歸併排序
演算法虛擬碼:
Merge_Sort(data,low,high){
mid=(low+high)/2
if low< high{
Merge_Sort(data,low,mid)
Merge_Sort(data,mid+1,high)
Merge(data,low,mid,high)
}
}
Merge(data,low,mid,high){
i=low,j=mid+1
k=0
while i<=mid and j<=high{
if data[i]<data[j]
put data[i] into temp[k]
k++,i++
else
put data[j] into temp[k]
k++,j++
}
Put all rest elements into temp in order
}演算法思路:
將有n個待排元素的表看成n個已排好序的子表,然後進行兩兩歸併得到n/2個長度為2的有序子表,不斷兩兩歸併,直到歸併成一個長度為n的有序表。

資料分析:
選取以n=10000的實際時間t1作為理論時間的基準。
當n=20000時,t2≈t1*2
當n=30000時,t3≈t1*3,以此類推做出表6
資料規模 | 10000 | 20000 | 30000 | 40000 | 50000 |
實際時間(ms) | 2.4 | 5.1 | 8.2 | 10.2 | 12.4 |
理論時間 (ms) | 2.4 | 4.8 | 7.2 | 9.6 | 12 |
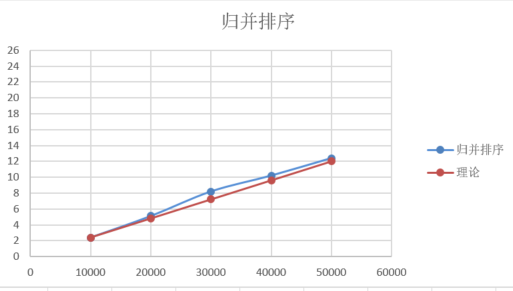
表6.歸併排序
時間複雜度分析:
歸併排序的遞迴樹形式如上圖所示,在自底向上的歸併過程中每一層需要進行n次的比較歸併操作。而樹的深度為nlogn,所以歸併排序的時間複雜度為O(nlogn)。
五、快速排序
演算法虛擬碼:
Quick_Sort(data,low,high){
If low>=high
return;
index=partition(data,low,high) #index是基準的下標
Quick_Sort(data,low,index-1)
Quick_Sort(data,index,high-1)
}
Int partition(data,low,high){
key=data[low]
While low<high{
While data[high]>=key and low<=high
high-- #直到遍歷完或者找到比基準小的值
data[low]=data[high] #把這個小值放到基準左邊
while data[low]<=key and low<=high
low++ #直到遍歷完或者找到比基準大的值
data[high]=data[low] #把這個大值放到基準右邊
}
data[high]=key
return high #返回基準值的位置
}演算法思路:
選取一個基準值,將比基準值大的元素移到基準右邊,比基準值小的移動到左邊,然後在左右兩個子集中,重複上述操作直到所有子集僅有一個元素。
資料分析:
選取以n=10000的實際時間t1作為理論時間的基準。
當n=20000時,t2≈t1*2
當n=30000時,t3≈t1*3,以此類推做出表7
資料規模 | 10000 | 20000 | 30000 | 40000 | 50000 |
實際時間(ms) | 1.32 | 2.3 | 4.05 | 5.3 | 7.4 |
理論時間 (ms) | 1.32 | 2.64 | 3.96 | 5.28 | 6.6 |
表7.10000為基準
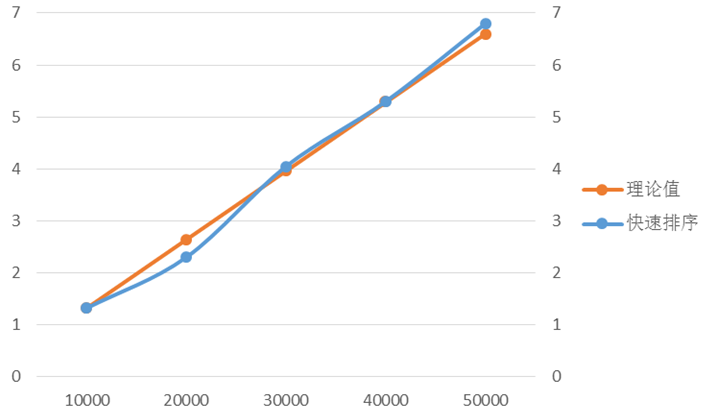
由圖五可以看出快速排序的時間增長基本符合線性增長的規律,且實測時間與理論時間曲線基本吻合,誤差都在0.1ms級別。
時間複雜度分析:快速排序的最好情況:每一次選取的基準都恰好為子集的中間值,則左右子集的元素個數基本一樣,則此時遞迴樹的深度為logn,在每一層中的比較次數都小於等於n,此時時間複雜度為O(nlogn)
快速排序的最壞情況:每一次選取的基準都恰好為子集中的最大或最小值,則子集的規模僅比原規模小1,所以需要做n-1次劃分。第i次劃分開始時,區間長度為n-i+1,所需的比較次數為 n-i。所以這種情況下比較次數達到最大值n(n-1)/2,所以此時時間複雜度為O(n2)。
快速排序的平均時間複雜度:最壞情況的產生與演算法或者是原待排陣列無關,所以快速排序的平均時間複雜度由遞迴樹方法可得為O(nlogn)。不考慮最壞情況的理由如下:每次劃分後左右兩個子集是無序的,每次選取子集第一個元素作為基準時,每一次此元素恰好是子集中的最值的概率非常小。
六、五種排序演算法的比較當資料規模從n=100變化到n=100W時,每種演算法的時間增長折線圖如下: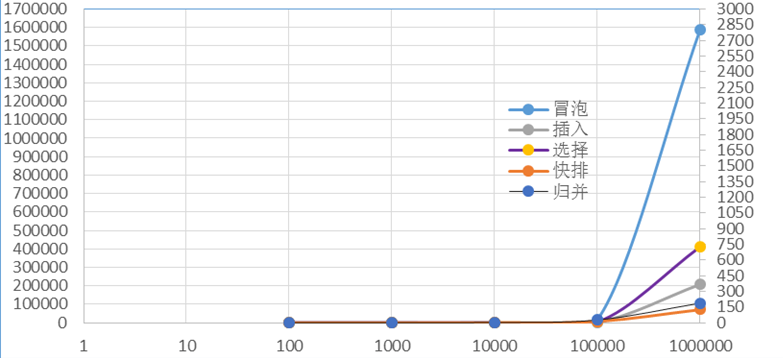
由圖可知:快排>歸併>插入>選擇>冒泡。
(1) 時間複雜度同為O(n2),為什麼又分快慢?
答:選擇排序快於氣泡排序是因為,氣泡排序的移動次數很多,每當發現前者大於後者的時候就需要進行交換,移動次數可以達到n2級別,而選擇排序最壞的情況下的移動次數也僅為3(n-1)次。
而插入排序比選擇排序要快的原因則是每一趟選擇排序要在剩下的資料中找到最小元素,則第i趟排序必須需要進行n-i次的比較。而插入排序將新元素插入到已排好序列中時,不一定每一次都要與前面的每一個元素進行比較,除非每一次要插入的元素比已排好序列中的每個值都小,所以插入排序要快於選擇排序。
(2) 時間複雜度同為O(nlogn),為什麼快排更快呢?
答:快速排序快在資料賦值操作少。在歸併排序中,每兩個子集合並時都要將兩子集中所有元素寫入到新陣列中儲存。則在每一層的歸併中資料的寫入操作一定為n。而在快速排序中,每一個子集中,並不需要移動每一個元素,因為很多比基準小的元素本來就在基準左邊,比基準大的元素本來就在基準右邊。所以同為O(nlogn),快速排序又更勝一籌。