機器學習中經常遇到這幾個概念，用大白話解釋一下：

一、歸一化

把幾個數量級不同的資料，放在一起比較（或者畫在一個數軸上），比如：一條河的長度幾千甚至上萬km，與一個人的高度1.7m，放在一起，人的高度幾乎可以被忽略，所以為了方便比較，縮小他們的差距，但又能看出二者的大小關係，可以找一個方法進行轉換。

另外，在多分類預測時，比如：一張圖，要預測它是貓，或是狗，或是人，或是其它什麼，每個分類都有一個預測的概率，比如是貓的概率是0.7，狗的概率是0.1，人的概率是0.2... , 概率通常是0到1之間的數字，如果我們算出的結果，不在這個範圍，比如：700，10，2 ，甚至負數，這樣就需要找個方法，將其轉換成0-1之間的概率小數，而且通常為了滿足統計分佈，這些概率的和，應該是1。

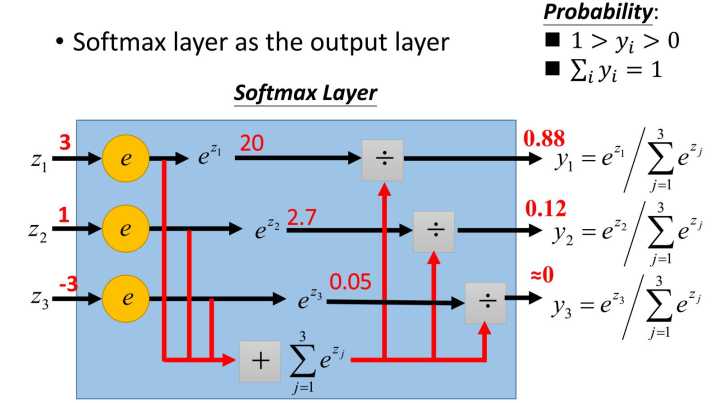
最常用的處理方法，就是softmax，原理如上圖（網上淘來的）。

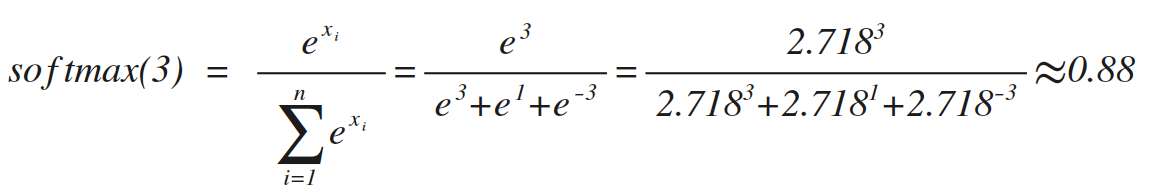
類似的softmax(1)=0.12，softmax(-3)=0，這個方法在數學上沒毛病，但是在實際運用中，如果目標值x很大，比如10000，那e的10000次方，很可能超出程式語言的表示範圍，所以通常做softmax前，要對資料做一下預處理（比如：對於分類預測，最簡單的辦法，所有訓練集整體按比例縮小） 

二、資訊熵

熱力學中的熱熵是表示分子狀態混亂程度的物理量，而且還有一個所謂『熵增原理』，即：宇宙中的熵總是增加的，換句話說，分子狀態總是從有序變成無序，熱量總是從高溫部分向低溫部分傳遞。 夏農借用了這個概念，用資訊熵來描述信源的不確定度。

簡單點說，一個資訊源越不確定，裡面蘊含的資訊量越大。舉個例子：吳京《戰狼2》大獲成功後，說要續拍《戰狼3》，但是沒說誰當女主角，於是就有各種猜測，各種可能性，即：資訊量很大。但是沒過多久，吳京宣佈女主角確定後，大家就不用再猜測女主角了，資訊量相比就沒這麼大了。

這個例子中，每種猜測的可能性其實就是概率，而資訊量如何衡量，可以用下面的公式來量化計算，算出來的值即資訊熵：

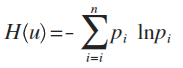
這裡p為概率，最後算出來的結果通常以bit為單位。

舉例：拿計算機領域最常現的編碼問題來說，如果有A、B、C、D這四個字元組成的內容，每個字元出現的概率都是1/4，即概率分佈為{1/4，1/4，1/4，1/4}，設計一個最短的編碼方案來表示一組資料，套用剛才的公式：

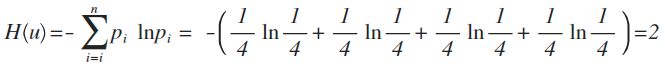
即：2個bit，其實不用算也能想明白，如果第1位0表示A，1表示B；第2位0表示C，1表示D，2位編碼搞定。

如果概率變了，比如A、B、C、D出現的概率是{1，1，1/2，1/2}，即：每次A、B必然出現，C、D出現機會各佔一半，這樣只要1位就可以了。1表示C，0表示D，因為AB必然出現，不用表示都知道肯定要附加上AB，套用公式算出來的結果也是如此。

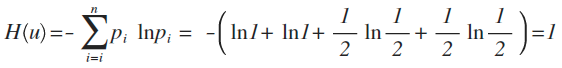
三、交叉熵 

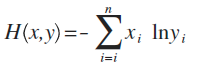
這是公式定義，x、y都是表示概率分佈（注：也有很多文章喜歡用p、q來表示），這個東西能幹嘛呢？

假設x是正確的概率分佈，而y是我們預測出來的概率分佈，這個公式算出來的結果，表示y與正確答案x之間的錯誤程度（即：y錯得有多離譜），結果值越小，表示y越準確，與x越接近。

比如：

x的概率分佈為：{1/4 ，1/4，1/4，1/4}，現在我們通過機器學習，預測出來二組值：

y1的概率分佈為  {1/4 ,  1/2 , 1/8 , 1/8}

y2的概率分佈為  {1/4 ,  1/4 , 1/8 , 3/8}

從直覺上看，y2分佈中，前2項都100%預測對了，而y1只有第1項100%對，所以y2感覺更準確，看看公式算下來，是不是符合直覺：

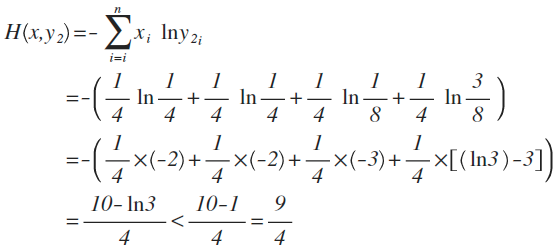
對比結果，H(x,y1)算出來的值為9/4，而H(x,y2)的值略小於9/4，根據剛才的解釋，交叉熵越小，表示這二個分佈越接近，所以機器學習中，經常拿交叉熵來做為損失函式(loss function)。 

參考文章：

https://www.zhihu.com/question/23765351
https://www.zhihu.com/question/41252833/answer/108777563
https://www.zhihu.com/question/22178202