好的特徵應該具有以下幾個特點：

• 重複性：不同影象相同的區域應該能被重複檢測到，而且不受到旋轉、模糊、光照等因素的影響；
• 可區分性：不同的檢測子，應該可以被區分出來，而為了區分它們，應運而生的就是與檢測對應的描述子了；
• 數量適宜：檢測子可別太多，不然啥阿貓阿狗都能出來混，但也不能太少，要求太高可就招不到人才了；
• 高定位（尺度和位置）：是在哪出現的，最好就在哪被找到，可別跑偏了；
• 有效性：檢測速度越快越好。

這次來介紹下SURF區域性特徵點檢測與匹配~

Surf是對David Lowe在1999年提出的Sift演算法的改進，提升了演算法的執行效率，為演算法在實時計算機視覺系統中應用提供了可能。與Sift演算法一樣，Surf演算法的基本路程可以分為三大部分：區域性特徵點的提取、特徵點的描述、特徵點的匹配。

但Surf在執行效率上有兩大制勝法寶——一個是積分圖在Hessian（海森矩陣）上的使用，一個是降維的特徵描述子的使用。瞭解這兩大法寶是如何出奇制勝前，先回顧一下傳統Sift演算法的基本思路及其優缺點。

Sift是一種基於尺度空間的，對影象縮放、旋轉、甚至仿射變換保持不變性的影象區域性特徵描述運算元。

一、特徵點提取

Sift的特徵點是在DOG金字塔尺度空間中提取的，尺度空間的構建涉及到高斯卷積、影象下采樣和高斯差分操作。在尺度空間中先初步提取出在尺度空間和二維影象空間上都是區域性極值點的興趣點，再濾除掉能量低的不穩定的和錯誤的興趣點，得到最終穩定的特徵點。

二、特徵點描述

特徵點描述包括特徵點方向分配和128維向量描述兩個步驟。

特徵的的方向分配：Sift求取特徵點周圍鄰域內所有畫素的梯度方向，生成梯度方向直方圖，並歸一化為0~360°的梯度方向直方圖到36個方向內，取梯度直方圖的主要分量所代表的方向作為特徵點的方向。

128維向量描述：這個仍然是基於梯度方向直方圖展開的，去特徵點周圍鄰域4*4個快，每塊提取出8個梯度方向，共計128個方向作為特徵的描述子。

三、特徵點的匹配

特徵點的匹配是通過計算兩組特徵點的128維的特徵點的歐氏距離實現的。歐氏距離越小，則相似度越高，當歐式距離小於設定閾值時，可以判定為匹配成功。

Sift演算法的優點是特徵穩定，對旋轉、尺度變換、亮度保持不變性，對視角變換、噪聲也有一定程度的穩定性；缺點是實時性不高，並且對於邊緣光滑目標的特徵點提取能力較弱。

Surf改進了特徵的提取和描述方式，用一種更為高效的方式完成特徵的提取和描述，具體實現流程如下：

1. 構建Hessian（海森矩陣），生成所有的興趣點，用於特徵的提取；
2. 構建尺度空間
3. 特徵點定位
4. 特徵點主方向分配
5. 生成特徵點描述子
6. 特徵點匹配

1. 構建Hessian（海森矩陣），生成所有的興趣點，用於特徵的提取；

構建Hessian矩陣的目的是為了生成影象穩定的邊緣點（突變點），跟Canny、拉普拉斯邊緣檢測的作用類似，為下文的特徵提取做好基礎。構建Hessian矩陣的過程對應於Sift演算法中的高斯卷積過程。

海森矩陣（Hessian Matrix）是一個多元函式的二階偏導數構成的方陣，描述了函式的局部曲率。由德國數學家Ludwin Otto Hessian於19世紀提出。

對一個影象f（x，y），其Hessian矩陣如下：

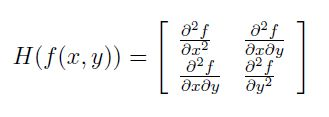
在構造Hessian矩陣前需要對影象進行高斯濾波，經過濾波後的Hessian矩陣表述為：

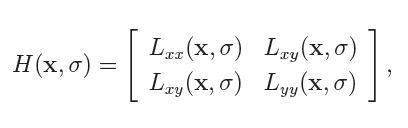
當Hessian矩陣的判別式取得區域性極大值時，判定當前點是比周圍鄰域內其他點更亮或更暗的點，由此來定位關鍵點的位置。

我們知道在離散數字影象中，一階導數是相鄰畫素的灰度差：

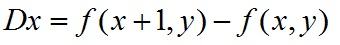
二階導數是對一階導數的再次求導：

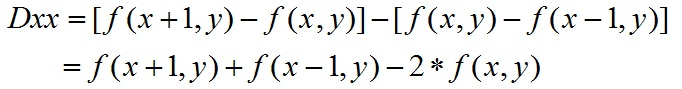
反過來看Hessian矩陣的判別式，其實就是當前點對瓶方向二階偏導乘以垂直方向的二階偏導再減去當前點水平、垂直二階偏導的二次方：

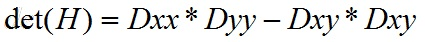
Hessian矩陣判別式中的f（x，y）是原始影象的高斯卷積，由於高斯核實服從正態分佈的，從中心點往外，係數越來越低，為了提高運算速度，Surf使用了盒式濾波器來近似替代高斯濾波器，所以在Dxy上乘了一個加權係數0.9，目的是為了平衡因使用盒式濾波器近似所帶來的誤差：

高斯濾波器和盒式濾波器的示意圖如下：

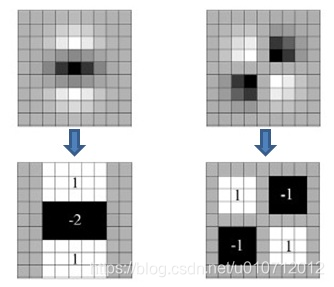
上邊兩幅圖是9*9高斯濾波器模板分別在影象上垂直方向上二階導數Dyy和Dxy對應的值，下邊兩幅圖是使用盒式濾波器對其近似，灰色部分的畫素值為0，黑色為-2，白色為1。

那麼為什麼盒式濾波器可以提高運算速度呢，這就涉及到積分圖的使用。盒式濾波器對影象的濾波轉化成計算影象上不同區域間畫素和的加減運算問題，這正是積分圖的強項，只需要簡單幾次查詢積分圖就可以完成。

2. 構建尺度空間
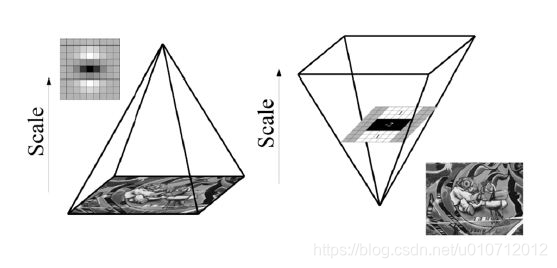
同Sift一樣，Surf的尺度空間也是由Octave(金字塔的層)組成，不同的是，Sift中下一組影象的尺寸是上一組的一半，同一組間影象尺寸一樣，但是所使用的高斯模糊係數逐漸增大；而在Surf中，不同組間影象的尺寸都是一致的，不同的是不同組間使用的盒式濾波器的模板尺寸逐漸增大，同一組間不同層間使用相同尺寸的濾波器，但是濾波器的模糊係數逐漸增大，如下圖所示：

3. 特徵點定位（利用非極大抑制初步確定特徵點，再精確定位）

特徵點的定位過程Surf和Sift保持一致，將經過Hessian矩陣處理的每個畫素點與二維影象空間和尺度空間鄰域內的26個點進行比較，初步定位出關鍵點，再經過濾除能量比較弱的關鍵點以及錯誤定位的關鍵點，篩選出最終的穩定的特徵點。

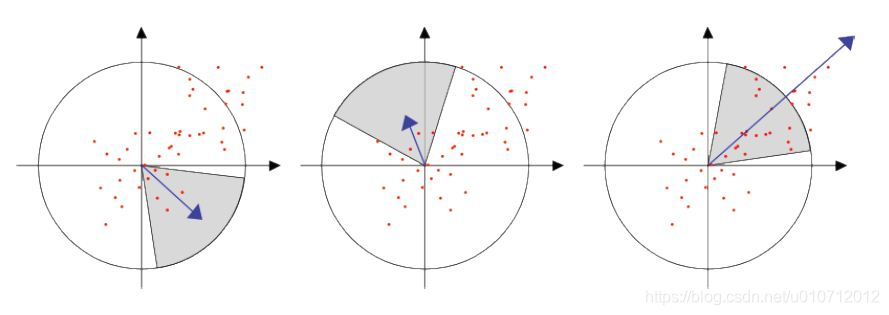
4. 特徵點主方向分配

Sift特徵點方向分配是採用在特徵點鄰域內統計其梯度直方圖，取直方圖bin值最大的以及超過最大bin值80%的那些方向作為特徵點的主方向。而在Surf中，採用的是統計特徵點圓形鄰域內的harr小波特徵。即在特徵點的圓形鄰域內，統計60度扇形內所有點的水平、垂直haar小波特徵總和，然後扇形以0.2弧度大小的間隔進行旋轉並再次統計該區域內haar小波特徵值之後，最後將值最大的那個扇形的方向作為該特徵點的主方向。該過程示意圖如下：

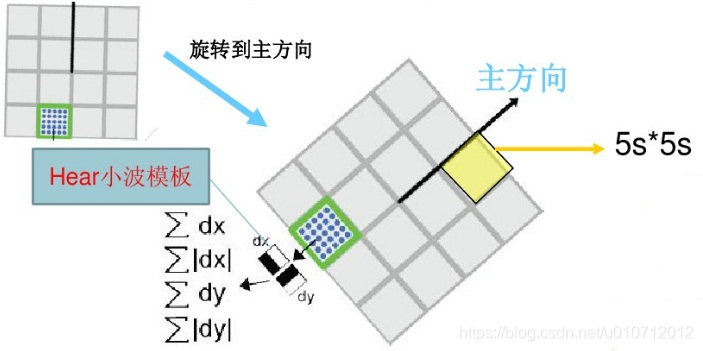
5. 生成特徵點描述子

在Sift中，是取特徵點周圍44個區域塊，統計每小塊內8個梯度方向，用著44*8=128維向量作為Sift特徵的描述子。

Surf演算法中，也是在特徵點周圍取一個4*4的矩形區域塊，但是所取得矩形區域方向是沿著特徵點的主方向。每個子區域統計25個畫素的水平方向和垂直方向的haar小波特徵，這裡的水平和垂直方向都是相對主方向而言的。該haar小波特徵為水平方向值之和、垂直方向值之和、水平方向絕對值之和以及垂直方向絕對值之和4個方向。該過程示意圖如下：

6. 特徵點匹配

與Sift特徵點匹配類似，Surf也是通過計算兩個特徵點間的歐式距離來確定匹配度，歐氏距離越短，代表兩個特徵點的匹配度越好。不同的是Surf還加入了Hessian矩陣跡的判斷，如果兩個特徵點的矩陣跡正負號相同，代表這兩個特徵具有相同方向上的對比度變化，如果不同，說明這兩個特徵點的對比度變化方向是相反的，即使歐氏距離為0，也直接予以排除。

本來想在visual studio上跑surf演算法進行影象特徵點匹配的，但是，SURF/SIFT演算法在opencv3.X中是沒有的，需要下載opencv_contrib擴充套件庫，之後需要用cmake進行編譯，但是我按照教程做了，還是不能用，顯示不能使用SURF，搞了一天還沒搞定，一氣之下，人生苦短，我用python。在python下搞opencv。