本文先給出假設檢驗和抽樣分佈的定義，然後，以一個正態總體的均值抽樣分佈為例，介紹假設檢驗的過程，最後拓展到其他抽樣分佈的情況並總結。

1 假設檢驗

假設檢驗（hypothesis test）又稱為顯著性檢驗（significance test），是根據總體的理論分佈和小概率理論，對未知或不完全知道的總體提出兩種彼此對立的假設，然後由樣本的實際結果，經過一定的計算，作出在一定概率意義上應該接受的那種假設的推斷。如果抽樣結果使小概率事件發生，則拒絕假設；如果抽樣結果沒有使小概率事件發生，則接受假設。

2 抽樣分佈

定義：從一個總體中，獨立隨機地抽取一定數目的樣本，所得到的樣本各種統計量的概率分佈。

2.1 舉例說明抽樣分佈的實際含義

假設現在有一個年級的學生，我們每次從中隨機抽取10名學生，測量身高，計算它們的均值。重複上面的操作50次。這樣，我們就得到了50個均值，然後我們可以畫出均值的頻率分佈圖。這就是一個抽樣分佈。

3 一個正態總體均值的抽樣分佈 & 假設檢驗

在統計學中，常常假設總體是服從正態分佈的。因為基於這個條件，抽樣分佈的性質很明確。

如果從一個總體N(μ,σ2)中獨立隨機地抽取n個樣本，那麼X¯∼N(μ,σ2n)，也寫做X¯−μσ/n√∼N(0,1)。

這個的定義是什麼意思呢？舉個例子，自變數X的值服從正態分佈N(μ,σ2)。如圖1所示，就是指X變數取不同數值的概率是一個正態函式。然後，隨機取值n

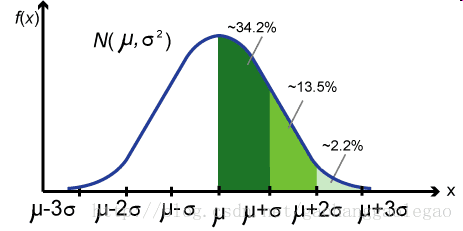
圖1 正態分佈

趁熱打鐵，舉一個例題。
根據長期的經驗和資料的分析，某磚瓦廠所生產的磚的“抗斷強度”服從正態分佈，方差σ2=1.21。現在從該廠生產的一批磚中，隨機抽取6塊，測得抗斷強度（kg/cm2）如下：
32.56 29.66 31.64 30.00 31.87 31.03
問這一批磚的平均抗斷強度可否認為是32.50（kg/cm2）？

首先，我們得做出對總體的假設。這裡，總體就是那一批磚，樣本就是隨機抽取出來的6塊磚。所以，我們提出假設H0: 可以認為那一批磚的平均抗斷強度為32.50。H1: 不可以認為平均抗斷強度為32.50。

在假設之後，我們就有了總體正態分佈N(μ,σ2)的引數μ=32.50，σ2=1.21。根據前面的知識，我們也知道抽樣的均值也服從正態分佈X∼N(μ,σ2n)，即X¯∼N(32.5,0.2)，如圖2所示。

圖2 均值的抽樣分佈函式

接著，就到了檢驗的環節了。如果總體的情況真的是這樣，那麼這組實際抽樣得到資料是不是很合理呢？在這裡，就是指，這組資料的平均值不是離中心值32.50比較近。
我們來算一算這組資料的平均值。

在圖2中，就是紅色線代表的位置。直觀的感覺，並不是很大的概率會出現這樣的結果，因為在紅色線左邊的面積很小，意味著出現這個數值的可能性很小。

總結成一段話：抽樣分佈是我們用來對假設進行檢驗的工具，在不同情況下，我們需要使用不同的工具，但是思路都是一致的。當我們對總體提出假設後，理論上的抽樣分佈就已經得到了，然後，我們要做的就是計算樣本的資料的出現是否屬於小概率事件。如果是，我們就否定原假設；如果不是，則保留原假設。