增量構造演算法

每次遞迴選取一個值放入到集合中，每次遞迴也輸出一遍
遞迴結束就是無法向集合中新增元素時

#include <iostream>
using namespace std;
//cur用於確定子集的大小
void print_subset(int *A,int n,int cur)
{
    if(cur==0) cout << "kong";
    for(int i = 0;i<cur;i++)//輸出當前子集
        cout << A[i] + 1 << " ";
    cout << endl;
    int
 
 s = cur? A[cur-1]+1 : 0;//獲取當前子集的最小值，當cur為0時防止出現A[-1]
    for(int i=s;i<n;i++)//每一次迴圈都存入一個不同的數進集合，此時變生成了不同的子集
    {
        A[cur]=i;
        print_subset(A,n,cur+1);
    }
}

int main()
{
    int n;
    cout<<"輸入n"<<endl;
    while(cin >> n)
    {
        int *A=new int[n + 1];
        for
 
(int i = 1; i <= n; ++ i)
            A[i] = i;
        print_subset(A,n,0);
    }
    return 0;
}

位向量法

對一個含有n個元素的集合構造一個大小也為n的布林陣列，若陣列的值為true，則說明該子集包含該元素。（與布林值組合類似）

#include <iostream>

using namespace std;

int print_subset(char *A, bool *B, int cur,int n)
{
    if(cur==n)//當設定完布林陣列內的全部元素後輸出
 

    {
        for(int i = 0; i<n;i++)
        {
            if(B[i])
                cout << A[i];
        }
        cout << endl;
    }
    else
    {
        B[cur] = true;//選第cur個元素
        print_subset(A,B,cur + 1,n);
        B[cur] = false;//不選第cur個元素
        print_subset(A,B,cur + 1,n);
    }
}

int main()
{
    char a[] = {'a','b','c'};
    bool *b = new bool(3);
    int n=3;
    print_subset(a,b,0,n);
    return 0;
}

二進位制法

用一個二進位制數來表示一個集合。例如，110110就可以表示{5,4,2,1,}（1說明包含元素，0表示不包含,從右往左依次為0,1,2…..）
二進位制的運算

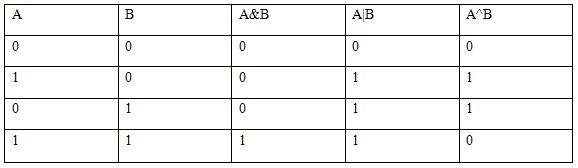
位運算子是逐位進行運算的，兩個32位整數進行位運算相當於32對0/1值進行運算，對於集合來說，相當於交，並，對稱差運算。

所以便可以利用二進位制來表示一個集合然後列舉子集

#include <iostream>

using namespace std;

void print_subset(int n,int s)//輸出子集s包含的元素
{
    for(int i=0;i<n;i++)
    {
        //<<把一個整型數的所有位向左移動指定的位數，移動到左邊界之外的多餘二進位制位會被丟棄，並從右邊界移入0
        if(s&(1<<i))//從最右側開始遍歷s中是否含有相應的元素
            cout << i+1 << " ";
    }
    cout << endl;

}

int main()
{
    int n=3;
    for(int i=0;i<(1<<n);i++)//設定二進位制數的長度，列舉子集
        print_subset(3,i);
    return 0;
}