Ⅱ、預備知識

樹鏈剖分，又叫重鏈剖分，樹剖。顧名思義，就是在樹上將樹劃分為一條條鏈，然後進行樹上修改與查詢操作(針對於結點操作，邊權操作後面會講)，用線段樹來維護保證時間復雜度(數據結構模板)。一般來說，可以支持以下幾種操作：
1、樹上路徑區間修改
2、樹上路徑間的區間查詢(如點權之和，最大值等)
講道理實際上線段樹能做的它在樹上都能做QAQ
接下來進入毒瘤內容

Ⅲ、拋出問題

先看一道板子

題目描述

如題，已知一棵包含N個結點的樹（連通且無環），每個節點上包含一個數值，需要支持以下操作：
操作1：格式：1 x y z 表示將樹從x到y結點最短路徑上所有節點的值都加上z
操作2：格式：2 x y 表示求樹從x到y結點最短路徑上所有節點的值之和

輸入輸出格式

輸入格式：

第一行包含4個正整數N、M、R、P，分別表示樹的結點個數、操作個數、根節點序號和取模數（即所有的輸出結果均對此取模）。
接下來一行包含N個非負整數，分別依次表示各個節點上初始的數值。
接下來N-1行每行包含兩個整數x、y，表示點x和點y之間連有一條邊（保證無環且連通）
接下來M行每行包含若幹個正整數，每行表示一個操作，格式如下：
操作1： 1 x y z
操作2： 2 x y
操作3： 3 x z
操作4： 4 x

輸出格式：

輸出包含若幹行，分別依次表示每個操作2或操作4所得的結果（對P取模）

輸入輸出樣例

輸入樣例#1：

5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

輸出樣例#1：

2
21

說明：

時空限制：1s，128M
數據規模：
對於30%的數據：\(N\leq 10,M\leq 10\)
對於70%的數據：\(N\leq{10}^3,M\leq{10}^3\)
對於100%的數據：\(N\leq{10}^5,M\leq{10}^5\)
（其實，純隨機生成的樹LCA+暴力是能過的，可是，你覺得可能是純隨機的麽233）
樣例說明：
樹的結構如下：

各個操作如下：

故輸出應依次為2、21(重要的事情說三遍：記得取模

Ⅳ、分析問題

先把幾個概念弄明白：

sz[u] 子樹u的大小，包括u本身
dep[u] 結點u的深度，根節點深度為1
重兒子 節點u的子樹中，sz最大的那個子樹的根，用son[u]表示(葉結點無重兒子)
重鏈 由連接結點與其重兒子的邊連接而成的路徑(單獨的結點也是一條重鏈)
輕鏈 又叫輕邊，樹中除了重鏈剩下的邊
top[u] 結點u所在重鏈dep最小的結點(也就是最上面的點)

原諒我語文不好。。。
放張圖吧QAQ

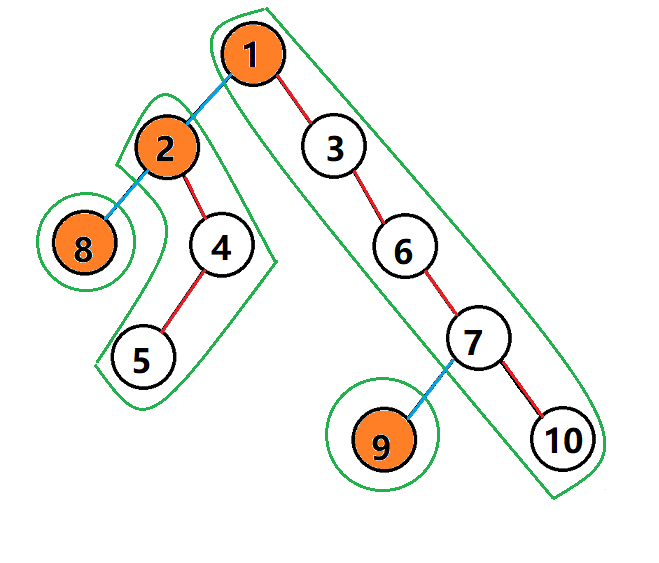
畫的真帥
如圖綠色框起來的是重鏈，橙色的是top，紅的邊是重鏈裏的邊，藍的是輕邊，可以發現輕邊連接兩條重鏈
舉個栗子：
top[8]=8;top[7]=1;top[5]=2;son[1]=2;son[2]=8;son[6]=7;sz[2]=4;

淺談樹鏈剖分