演算法簡介

SOM網路是一種競爭學習型的無監督神經網路，將高維空間中相似的樣本點對映到網路輸出層中的鄰近神經元。

訓練過程簡述：在接收到訓練樣本後，每個輸出層神經元會計算該樣本與自身攜帶的權向量之間的距離，距離最近的神經元成為競爭獲勝者，稱為最佳匹配單元。然後最佳匹配單元及其鄰近的神經元的權向量將被調整，以使得這些權向量與當前輸入樣本的距離縮小。這個過程不斷迭代，直至收斂。

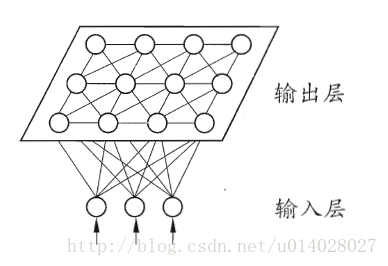
網路結構：輸入層和輸出層（或競爭層），如下圖所示。
輸入層：假設一個輸入樣本為X=[x1,x2,x3,…,xn]，是一個n維向量，則輸入層神經元個數為n個。
輸出層（競爭層）：通常輸出層的神經元以矩陣方式排列在二維空間中，每個神經元都有一個權值向量。
假設輸出層有m個神經元，則有m個權值向量，Wi = [wi1,wi2,....,win], 1<=i<=m。
 

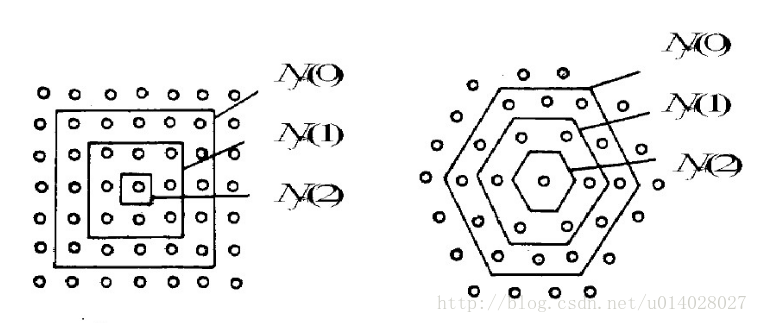
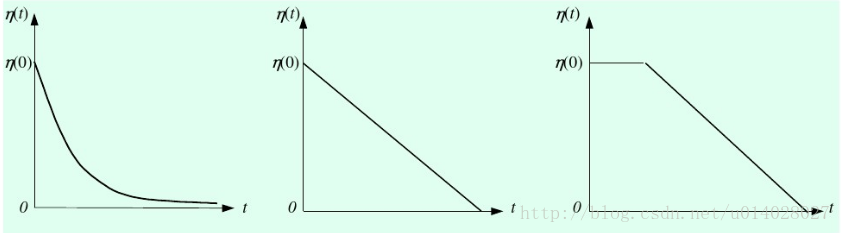
演算法流程：
1. 初始化:權值使用較小的隨機值進行初始化，並對輸入向量和權值做歸一化處理 
          X’ = X/||X|| 
          ω’i= ωi/||ωi||， 1<=i<=m 
          ||X||和||ωi||分別為輸入的樣本向量和權值向量的歐幾里得範數。
2.將樣本輸入網路:樣本與權值向量做點積，點積值最大的輸出神經元贏得競爭，
（或者計算樣本與權值向量的歐幾里得距離，距離最小的神經元贏得競爭）記為獲勝神經元。
3.更新權值:對獲勝的神經元拓撲鄰域內的神經元進行更新,並對學習後的權值重新歸一化。 
        ω(t+1)= ω(t)+ η(t，n) * (x-ω(t))
        η(t，n):η為學習率是關於訓練時間t和與獲勝神經元的拓撲距離n的函式。
        η(t，n)=η(t)e^(-n)
        η(t)的幾種函式影象如下圖所示。

4.更新學習速率η及拓撲鄰域N,N隨時間增大距離變小，如下圖所示。
5.判斷是否收斂。如果學習率η<=ηmin或達到預設的迭代次數，結束演算法。
 

python程式碼實現SOM

import numpy as np
import pylab as pl

class SOM(object):
    def __init__(self, X, output, iteration, batch_size):
        """
        :param X:  形狀是N*D， 輸入樣本有N個,每個D維
        :param output: (n,m)一個元組，為輸出層的形狀是一個n*m的二維矩陣
        :param iteration:迭代次數
        :param batch_size:每次迭代時的樣本數量
        初始化一個權值矩陣，形狀為D*(n*m)，即有n*m權值向量，每個D維
        """
 

        self.X = X
        self.output = output
        self.iteration = iteration
        self.batch_size = batch_size
        self.W = np.random.rand(X.shape[1], output[0] * output[1])
        print (self.W.shape)

    def GetN(self, t):
        """
        :param t:時間t, 這裡用迭代次數來表示時間
        :return: 返回一個整數，表示拓撲距離，時間越大，拓撲鄰域越小
        """
        a = min(self.output)
        return int(a-float(a)*t/self.iteration)

    def Geteta(self, t, n):
        """
        :param t: 時間t, 這裡用迭代次數來表示時間
        :param n: 拓撲距離
        :return: 返回學習率，
        """
        return np.power(np.e, -n)/(t+2)

    def updata_W(self, X, t, winner):
        N = self.GetN(t)
        for x, i in enumerate(winner):
            to_update = self.getneighbor(i[0], N)
            for j in range(N+1):
                e = self.Geteta(t, j)
                for w in to_update[j]:
                    self.W[:, w] = np.add(self.W[:,w], e*(X[x,:] - self.W[:,w]))

    def getneighbor(self, index, N):
        """
        :param index:獲勝神經元的下標
        :param N: 鄰域半徑
        :return ans: 返回一個集合列表，分別是不同鄰域半徑內需要更新的神經元座標
        """
        a, b = self.output
        length = a*b
        def distence(index1, index2):
            i1_a, i1_b = index1 // a, index1 % b
            i2_a, i2_b = index2 // a, index2 % b
            return np.abs(i1_a - i2_a), np.abs(i1_b - i2_b)

        ans = [set() for i in range(N+1)]
        for i in range(length):
            dist_a, dist_b = distence(i, index)
            if dist_a <= N and dist_b <= N: ans[max(dist_a, dist_b)].add(i)
        return ans




    def train(self):
        """
        train_Y:訓練樣本與形狀為batch_size*(n*m)
        winner:一個一維向量，batch_size個獲勝神經元的下標
        :return:返回值是調整後的W
        """
        count = 0
        while self.iteration > count:
            train_X = self.X[np.random.choice(self.X.shape[0], self.batch_size)]
            normal_W(self.W)
            normal_X(train_X)
            train_Y = train_X.dot(self.W)
            winner = np.argmax(train_Y, axis=1).tolist()
            self.updata_W(train_X, count, winner)
            count += 1
        return self.W

    def train_result(self):
        normal_X(self.X)
        train_Y = self.X.dot(self.W)
        winner = np.argmax(train_Y, axis=1).tolist()
        print (winner)
        return winner

def normal_X(X):
    """
    :param X:二維矩陣，N*D，N個D維的資料
    :return: 將X歸一化的結果
    """
    N, D = X.shape
    for i in range(N):
        temp = np.sum(np.multiply(X[i], X[i]))
        X[i] /= np.sqrt(temp)
    return X
def normal_W(W):
    """
    :param W:二維矩陣，D*(n*m)，D個n*m維的資料
    :return: 將W歸一化的結果
    """
    for i in range(W.shape[1]):
        temp = np.sum(np.multiply(W[:,i], W[:,i]))
        W[:, i] /= np.sqrt(temp)
    return W

#畫圖
def draw(C):
    colValue = ['r', 'y', 'g', 'b', 'c', 'k', 'm']
    for i in range(len(C)):
        coo_X = []    #x座標列表
        coo_Y = []    #y座標列表
        for j in range(len(C[i])):
            coo_X.append(C[i][j][0])
            coo_Y.append(C[i][j][1])
        pl.scatter(coo_X, coo_Y, marker='x', color=colValue[i%len(colValue)], label=i)

    pl.legend(loc='upper right')
    pl.show()

#資料集：每三個是一組分別是西瓜的編號，密度，含糖量
data = """
1,0.697,0.46,2,0.774,0.376,3,0.634,0.264,4,0.608,0.318,5,0.556,0.215,
6,0.403,0.237,7,0.481,0.149,8,0.437,0.211,9,0.666,0.091,10,0.243,0.267,
11,0.245,0.057,12,0.343,0.099,13,0.639,0.161,14,0.657,0.198,15,0.36,0.37,
16,0.593,0.042,17,0.719,0.103,18,0.359,0.188,19,0.339,0.241,20,0.282,0.257,
21,0.748,0.232,22,0.714,0.346,23,0.483,0.312,24,0.478,0.437,25,0.525,0.369,
26,0.751,0.489,27,0.532,0.472,28,0.473,0.376,29,0.725,0.445,30,0.446,0.459"""

a = data.split(',')
dataset = np.mat([[float(a[i]), float(a[i+1])] for i in range(1, len(a)-1, 3)])
dataset_old = dataset.copy()

som = SOM(dataset, (5, 5), 1, 30)
som.train()
res = som.train_result()
classify = {}
for i, win in enumerate(res):
    if not classify.get(win[0]):
        classify.setdefault(win[0], [i])
    else:
        classify[win[0]].append(i)
C = []#未歸一化的資料分類結果
D = []#歸一化的資料分類結果
for i in classify.values():
    C.append(dataset_old[i].tolist())
    D.append(dataset[i].tolist())
draw(C)
draw(D)

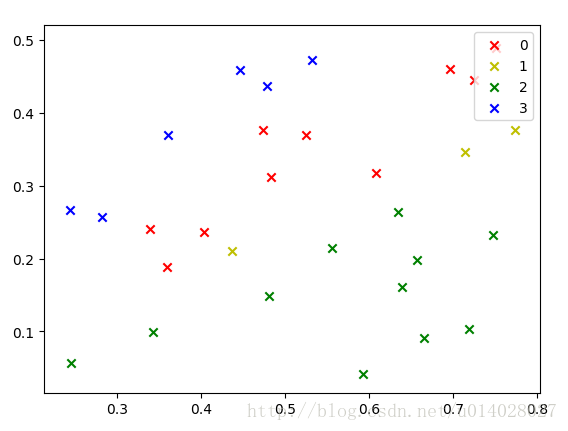
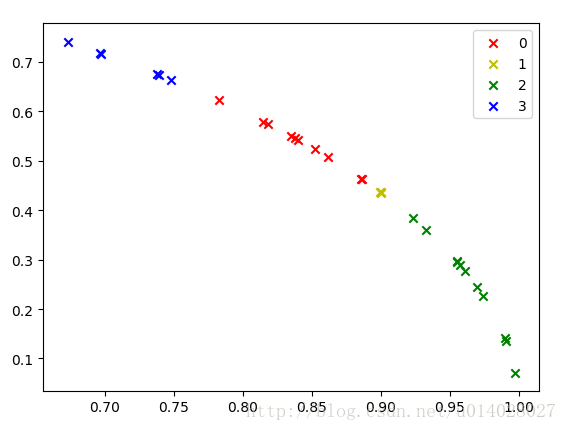
由於資料比較少，就直接用的訓練集做測試了，執行結果圖如下，分別是對未歸一化的資料和歸一化的資料進行的展示。