【0】README

0.1）為什麼有這篇文章？因為 Dijkstra演算法的優先佇列實現 涉及到了一種新的資料結構，即優先佇列（二叉堆）的操作需要更改以適應這種新的資料結構，我們暫且吧它定義為Distance， 而不是單純的int型別；

【1】因為 Dijkstra演算法的優先佇列實現， 需要用到二叉堆的相關操作，但是操作的元素型別（ElementType 不是 單純的int型別）， 而是如下：

struct Distance
{
 int vertexIndex; //當前頂點下標
 int distance; //初始頂點到當前頂點的distance
};

【2】看個荔枝

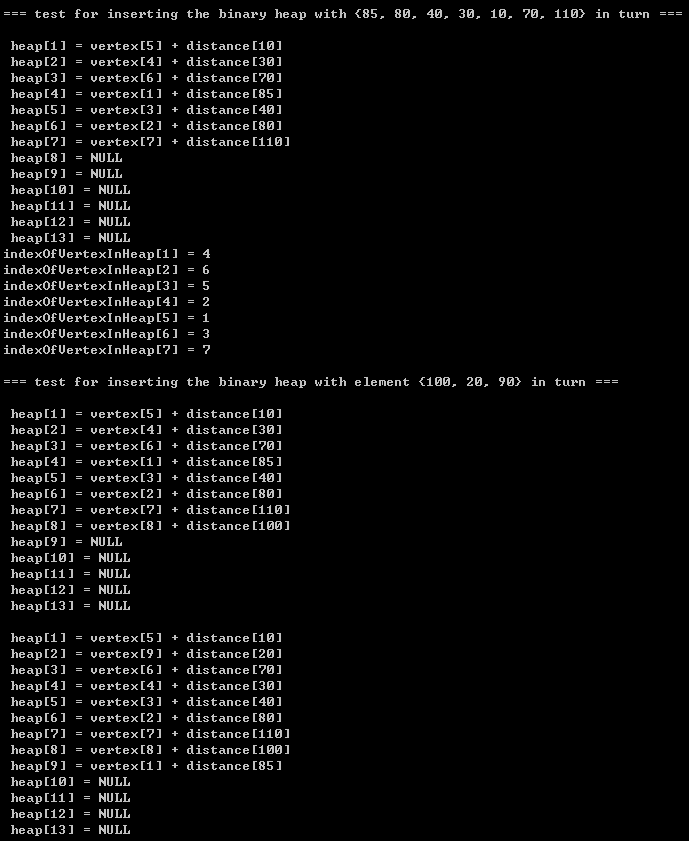
2.1）需要特別說明的是： indexOfVertexInHeap 陣列記錄的是頂點vertex在 heap中的位置， 如 indexOfVertexInHeap [1] = 4；表明heap的第4個位置記錄這 編號為1的vertex;
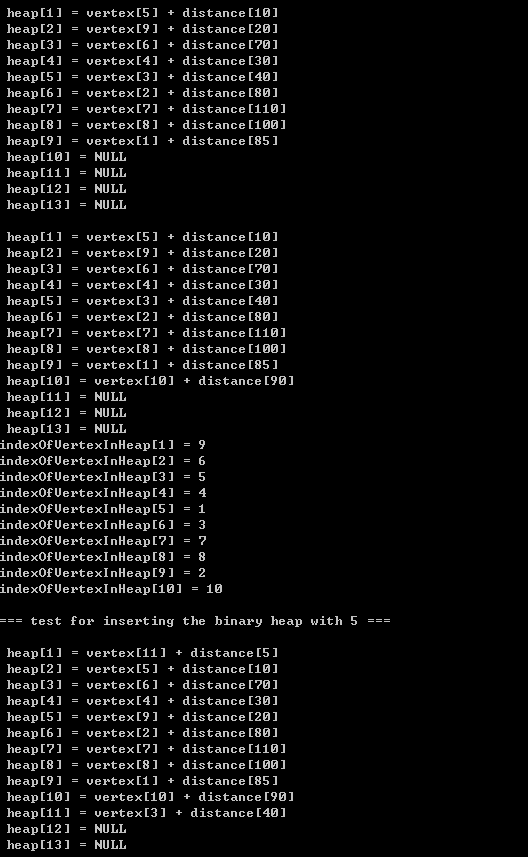
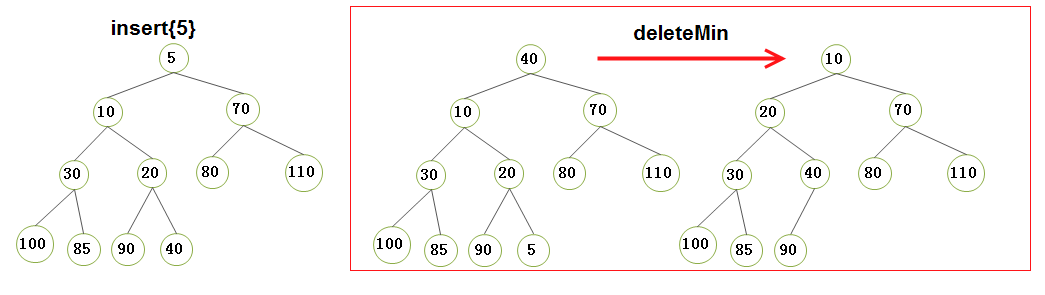
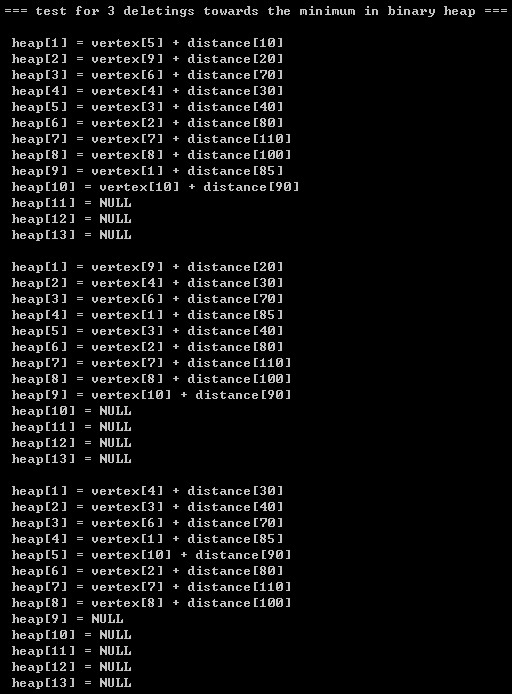
2.2）優先佇列的insert和deleteMin 的執行演示（請將我的手動演示結果同我的程式碼列印結果做對比，經過對比，你發現它們的效果是一致的，恰好說明了我的程式碼的可行性）：

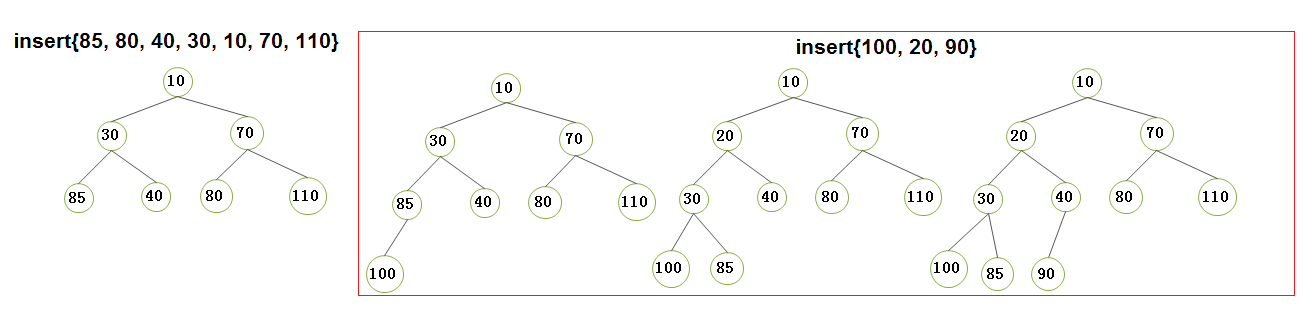
Attention）

• A1）其實本文中的二叉堆優先佇列的實現原始碼和 int型別的優先佇列原始碼類似，只不過它們操作的資料型別不一樣罷了，當然， 這隻需要簡單的修改即可；
• A2）列印結果在文末，可以看到，ElementType採用int 和 Distance的列印效果一樣，這正證明了我們採用Distance結構體對原始碼的修改是無誤的，相比於單純的int 型別，只不過Distance又多了一個 頂點下標vertexIndex成員變數而已；

【3】source code + printing results

1st file：distance.h

#include <stdio.h>

#define Error(str) printf("\n error: %s \n",str)   

struct Distance;
typedef struct
 
 Distance *Distance;
struct Distance
{
    int vertexIndex;
    int distance;
};

Distance makeEmptyDistance();

2nd file：distance.c

#include "distance.h"
#include <malloc.h>

// allocate the memory for Distance struct
Distance makeEmptyDistance()
{
    Distance element;

    element = (Distance)malloc(sizeof(struct Distance));
    if(!element)
    {
        Error("out of space ,from func makeEmptyDistance");
        return NULL;
    }       

    return element;
}

3rd file：binaryheap.h

#include <stdio.h>
#include <malloc.h>
#include "distance.h"

#define ElementType Distance

#define Error(str) printf("\n error: %s \n",str)   

struct BinaryHeap;
typedef struct BinaryHeap *BinaryHeap;

void swap(ElementType x, ElementType y);
BinaryHeap initBinaryHeap(int capacity);
void insert(ElementType value, BinaryHeap bh, int*);
ElementType deleteMin(BinaryHeap, int*);
int isFull(BinaryHeap bh);
int isEmpty(BinaryHeap bh);
void percolateUp(int index, BinaryHeap bh);
void percolateDownFromOne(int index, BinaryHeap bh, int*);
void printBinaryHeap(BinaryHeap bh);
void printBinaryHeapFromZero(BinaryHeap bh);

struct BinaryHeap 
{
    int capacity;
    int size;   
    ElementType *elements;      
};

4th file：binaryheap.c

#include "binaryheap.h"
#include <math.h>

#define MaxInt (int)pow(2, 16)
//judge whether the BinaryHeap is full or not , also 1 or 0 
int isFull(BinaryHeap bh)
{
    return bh->size == bh->capacity - 1; 
}

//judge whether the BinaryHeap is empty or not , also 1 or 0 
int isEmpty(BinaryHeap bh)
{
    return bh->size == 0;
}

// get the left child of node under index with startup 1
int leftChildFromOne(int index)
{
    return index * 2;
}

void printBinaryHeap(BinaryHeap bh)
{
    int i;
    ElementType *temp;

    if(!bh)
        Error("printing execution failure, for binary heap is null, from func printBinaryHeap");    

    temp = bh->elements;
    for(i = 1; i < bh->capacity; i++)
    {
        printf("\n\t heap[%d] = ", i);
        if(i <= bh->size)
            printf("vertex[%d] + distance[%d]", bh->elements[i]->vertexIndex+1, bh->elements[i]->distance);     
        else
            printf("NULL");
    }
    printf("\n");   
}  

//print the binary heap who starts from index 0
void printBinaryHeapFromZero(BinaryHeap bh)
{
    int i;
    ElementType *temp;

    if(!bh)
        Error("printing execution failure, for binary heap is null, from func printBinaryHeap");    

    temp = bh->elements;
    for(i = 0; i < bh->capacity; i++)
    {
        printf("\n\t index[%d] = ", i);
        if(i < bh->size)
            printf("%d", bh->elements[i]->distance);
        else
            printf("NULL");
    }
    printf("\n");
}  

void swap(ElementType x, ElementType y)
{
    struct Distance temp;

    temp = *x;
    *x = *y;
    *y = temp;  
}

ElementType deleteMin(BinaryHeap bh, int* heapIndexRecord)
{   
    ElementType minimum;
    ElementType *data;  

    if(isEmpty(bh))
    {
        Error("failed deleting minimum , for the BinaryHeap is empty, from func deleteMin !");
        return NULL;    
    }

    data = bh->elements;     
    minimum = data[1];

    swap(data[1], data[bh->size]);      
    bh->size-- ; // size-- occurs prior to percolateDownFromOne 
    percolateDownFromOne(1, bh, heapIndexRecord) ;  
    return minimum;
} 

// percolating down the element when its value is greater than children (minimal heap)
 //Attention: all of bh->elements starts from index 1
 void percolateDownFromOne(int index, BinaryHeap bh, int* heapIndexRecord)
 {  
    ElementType *data;
    int size;
    struct Distance temp;
    int child;

    data = bh->elements;
    size = bh->size;    

    for(temp = *data[index]; leftChildFromOne(index) <= size; index = child)
    {
        child = leftChildFromOne(index);
        if(child < size && data[child]->distance > data[child+1]->distance)
            child++;
        if(temp.distance > data[child]->distance)
        {           
            *data[index] = *data[child];            
            heapIndexRecord[bh->elements[index]->vertexIndex] = index; //update the heapIndexRecord
        }
        else
            break;
    }   
    *data[index] = temp;    
    heapIndexRecord[bh->elements[index]->vertexIndex] = index; //update the heapIndexRecord
 }

// Attention, the index of the heap starts from 1
// return the index the element inserted into the binary heap
void insert(ElementType value, BinaryHeap bh, int* heapIndexRecord)
{
    int i;

    if(isFull(bh))
    {
        Error("failed insertion , for the BinaryHeap is full, from func insert!");
        return ;    
    }   
    if(!isEmpty(bh))
        for(i = ++bh->size; bh->elements[i/2]->distance > value->distance; i /= 2)                  
        {
            //copyElement(bh->elements[i/2], bh->elements[i]);       
            *bh->elements[i] = *bh->elements[i/2];
            heapIndexRecord[bh->elements[i]->vertexIndex] = i; //update the heapIndexRecord
        }
    else
        i = ++bh->size;     
    *bh->elements[i] = *value;
    heapIndexRecord[bh->elements[i]->vertexIndex] = i; //update the heapIndexRecord
}

BinaryHeap initBinaryHeap(int capacity)
{
    BinaryHeap bh;
    ElementType *temp;
    int i;

    bh = (BinaryHeap)malloc(sizeof(struct BinaryHeap));
    if(!bh) {
        Error("out of space, from func initBinaryHeap");        
        return NULL;
    }  
    bh->capacity = capacity;
    bh->size = 0;

    temp = (ElementType*)malloc(capacity * sizeof(Distance));
    if(!temp) {
        Error("out of space, from func initBinaryHeap");        
        return NULL;
    } 
    bh->elements = temp;

    for(i=0; i < capacity; i++)
    {
        temp[i] = (ElementType)malloc(sizeof(struct Distance));
        if(!temp[i]) {
            Error("out of space, from func initBinaryHeap");        
            return NULL;
        }       
    }

    return bh;
}

// allocate the memory for storing index of  vertex in heap and let every element -1
int *makeEmptyArray(int size)
{
    int *array;
    int i;

    array = (int*)malloc(size * sizeof(int));
    if(!array)
    {
        Error("out of space ,from func makeEmptyArray");
        return NULL;
    }       
    for(i=0; i<size; i++)
        array[i] = -1;

    return array;
} 


void printIndexOfVertexInHeap(int size, int *array)
{
    int i;

    for(i=0; i<size; i++)    
        printf("\tindexOfVertexInHeap[%d] = %d\n", i+1, array[i]);   
}

int main()
{
    int data[] = {85, 80, 40, 30, 10, 70, 110}; // P141 
    int buildHeapData[] = {150, 80, 40, 30, 10, 70, 110, 100, 20, 90, 60, 50, 120, 140, 130};
    BinaryHeap bh;  
    int size;
    int i;  
    int capacity;
    Distance tempDisStruct;
    int *indexOfVertexInHeap;

    printf("\n\t=== test for inserting the binary heap with {85, 80, 40, 30, 10, 70, 110} in turn ===\n");
    capacity = 14;
    bh = initBinaryHeap(capacity);
    size = 7;   

    tempDisStruct = makeEmptyDistance(); 
    indexOfVertexInHeap = makeEmptyArray(size);

    for(i = 0; i < size; i++) 
    {
        tempDisStruct->distance = data[i];
        tempDisStruct->vertexIndex = i;
        insert(tempDisStruct, bh, indexOfVertexInHeap);
    }   
    printBinaryHeap(bh);
    printIndexOfVertexInHeap(bh->size, indexOfVertexInHeap);

    printf("\n\t=== test for inserting the binary heap with element {100, 20, 90} in turn ===\n");

    tempDisStruct->distance = 100;
    tempDisStruct->vertexIndex = size;
    insert(tempDisStruct, bh, indexOfVertexInHeap); 
    printBinaryHeap(bh);

    tempDisStruct->distance = 20;
    tempDisStruct->vertexIndex = size+1;
    insert(tempDisStruct, bh, indexOfVertexInHeap); 
    printBinaryHeap(bh);

    tempDisStruct->distance = 90;
    tempDisStruct->vertexIndex = size+2;
    insert(tempDisStruct, bh, indexOfVertexInHeap); 
    printBinaryHeap(bh);

    printIndexOfVertexInHeap(bh->size, indexOfVertexInHeap);

    printf("\n\t=== test for inserting the binary heap with 5 ===\n");  
    tempDisStruct->distance = 5;
    tempDisStruct->vertexIndex = size+3;
    insert(tempDisStruct, bh, indexOfVertexInHeap); 
    printBinaryHeap(bh);

    printf("\n\t=== test for 3 deletings towards the minimum in binary heap ===\n");
    deleteMin(bh, indexOfVertexInHeap); 
    printBinaryHeap(bh);
    deleteMin(bh, indexOfVertexInHeap);     
    printBinaryHeap(bh);
    deleteMin(bh, indexOfVertexInHeap); 
    printBinaryHeap(bh);
}

3.3）printing results：