部分理解： 關於決策樹生成 決策樹的生成過程就是 使用滿足劃分準則的特徵不斷的將資料集劃分為純度更高，不確定性更小的子集的過程。 對於當前資料集D的每一次的劃分，都希望根據某特徵劃分之後的各個子集的純度更高，不確定性更小。 而如何度量劃分資料集前後的資料集的純度以及不確定性呢？     答案：特徵選擇準則，比如：資訊增益，資訊增益率，基尼指數 特徵選擇準則： 目的：使用某特徵對資料集劃分之後，各資料子集的純度要比劃分前的資料集D的純度高（不確定性要比劃分前資料集D的不確定性低。） 注意：          1. 劃分後的純度為各資料子集的純度的加和（子集佔比*子集的經驗熵）。          2. 度量劃分前後的純度變化 用子集的純度之和與劃分前的資料集D的純度 進行對比。 特徵選擇的準則就是 度量樣本集合不確定性以及純度的方法。本質相同，定義不同而已。

特徵選擇的準則主要有以下三種：資訊增益，資訊增益率，基尼指數 首先介紹一下熵的概念以及理解： 熵：度量隨機變數的不確定性。（純度） 定義：假設隨機變數X的可能取值有x_1，x₂， ... , x_n          對於每一個可能的取值x_i，其概率 P(X=x_i) = p_i , ( i = 1,2, ... , n)          因此隨機變數X的熵：                                  

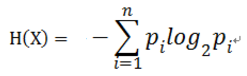
對於樣本集合D來說，隨機變數X是樣本的類別，即，假設樣本有k個類別，每個類別的概率是，其中|C_k|表示類別k的樣本個數，|D|表示樣本總數

則對於樣本集合D來說熵（經驗熵）

為：

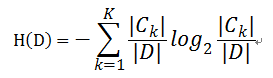
• 資訊增益（ ID3演算法 ）

      定義： 以某特徵劃分資料集前後的熵的差值

      在熵的理解那部分提到了，熵可以表示樣本集合的不確定性，熵越大，樣本的不確定性就越大。因此可以使用劃分前後集合熵的差值來衡量使用當前特徵對於樣本集合D劃分效果的好壞。

      劃分前樣本集合D的熵是一定的 ，entroy(前)，       使用某個特徵A劃分資料集D，計算劃分後的資料子集的熵 entroy(後)                                    資訊增益 =  entroy(前) -  entroy(後)           書中公式: 做法：計算使用所有特徵劃分資料集D，得到多個特徵劃分資料集D的資訊增益，從這些資訊增益中選擇最大的，因而當前結點的劃分特徵便是使資訊增益最大的劃分所使用的特徵。 資訊增益的理解： 對於待劃分的資料集D，其 entroy(前)是一定的，但是劃分之後的熵 entroy(後)是不定的，entroy(後)越小說明使用此特徵劃分得到的子集的不確定性越小（也就是純度越高），因此 entroy(前) -  entroy(後)差異越大，說明使用當前特徵劃分資料集D的話，其純度上升的更快。而我們在構建最優的決策樹的時候總希望能更快速到達純度更高的集合，這一點可以參考優化演算法中的梯度下降演算法，每一步沿著負梯度方法最小化損失函式的原因就是負梯度方向是函式值減小最快的方向。同理：在決策樹構建的過程中我們總是希望集合往最快到達純度更高的子集合方向發展，因此我們總是選擇使得資訊增益最大的特徵來劃分當前資料集D。  缺點：資訊增益偏向取值較多的特徵        原因：當特徵的取值較多時，根據此特徵劃分更容易得到純度更高的子集，因此劃分之後的熵更低，由於劃分前的熵是一定的，因此資訊增益更大，因此資訊增益比較 偏向取值較多的特徵。

•  解決方法 :  資訊增益比（ C4.5演算法 ）

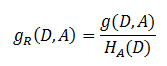      資訊增益比 = 懲罰引數 * 資訊增益 書中公式：        注意：其中的H_A(D)，對於樣本集合D，將當前特徵A作為隨機變數（取值是特徵A的各個特徵值），求得的經驗熵。       （之前是把集合類別作為隨機變數，現在把某個特徵作為隨機變數，按照此特徵的特徵取值對集合D進行劃分，計算熵H_A(D)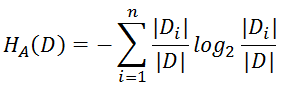）       資訊增益比本質： 是在資訊增益的基礎之上乘上一個懲罰引數。特徵個數較多時，懲罰引數較小；特徵個數較少時，懲罰引數較大。         懲罰引數：資料集D以特徵A作為隨機變數的熵的倒數，即：將特徵A取值相同的樣本劃分到同一個子集中（之前所說資料集的熵是依據類別進行劃分的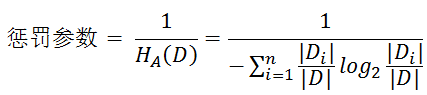）                  缺點：資訊增益比偏向取值較少的特徵            原因：  當特徵取值較少時H_A(D)的值較小，因此其倒數較大，因而資訊增益比較大。因而偏向取值較少的特徵。         使用資訊增益比：基於以上缺點，並不是直接選擇資訊增益率最大的特徵，而是現在候選特徵中找出資訊增益高於平均水平的特徵，然後在這些特徵中再選擇資訊增益率最高的特徵。   

• 基尼指數（ CART演算法 ---分類樹）

定義：基尼指數（基尼不純度）：表示在樣本集合中一個隨機選中的樣本被分錯的概率。

        注意： Gini指數越小表示集合中被選中的樣本被分錯的概率越小，也就是說集合的純度越高，反之，集合越不純。

即 基尼指數（基尼不純度）= 樣本被選中的概率 * 樣本被分錯的概率

書中公式：

    

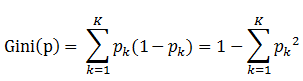
說明:

1. p_k表示選中的樣本屬於k類別的概率，則這個樣本被分錯的概率是(1-p_k)

2. 樣本集合中有K個類別，一個隨機選中的樣本可以屬於這k個類別中的任意一個，因而對類別就加和

3. 當為二分類是，Gini(P) = 2p(1-p)

樣本集合D的Gini指數 ： 假設集合中有K個類別，則：

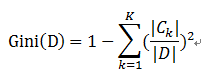
基於特徵A劃分樣本集合D之後的基尼指數：

需要說明的是CART是個二叉樹，也就是當使用某個特徵劃分樣本集合只有兩個集合：1. 等於給定的特徵值 的樣本集合D₁ ， 2 不等於給定的特徵值 的樣本集合D₂

實際上是對擁有多個取值的特徵的二值處理。

舉個例子：

    假設現在有特徵 “學歷”，此特徵有三個特徵取值： “本科”，“碩士”， “博士”，

    當使用“學歷”這個特徵對樣本集合D進行劃分時，劃分值分別有三個，因而有三種劃分的可能集合，劃分後的子集如下：

1. 1.     劃分點： “本科”，劃分後的子集合 ： {本科}，{碩士，博士}
   2.     劃分點： “碩士”，劃分後的子集合 ： {碩士}，{本科，博士}
   3. 劃分點： “碩士”，劃分後的子集合 ： {博士}，{本科，碩士}

          對於上述的每一種劃分，都可以計算出基於 劃分特徵= 某個特徵值 將樣本集合D劃分為兩個子集的純度：

             

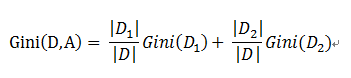
     因而對於一個具有多個取值（超過2個）的特徵，需要計算以每一個取值作為劃分點，對樣本D劃分之後子集的純度Gini(D,A_i)，(其中A_i 表示特徵A的可能取值)

     然後從所有的可能劃分的Gini(D,A_i)中找出Gini指數最小的劃分，這個劃分的劃分點，便是使用特徵A對樣本集合D進行劃分的最佳劃分點。