二叉樹常見演算法總結-基本二叉樹
阿新 • • 發佈:2018-12-31
二叉樹是最經典的資料結構之一,其結構型別和演算法操作也是十分多,今天來做一個總結(今天先不討論對B樹,紅黑樹那種比較高階的資料結構)。
樹結構,一般用節點引用兩個子節點作為左右節點。結構程式碼如下

PS:有些時候也要有個指標指向父節點的,比如劍指offer那裡有個題目是尋找中序遍歷的時候要你尋找給出的節點在中序遍歷的時候下一個節點是什麼,這時候就需要了。
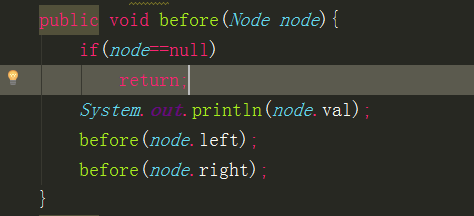
好了,現在先討論一下二叉樹的四種遍歷演算法,先序,中序,後序遍歷,以及層次遍歷。先序遍歷就是先訪問父節點,然後再訪問左子樹和右子樹。中序就是先訪問左子樹,然後訪問父節點,最後訪問右子樹。後序就是先訪問左子樹,和右子樹,最後訪問父節點。很抽象吧。先上程式碼,其實對著程式碼好好想下就很清晰了。


下面我們來看看怎麼實現層次遍歷的,其實層次遍歷是藉助一個佇列去實現的,而劍指offer裡面也很多題目需要我們用到層次遍歷的變形。
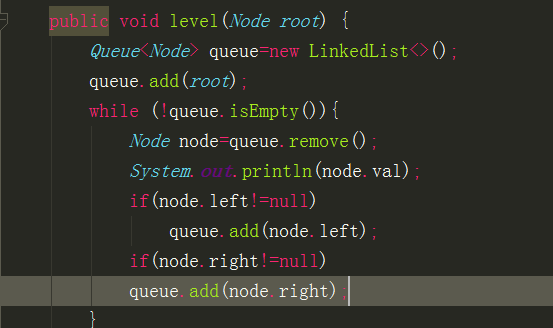
現在我們討論一下他們的演算法複雜度,其實這個也很簡單,因為每個節點都被訪問了一次,所以他的時間複雜度顯而易見是O(n)。(PS:這個我面試YY和網易都被問到了)
然後怎麼求二叉樹的高度呢,這裡也給出他的實現
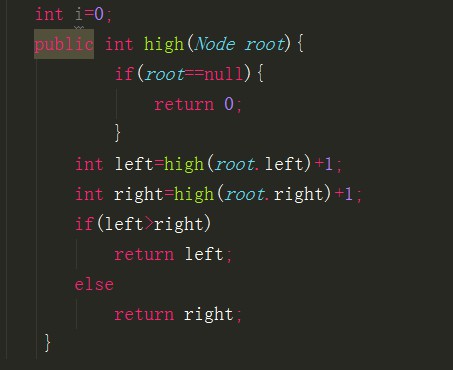
為什麼我們總是討論二叉樹而不討論3,4,5個節點的樹呢,其實很簡單。樹都可以用二叉樹表示的。樹我們一個比較好的表示方法是父節點記錄長子(第一個子節點),然後子節點之間使用引用來進行溝通。如下面程式碼
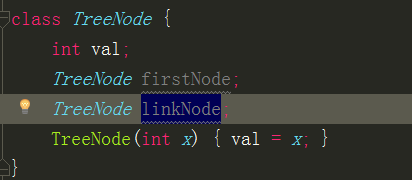
其實敏感的同學也看出來了,樹節點的類結構和二叉樹是完全一樣的,這也就是為什麼樹可以用二叉樹進行表示了
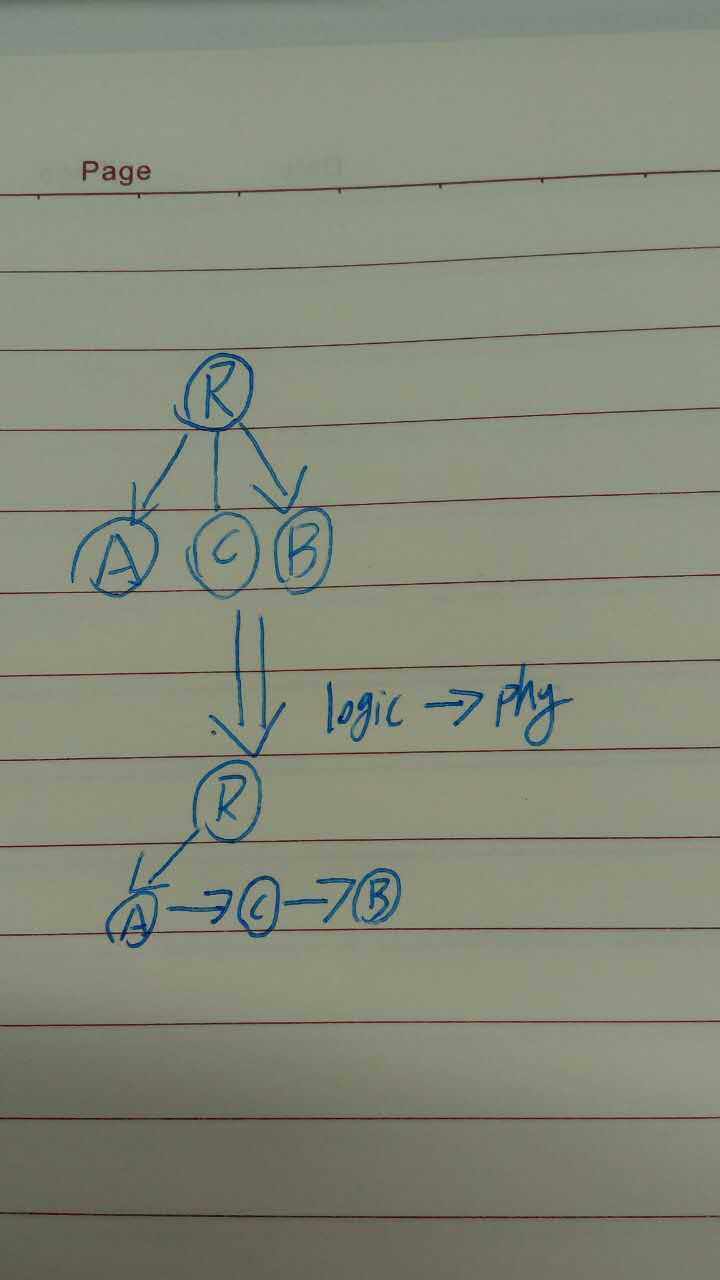
然後我們把父節點到長子的邊作為左邊,兄弟連結串列之間引用作為右邊就可以轉化為
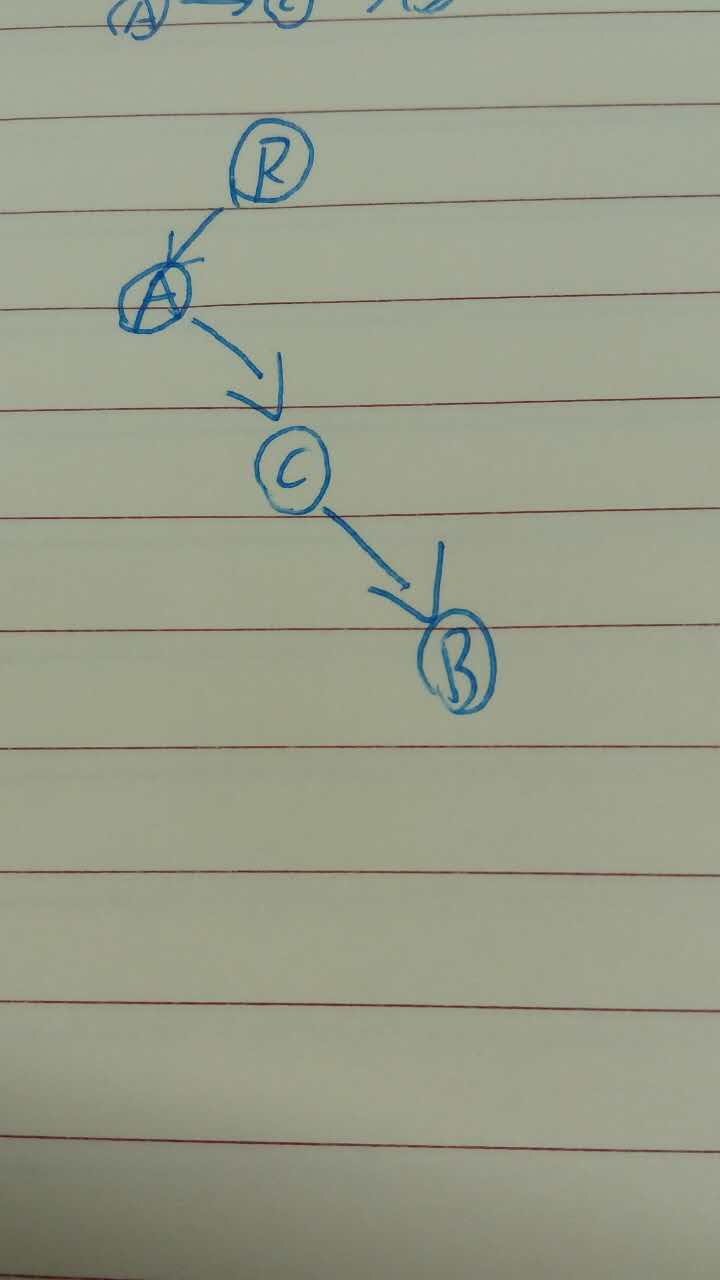
現在我們就很清楚看到為什麼可以把二叉樹來表示各種樹的原因啦!