關於神經網路激勵函式的作用，常聽到的解釋是：不使用激勵函式的話，神經網路的每層都只是做線性變換，多層輸入疊加後也還是線性變換。因為線性模型的表達能力不夠，激勵函式可以引入非線性因素。 其實很多時候我們更想直觀的瞭解激勵函式的是如何引入非線性因素的。

我們使用神經網路來分割平面空間作為例子。

無激勵函式的神經網路

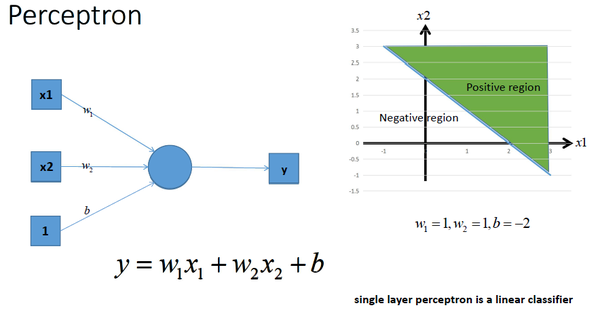
神經網路最簡單的結構就是單輸出的單層感知機，單層感知機只有輸入層和輸出層，分別代表了神經感受器和神經中樞。下圖是一個只有2個輸入單元和1個輸出單元的簡單單層感知機。圖中x1、w2代表神經網路的輸入神經元受到的刺激，w1、w2代表輸入神經元和輸出神經元間連線的緊密程度，b代表輸出神經元的興奮閾值，y為輸出神經元的輸出。我們使用該單層感知機劃出一條線將平面分割開，如圖所示： 

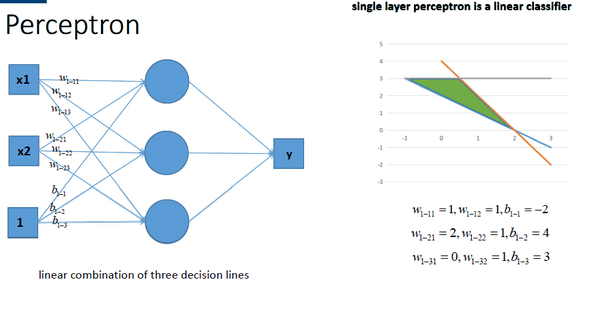
同理，我們也可以將多個感知機（注意，不是多層感知機）進行組合獲得更強的平面分類能力，如圖所示： 

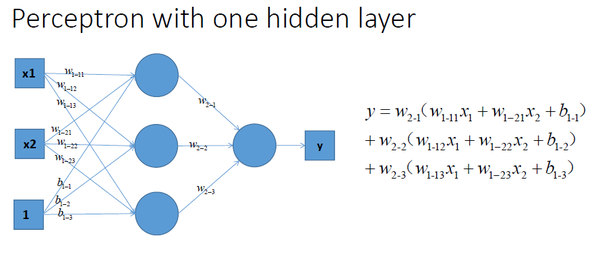
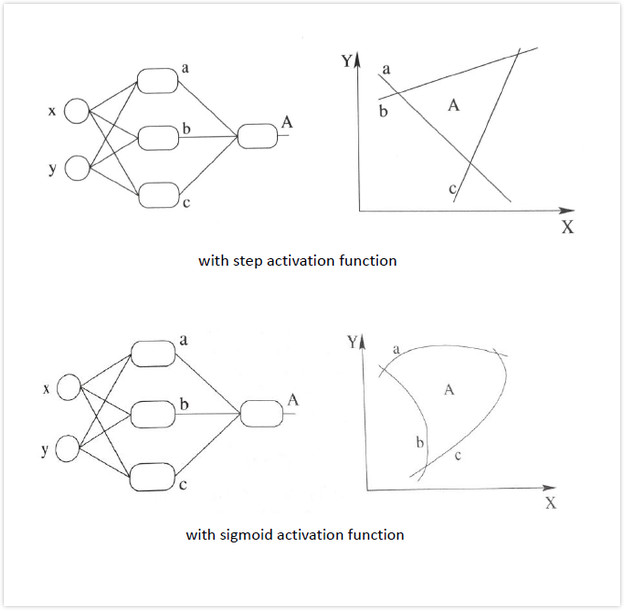
再看看包含一個隱層的多層感知機的情況，如圖所示： 

仔細看的話不難發現，上面三種沒有激勵函式的神經網路的輸出是線性方程，其在用複雜的線性組合來逼近曲線。

有激勵函式的神經網路

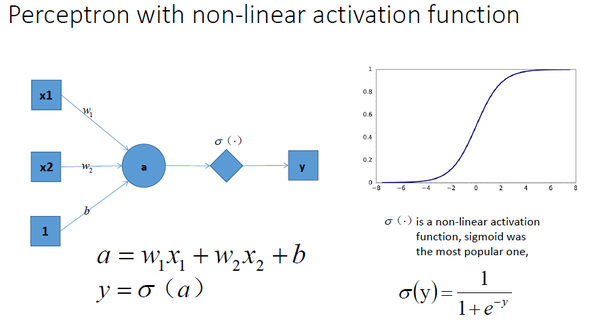
我們在神經網路每一層神經元做完線性變換以後，加上一個非線性激勵函式對線性變換的結果進行轉換，那麼輸出就是一個不折不扣的非線性函數了，如圖所示： 

拓展到多層神經網路的情況, 更剛剛一樣的結構, 加上非線性激勵函式之後, 輸出就變成了一個複雜的非線性函數了，如圖所示： 

加入非線性激勵函式後，神經網路就有可能學習到平滑的曲線來分割平面，而不是用複雜的線性組合逼近平滑曲線來分割平面。 這就是為什麼我們要有非線性的啟用函式的原因。如下圖所示說明加入非線性啟用函式後的差異，上圖為用線性組合逼近平滑曲線來分割平面，下圖為平滑的曲線來分割平面： 

參考資料