拓展kmp演算法總結
拓展kmp是對KMP演算法的擴充套件,它解決如下問題:
定義母串S,和字串T,設S的長度為n,T的長度為m,求T與S的每一個字尾的最長公共字首,也就是說,設extend陣列,extend[i]表示T與S[i,n-1]的最長公共字首,要求出所有extend[i](0<=i<n)。
注意到,如果有一個位置extend[i]=m,則表示T在S中出現,而且是在位置i出現,這就是標準的KMP問題,所以說拓展kmp是對KMP演算法的擴充套件,所以一般將它稱為擴充套件KMP演算法。
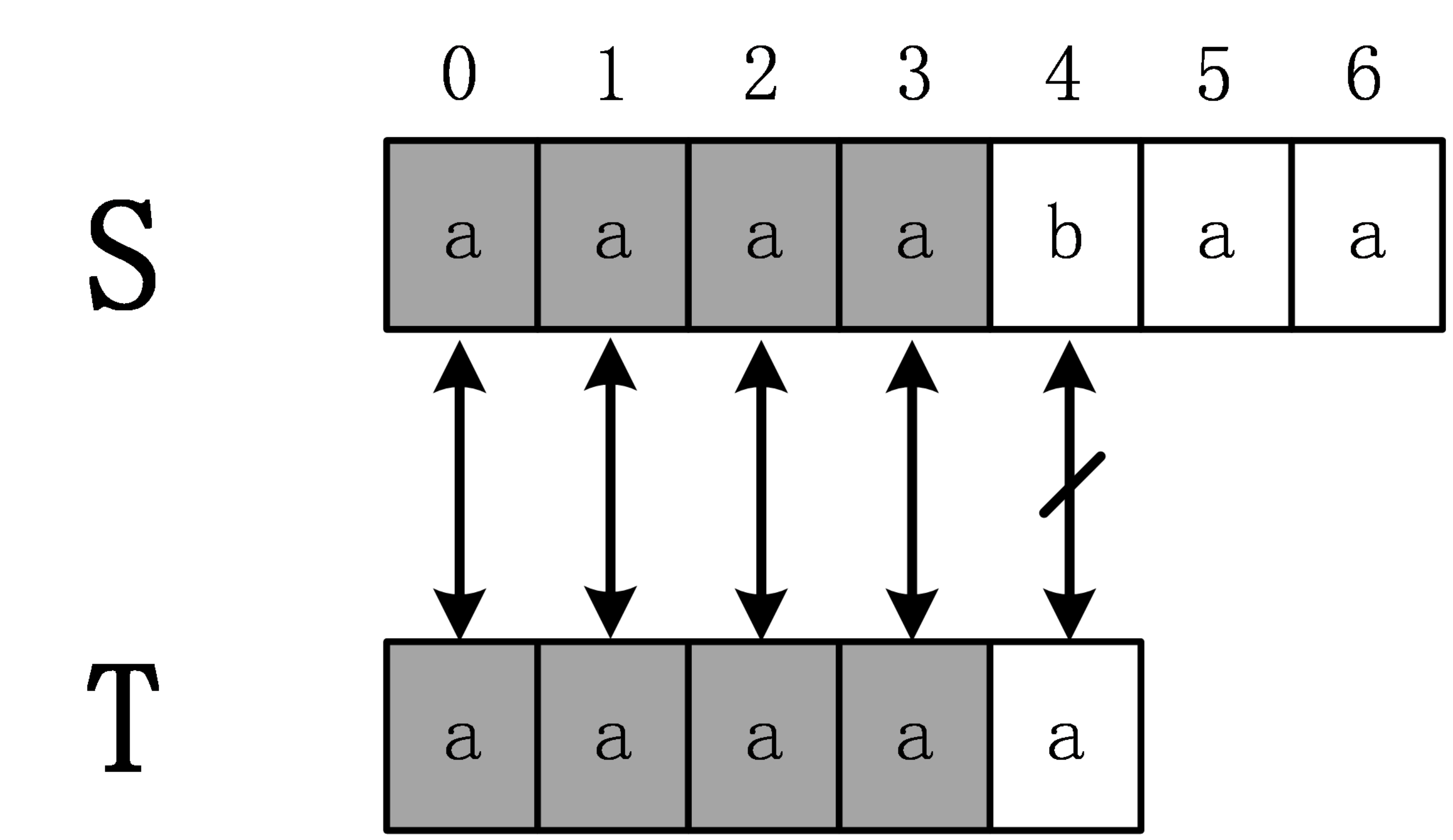
下面舉一個例子,S=”aaaabaa”,T=”aaaaa”,首先,計算extend[0]時,需要進行5次匹配,直到發生失配。
從而得知extend[0]=4,下面計算extend[1],在計算extend[1]時,是否還需要像計算extend[0]時從頭開始匹配呢?答案是否定的,因為通過計算extend[0]=4,從而可以得出S[0,3]=T[0,3],進一步可以得到 S[1,3]=T[1,3],計算extend[1]時,事實上是從S[1]開始匹配,設輔助陣列next[i]表示T[i,m-1]和T的最長公共字首長度。在這個例子中,next[1]=4,即T[0,3]=T[1,4],進一步得到T[1,3]=T[0,2],所以S[1,3]=T[0,2],所以在計算extend[1]時,通過extend[0]的計算,已經知道S[1,3]=T[0,2],所以前面3個字元已經不需要匹配,直接匹配S[4]和T[3]即可,這時一次就發生失配,所以extend[1]=3。這個例子很有代表性,有興趣的讀者可以繼續計算完剩下的extend陣列。
1. 拓展kmp演算法一般步驟
通過上面的例子,事實上已經體現了拓展kmp演算法的思想,下面來描述拓展kmp演算法的一般步驟。
首先我們從左到右依次計算extend陣列,在某一時刻,設extend[0...k]已經計算完畢,並且之前匹配過程中所達到的最遠位置為P,所謂最遠位置,嚴格來說就是i+extend[i]-1的最大值(0<=i<=k),並且設取這個最大值的位置為po,如在上一個例子中,計算extend[1]時,P=3,po=0。
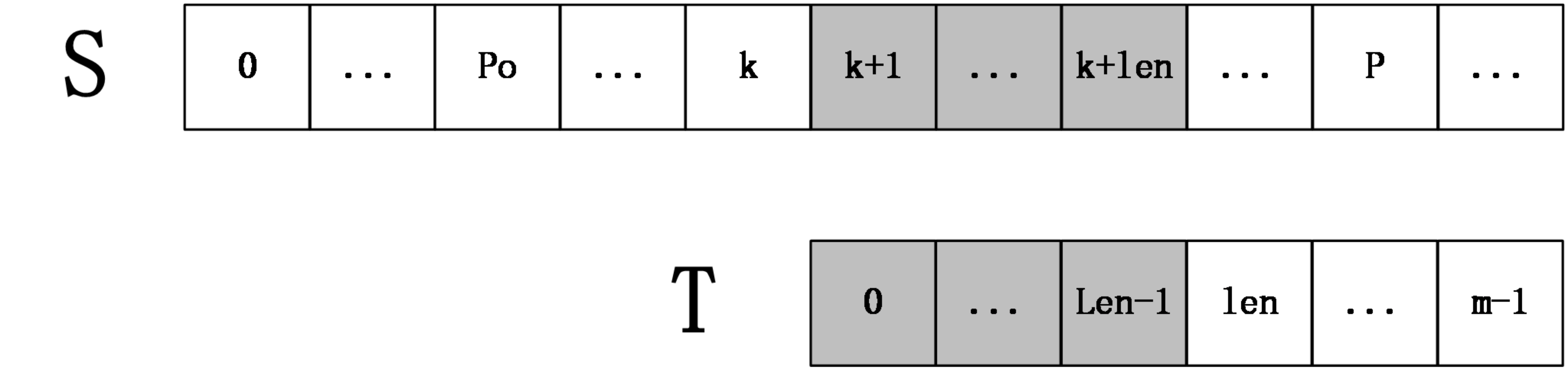
現在要計算extend[k+1],根據extend陣列的定義,可以推斷出S[po,P]=T[0,P-po],從而得到 S[k+1,P]=T[k-po+1,P-po],令len=next[k-po+1],(回憶下next陣列的定義),分兩種情況討論:
第一種情況:k+len<P
如下圖所示:
上圖中,S[k+1,k+len]=T[0,len-1],然後S[k+len+1]一定不等於T[len],因為如果它們相等,則有S[k+1,k+len+1]=T[k+po+1,k+po+len+1]=T[0,len],那麼next[k+po+1]=len+1,這和next陣列的定義不符(next[i]表示T[i,m-1]和T的最長公共字首長度),所以在這種情況下,不用進行任何匹配,就知道extend[k+1]=len。
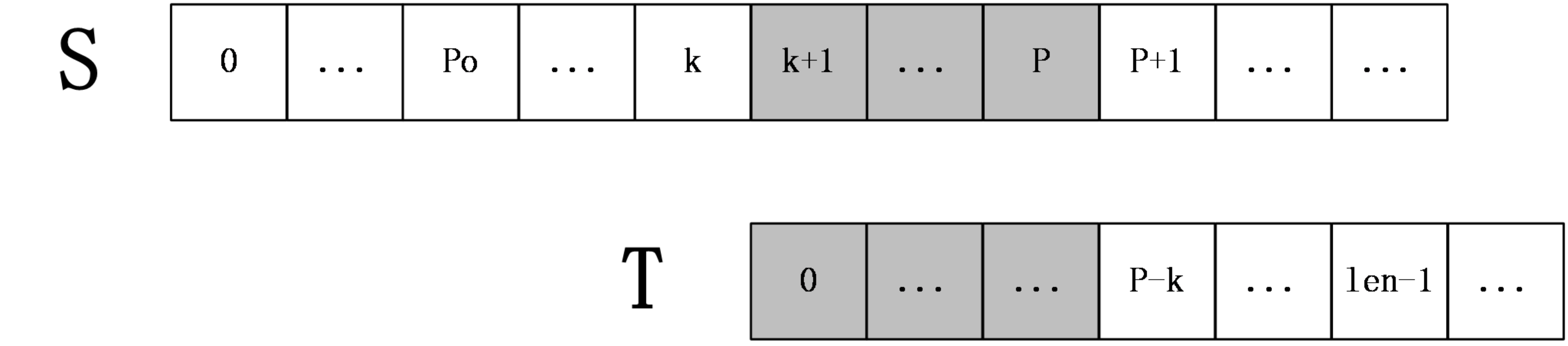
第二種情況: k+len>=P
如下圖:
上圖中,S[p+1]之後的字元都是未知的,也就是還未進行過匹配的字串,所以在這種情況下,就要從S[P+1]和T[P-k+1]開始一一匹配,直到發生失配為止,當匹配完成後,如果得到的extend[k+1]+(k+1)大於P則要更新未知P和po。
至此,拓展kmp演算法的過程已經描述完成,細心地讀者可能會發現,next陣列是如何計算還沒有進行說明,事實上,計算next陣列的過程和計算extend[i]的過程完全一樣,將它看成是以T為母串,T為字串的特殊的拓展kmp演算法匹配就可以了,計算過程中的next陣列全是已經計算過的,所以按照上述介紹的演算法計算next陣列即可,這裡不再贅述。
2. 時間複雜度分析
下面來分析一下演算法的時間複雜度,通過上面的演算法介紹可以知道,對於第一種情況,無需做任何匹配即可計算出extend[i],對於第二種情況,都是從未被匹配的位置開始匹配,匹配過的位置不再匹配,也就是說對於母串的每一個位置,都只匹配了一次,所以演算法總體時間複雜度是O(n)的,同時為了計算輔助陣列next[i]需要先對字串T進行一次拓展kmp演算法處理,所以拓展kmp演算法的總體複雜度為O(n+m)的。其中n為母串的長度,m為子串的長度。
下面是拓展kmp演算法的關鍵部分程式碼實現。
const int maxn=100010; //字串長度最大值
int next[maxn],ex[maxn]; //ex陣列即為extend陣列
//預處理計算next陣列
void GETNEXT(char *str)
{
int i=0,j,po,len=strlen(str);
next[0]=len;//初始化next[0]
while(str[i]==str[i+1]&&i+1<len)//計算next[1]
i++;
next[1]=i;
po=1;//初始化po的位置
for(i=2;i<len;i++)
{
if(next[i-po]+i<next[po]+po)//第一種情況,可以直接得到next[i]的值
next[i]=next[i-po];
else//第二種情況,要繼續匹配才能得到next[i]的值
{
j=next[po]+po-i;
if(j<0)j=0;//如果i>po+next[po],則要從頭開始匹配
while(i+j<len&&str[j]==str[j+i])//計算next[i]
j++;
next[i]=j;
po=i;//更新po的位置
}
}
}
//計算extend陣列
void EXKMP(char *s1,char *s2)
{
int i=0,j,po,len=strlen(s1),l2=strlen(s2);
GETNEXT(s2);//計運算元串的next陣列
while(s1[i]==s2[i]&&i<l2&&i<len)//計算ex[0]
i++;
ex[0]=i;
po=0;//初始化po的位置
for(i=1;i<len;i++)
{
if(next[i-po]+i<ex[po]+po)//第一種情況,直接可以得到ex[i]的值
ex[i]=next[i-po];
else//第二種情況,要繼續匹配才能得到ex[i]的值
{
j=ex[po]+po-i;
if(j<0)j=0;//如果i>ex[po]+po則要從頭開始匹配
while(i+j<len&&j<l2&&s1[j+i]==s2[j])//計算ex[i]
j++;
ex[i]=j;
po=i;//更新po的位置
}
}
}