Algorithm Part I:Union-Find
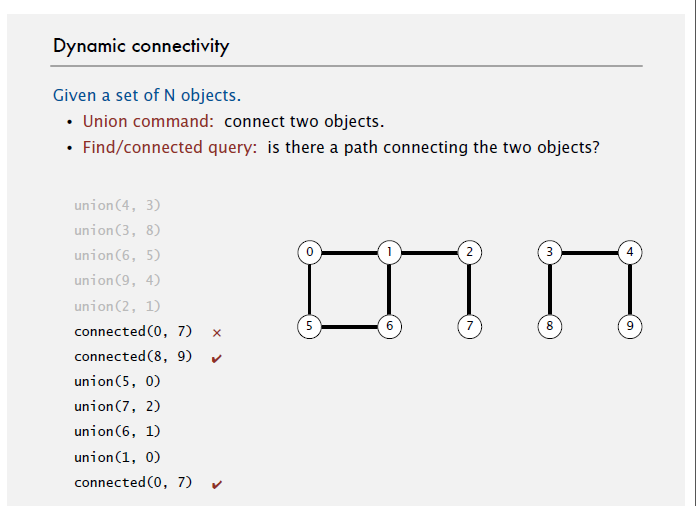
1.動態聯通性問題描述:
有N個元素,開始時我們讓每一個元素肚子構成一個集合。然後按一定的順序將屬於同一組中的元素合併,構成新的集合。其間要反覆查詢某個元素在哪個集合中。如下所示:
解決辦法:
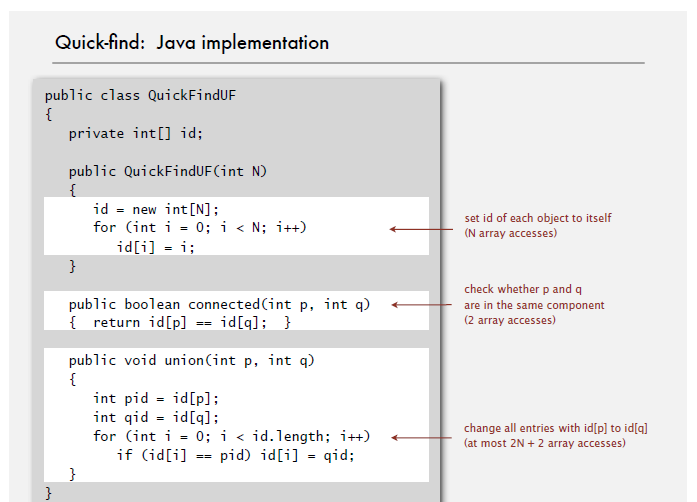
(1)Quick-Find
宣告一個長度為N的陣列id,陣列中元素的值代表它所屬組的編號。將陣列中的元素初始化為每個元素的索引值,這樣就表示開始時每個元素各自構成一個獨立的集合。每次union(i,j)的時候就將所有組編號等於id[i]的元素的組編號變為id[j]。每次查詢元素i的組編號時,返回id[i]即可。
實現:
時間複雜度分析:union操作的時間複雜度為O(n),find操作的時間複雜度為O(1)
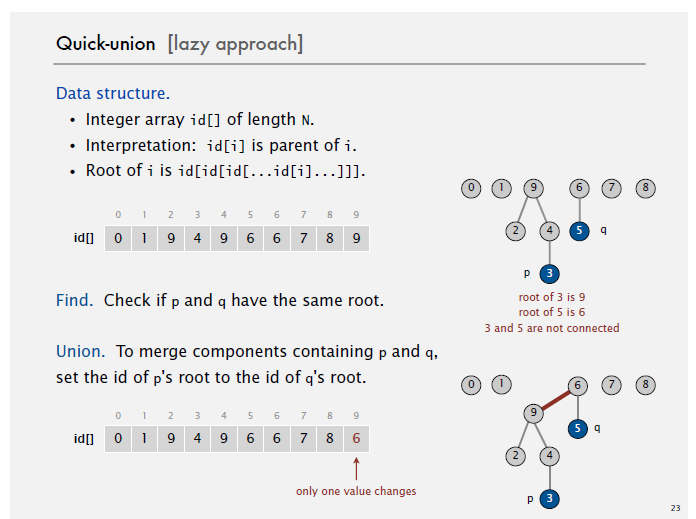
(2)Quick-Union
同樣是宣告一個長度為N的int型陣列id。但與Quick-Find方法不同的是,Quick-Union讓每一個集合中的元素構成一棵樹,每一個元素對應的id存的是自己在樹上的父節點。在執行union(i,j)操作時,將i元素所在樹的根指向j所在元素的根。在查詢元素i的id時,返回元素i所在集合的樹的根節點index即可。
實現:
時間複雜度分析:union操作的時間複雜度為O(n),find的時間複雜度為O(n).
(3)改進的Quick-Union
為了防止構建樹的過程中出現tall trees,我們記錄每個集合的大小。每次union的時候將小集合對應樹的根連結到大集合所對應樹的根上。
實現:
時間複雜度分析:union操作的時間複雜度為lg(n),find操作的時間複雜度為lg(n).
2.Programming Assignments
問題描述:
Programming Assignment 1: Percolation
Write a program to estimate the value of the percolation threshold via Monte Carlo simulation.
Install a Java programming environment. Install a Java programming environment on your computer by following these step-by-step instructions for your operating system [
Percolation. Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations.
The model. We model a percolation system using an N-by-N grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. (For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.)

The problem. In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and therefore blocked with probability 1 − p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for 20-by-20 random grid (left) and 100-by-100 random grid (right).


When N is sufficiently large, there is a threshold value p* such that when p < p* a random N-by-N grid almost never percolates, and when p > p*, a random N-by-N grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p*.
Percolation data type. To model a percolation system, create a data type Percolation with the following API:
public class Percolation {
public Percolation(int N) // create N-by-N grid, with all sites blocked
public void open(int i, int j) // open site (row i, column j) if it is not already
public boolean isOpen(int i, int j) // is site (row i, column j) open?
public boolean isFull(int i, int j) // is site (row i, column j) full?
public boolean percolates() // does the system percolate?
public static void main(String[] args) // test client, optional
}
By convention, the row and column indices i and j are integers between 1 and N, where (1, 1) is the upper-left site: Throw an IndexOutOfBoundsException if any argument to open(), isOpen(), or isFull() is outside its prescribed range. The constructor should throw an IllegalArgumentException if N ≤ 0. The constructor should take time proportional to N2; all methods should take constant time plus a constant number of calls to the union-find methods union(), find(), connected(), and count().
Monte Carlo simulation. To estimate the percolation threshold, consider the following computational experiment:
Initialize all sites to be blocked. Repeat the following until the system percolates: Choose a site (row i, column j) uniformly at random among all blocked sites. Open the site (row i, column j). The fraction of sites that are opened when the system percolates provides an estimate of the percolation threshold.For example, if sites are opened in a 20-by-20 lattice according to the snapshots below, then our estimate of the percolation threshold is 204/400 = 0.51 because the system percolates when the 204th site is opened.
 |
 |
 |
 |
By repeating this computation experiment T times and averaging the results, we obtain a more accurate estimate of the percolation threshold. Let xt be the fraction of open sites in computational experiment t. The sample mean μ provides an estimate of the percolation threshold; the sample standard deviation σ measures the sharpness of the threshold.
Assuming T is sufficiently large (say, at least 30), the following provides a 95% confidence interval for the percolation threshold:
To perform a series of computational experiments, create a data type PercolationStats with the following API.
public class PercolationStats {
public PercolationStats(int N, int T) // perform T independent computational experiments on an N-by-N grid
public double mean() // sample mean of percolation threshold
public double stddev() // sample standard deviation of percolation threshold
public double confidenceLo() // returns lower bound of the 95% confidence interval
public double confidenceHi() // returns upper bound of the 95% confidence interval
public static void main(String[] args) // test client, described below
}
The constructor should throw a java.lang.IllegalArgumentException if either N ≤
0 or T ≤ 0.
Also, include a main() method that takes two command-line arguments N and T, performs T independent computational experiments (discussed above) on an N-by-N grid, and prints out the mean, standard deviation, and the 95% confidence interval for the percolation threshold. Use standard random from our standard libraries to generate random numbers; use standard statistics to compute the sample mean and standard deviation.
% java PercolationStats 200 100 mean = 0.5929934999999997 stddev = 0.00876990421552567 95% confidence interval = 0.5912745987737567, 0.5947124012262428 % java PercolationStats 200 100 mean = 0.592877 stddev = 0.009990523717073799 95% confidence interval = 0.5909188573514536, 0.5948351426485464 % java PercolationStats 2 10000 mean = 0.666925 stddev = 0.11776536521033558 95% confidence interval = 0.6646167988418774, 0.6692332011581226 % java PercolationStats 2 100000 mean = 0.6669475 stddev = 0.11775205263262094 95% confidence interval = 0.666217665216461, 0.6676773347835391
Analysis of running time and memory usage (optional and not graded). Implement the Percolation data type using the quick-find algorithm QuickFindUF.java from algs4.jar.
Use the stopwatch data type from our standard library to measure the total running time of PercolationStats. How does doubling N affect the total running time? How does doubling T affect the total running time? Give a formula (using tilde notation) of the total running time on your computer (in seconds) as a single function of both N and T. Using the 64-bit memory-cost model from lecture, give the total memory usage in bytes (using tilde notation) that a Percolation object uses to model an N-by-N percolation system. Count all memory that is used, including memory for the union-find data structure.Now, implement the Percolation data type using the weighted quick-union algorithm WeightedQuickUnionUF.java from algs4.jar. Answer the questions in the previous paragraph.
Deliverables. Submit only Percolation.java (using the weighted quick-union algorithm as implemented in the WeightedQuickUnionUF class) and PercolationStats.java. We will supply stdlib.jar and WeightedQuickUnionUF. Your submission may not call any library functions other than those in java.lang, stdlib.jar, and WeightedQuickUnionUF.
For fun. Create your own percolation input file and share it in the discussion forums. For some inspiration, see these nonogram puzzles.
This assignment was developed by Bob Sedgewick and Kevin Wayne.Copyright © 2008.
程式碼:
Percolation類
public class Percolation {
private UF uf;
private int N;
private int [][] map;
public Percolation(int N)
{
if (N <= 0)
throw new IllegalArgumentException();
this.N = N;
uf = new UF((N+2)*(N+2));
map = new int[N+2][N+2];
map[0][0] = 1;
map[N+1][0] = 1;
int i;
for(i = 1;i <= N;i++)
{
int index1 = N+2+i;
int index2 = 0;
uf.union(index1, index2);
}
for(i = 1;i <= N;i++)
{
int index1 = N*(N+2)+i;
int index2 = (N+1)*(N+2);
uf.union(index1, index2);
}
}
public void open(int i,int j)
{
if(i < 1 || i > N || j < 1 || j > N)
throw new IndexOutOfBoundsException();
int index1 = i*(N+2)+j;
int index2;
if(map[i][j] == 1)
return;
map[i][j] = 1;
if(i-1 >= 1)
{
if(map[i-1][j] == 1)
{
index2 = (i-1)*(N+2)+j;
uf.union(index1, index2);
}
}
if(i+1 <= N)
{
if(map[i+1][j] == 1)
{
index2 = (i+1)*(N+2)+j;
uf.union(index1, index2);
}
}
if(j-1 >= 1)
{
if(map[i][j-1] == 1)
{
index2 = i*(N+2)+j-1;
uf.union(index1, index2);
}
}
if(j+1 <= N)
{
if(map[i][j+1] == 1)
{
index2 = i*(N+2)+j+1;
uf.union(index1, index2);
}
}
}
public boolean isOpen(int i,int j)
{
if(i < 1 || i > N || j < 1 || j > N)
throw new IndexOutOfBoundsException();
if(map[i][j] == 1)
return true;
else
return false;
}
public boolean isFull(int i,int j)
{
if(i < 1 || i > N || j < 1 || j > N)
throw new IndexOutOfBoundsException();
if(N == 1)
return isOpen(1,1);
int k;
int index1 = i*(N+2)+j;
int index2 = 0;
if(isOpen(i,j))
return uf.connected(index1, index2);
else
return false;
}
public boolean percolates()
{
if(N == 1)
return isOpen(1,1);
int index1 = 0;
int index2 = (N+1)*(N+2);
return uf.connected(index1, index2);
}
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
//System.out.print("ni hao");
Percolation p = new Percolation(5);
//p.open(1, 1);
//p.open(1, 2);
p.open(1, 3);
p.open(2, 3);
p.open(3, 2);
p.open(2, 2);
p.open(5, 1);
p.open(4, 1);
p.open(3, 1);
for(int i = 1;i <= 5;i++)
{
for(int j = 1;j <=5;j++)
System.out.print(p.map[i][j]+" ");
System.out.print("\n");
}
for(int i = 1;i <= 5;i++)
{
for(int j = 1;j <=5;j++)
System.out.print(p.isFull(i,j)+" ");
System.out.print("\n");
}
System.out.print(p.percolates());
}
}PercolationStats類
import java.util.Random;
public class PercolationStats {
private int N;
private int T;
private long []count;
public PercolationStats(int N, int T)
{
if(N <= 0 || T <= 0)
throw new IllegalArgumentException();
count = new long[T];
this.N = N;
this.T = T;
for(int k = 0;k < T;k++)
{
Percolation p = new Percolation(N);
while(!p.percolates())
{
//Random random = new Random();
int i = (int) ((Math.random()*N)+1);
int j = (int) ((Math.random()*N)+1);
if(!p.isOpen(i, j))
{
p.open(i, j);
count[k]++;
}
}
}
}
public double mean()
{
double u;
long sum = 0;
for(int i = 0;i < T;i++)
sum += count[i];
u = (sum*1.0/T)/(N*N);
return u;
}
public double stddev()
{
double u = mean();
double sum = 0;
for(int i = 0;i < T;i++)
{
double x = count[i]*1.0/(N*N);
sum = sum + (x-u)*(x-u);
}
double stddev = Math.sqrt(sum/(T-1));
return stddev;
}
public double confidenceLo()
{
double u = mean();
double stddev = stddev();
double lo = u - (1.96*stddev/Math.sqrt(T));
return lo;
}
public double confidenceHi()
{
double u = mean();
double stddev = stddev();
double hi = u + (1.96*stddev/Math.sqrt(T));
return hi;
}
/**
* @param args
*/
public static void main(String[] args) {
// TODO Auto-generated method stub
//System.out.print("hello");
int N = Integer.parseInt(args[0]);
int T = Integer.parseInt(args[1]);
PercolationStats p = new PercolationStats(N,T);
System.out.print("mean:\t\t\t\t\t");
System.out.print("= "+p.mean()+"\n");
System.out.print("stddev:\t\t\t\t\t");
System.out.print("= "+p.stddev()+"\n");
System.out.print("95% confidence interval\t\t\t");
System.out.print("= "+p.confidenceLo()+",");
System.out.print(p.confidenceHi()+"\n");
}
}