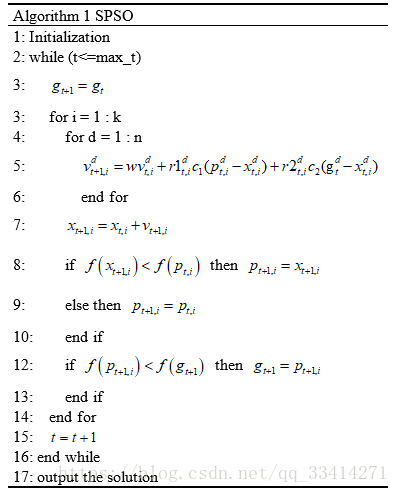背景

粒子群演算法最初是從研究鳥群捕食時得到的靈感，對於鳥群而言，如何在一大片區域中用有限的時間，最快地找到食物豐盛的領地，是一個決定鳥群生存繁衍的大問題。科學家們發現，單隻鳥所能搜尋的範圍十分有限，但整個鳥群卻像是被控制一般，很快聚集在食物最豐盛的地方。我們將每隻鳥抽象成一個“粒子”（particle），每個粒子都有自己的位置和速度，並記憶自己曾經飛過的最好位置和群體曾經飛過的最好位置，那麼在不斷迭代的過程中，整體鳥群就很可能向最優目標出飛去。

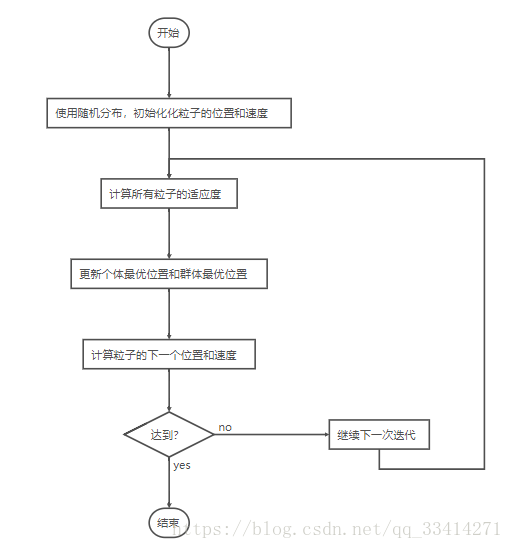
演算法的整個流程圖如下：

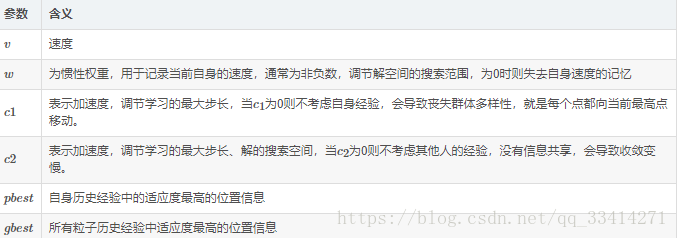
引數：

任務

實現下列程式碼：

where

# -*- coding: utf-8 -*-
"""
Created on Thu Jul 12 21:33:35 2018

@author: Liang Qingyuan
"""

import numpy as np  
import random   
import matplotlib.pyplot as plt  
import math 

#----------------------PSO引數設定---------------------------------  
class PSO():  
    def __init__(self,pN,dim,max_iter):  
        self.w = 1                  #慣性權重
        self.c1 = 1                 #pbest影響權重
        self.c2 = 1                 #gbest影響權重
        self.r1= random.uniform(0,1)#粒子的個體學習因子             
        self.r2= random.uniform(0,1)#社會的學習因子
        self.pN = pN                #粒子數量  
        self.dim = dim              #搜尋維度  
        self.max_iter = max_iter    #迭代次數  
        self.X = np.zeros((self.pN,self.dim))       #所有粒子的位置和速度  
        self.V = np.zeros((self.pN,self.dim))  
        self.pbest = np.zeros((self.pN,self.dim))   #個體經歷的最佳位置和全域性最佳位置  
        self.gbest = np.zeros((1,self.dim))  
        self.p_fit = np.zeros(self.pN)              #每個個體的歷史最佳適應值  
        self.fit = 1e10                             #全域性最佳適應值  
          
#---------------------目標函式------------------------------------  
    def function(self,x):  
        sum = 0  
        length = len(x)  
        x = x**2  
        for i in range(length):  
            sum += x[i]  
        return math.sqrt(sum)
#---------------------初始化種群----------------------------------  
    def init_Population(self):  
        for i in range(self.pN):  
            for j in range(self.dim):  
                self.X[i][j] = random.uniform(-10,10)  
                #self.V[i][j] = random.uniform(0,1)  
            self.pbest[i] = self.X[i]  
            tmp = self.function(self.X[i])  
            self.p_fit[i] = tmp  
            if(tmp < self.fit):  
                self.fit = tmp  
                self.gbest = self.X[i]  
      
#--------------------粒子迭代過程----------------------------------  
    def iterator(self):  
        fitness = []  
        f_gbest=[]
         #開始迭代
        for t in range(self.max_iter):             
            #更新速度和位置
            for i in range(self.pN): 
                for j in range(self.dim):
                    self.V[i][j] = self.w*self.V[i][j] + self.c1*self.r1*(self.pbest[i][j] - self.X[i][j]) + \
                            self.c2*self.r2*(self.gbest[j] - self.X[i][j])  
                
                #更新下一次迭代時的位置
                self.X[i] = self.X[i] + self.V[i]  
                
                #尋找最優解
                temp = self.function(self.X[i])  
                if(temp<self.p_fit[i]):             #更新個體最優#
                   self.p_fit[i] = temp             #個體最優結果
                   self.pbest[i] = self.X[i]        #個體最優位置
                   if(self.p_fit[i] < self.fit):    #更新全域性最優#  
                       self.gbest = self.X[i]       #全域性最優位置
                       self.fit = self.p_fit[i]     #全域性最優結果
            
            #確定目前最優值
            fitness.append(self.fit)
            f_gbest.append(self.gbest)
            print("#####fit#####",self.fit)                   #輸出最優值
            print("#####f-gbest#####",self.gbest)             #輸出最優值位置
        
        return fitness,f_gbest 
#----------------------程式執行-----------------------  
my_pso = PSO(pN=10,dim=5,max_iter=10000)  
my_pso.init_Population()  
fitness,f_gbest = my_pso.iterator()
#-----------------------效果展示--------------------------  
plt.figure(1)  
plt.title("Figure")  
plt.xlabel("iterators", size=14)  
plt.ylabel("fitness", size=14)  
t = np.array([t for t in range(0,10000)])  
fitness = np.array(fitness)  
plt.plot(t,fitness, color='b',linewidth=1)  
plt.show() 
 

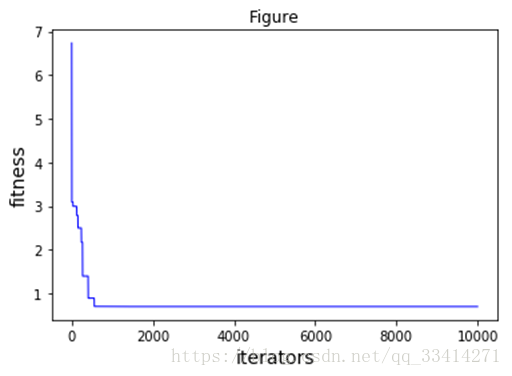
此次迭代過程：

最優值：0.7036775934527754

最優值時位置：[ -6.23916674   7.45154406 -19.60875577  -0.89308242   5.17591376]

參考文獻：

https://blog.csdn.net/as645788/article/details/70821430