matlab實現粒子群演算法
轉自:https://blog.csdn.net/nightmare_dimple/article/details/74331679
粒子群演算法(Particle Swarm Optimization,PSO)是20世紀90年代興起的一門學科,因其概念簡明、實現方便、收斂速度快而為人所知。粒子群演算法的基本思想是模擬鳥群隨機搜尋食物的捕食行為,鳥群通過自身經驗和種群之間的交流調整自己的搜尋路徑,從而找到食物最多的地點。其中每隻鳥的位置/路徑則為自變數組合,每次到達的地點的食物密度即函式值。每次搜尋都會根據自身經驗(自身歷史搜尋的最優地點)和種群交流(種群歷史搜尋的最優地點)調整自身搜尋方向和速度,這個稱為跟蹤極值,從而找到最優解。
粒子群演算法是一門新興演算法,此演算法與遺傳演算法有很多相似之處,其收斂於全域性最優解的概率很大。
①相較於傳統演算法計算速度非常快,全域性搜尋能力也很強;
②PSO對於種群大小不十分敏感,所以初始種群設為500-1000,速度影響也不大;
③粒子群演算法適用於連續函式極值問題,對於非線性、多峰問題均有較強的全域性搜尋能力。
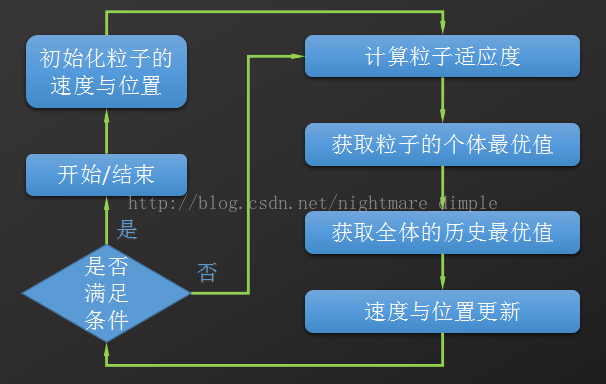
其流程圖如下:
迭代次數:一般取100~4000,太少解不穩定,太多浪費時間。對於複雜問題,進化代數可以相應地提高;
慣性權重:該引數反映了個體歷史成績對現在的影響,一般取0.5~1;
學習因子:一般取0~4,此處要根據自變數的取值範圍來定,並且學習因子分為個體和群體兩種;
空間維數:粒子搜尋的空間維數即為自變數的個數。
位置限制:
速度限制:如果粒子飛行速度過快,很可能直接飛過最優解位置,但是如果飛行速度過慢,會使得收斂速度變慢,因此設定合理的速度限制就很有必要了。
不同於遺傳演算法,粒子群演算法不需要編碼,直接利用粒子的位置來表示自變數,每個粒子的位置都由自變數的個數和取值範圍決定,而速度由自變數的個數和速度限制決定,形式如下,其中d代表空間維數(自變數數):

下面我們用一個例子來幫助理解,對於函式 f=x*sin(x)*cos(2*x)-2*x*sin(3*x) ,求其在區間[0,20]上該函式的最大值。首先我們需要畫出函式的影象,如下圖:
 多峰問題對於演算法的檢驗效果最佳,而上圖顯然是一個簡單的非等距、非等高的多峰一元函式。
多峰問題對於演算法的檢驗效果最佳,而上圖顯然是一個簡單的非等距、非等高的多峰一元函式。- 初始化種群
位置和速度的初始化即在位置和速度限制內隨機生成一個N x d 的矩陣,對於此題,位置初始化也就是在0~20內隨機生成一個50x1的資料矩陣,而對於速度則不用考慮約束,一般直接在0~1內隨機生成一個50x1的資料矩陣。
此處的位置約束也可以理解為位置限制,而速度限制是保證粒子步長不超限制的,一般設定速度限制為[-1,1]。 粒子群的另一個特點就是記錄每個個體的歷史最優和種群的歷史最優,因此而二者對應的最優位置和最優值也需要初始化。其中每個個體的歷史最優位置可以先初始化為當前位置,而種群的歷史最優位置則可初始化為原點。對於最優值,如果求最大值則初始化為負無窮,相反地初始化為正無窮。
每次搜尋都需要將當前的適應度和最優解同歷史的記錄值進行對比,如果超過歷史最優值,則更新個體和種群的歷史最優位置和最優解。
通過之前的引數設定可以得到如下的初始分佈圖:

- 速度與位置的更新
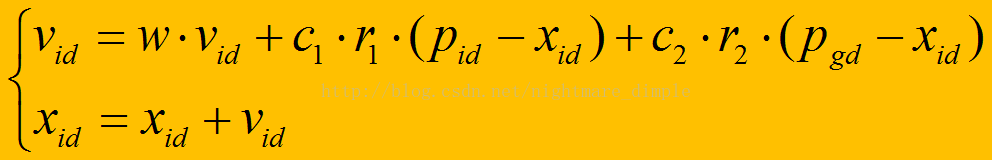

每次更新完速度和位置都需要考慮速度和位置的限制,需要將其限制在規定範圍內,此處僅舉出一個常規方法,即將超約束的資料約束到邊界(當位置或者速度超出初始化限制時,將其拉回靠近的邊界處)。當然,你不用擔心他會停住不動,因為每個粒子還有慣性和其他兩個引數的影響。
程式碼如下:[plain] view plain copy print?
- clc;clear;close all;
- %% 初始化種群
- f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函式表示式
- figure(1);ezplot(f,[0,0.01,20]);
- N = 50; % 初始種群個數
- d = 1; % 空間維數
- ger = 100; % 最大迭代次數
- limit = [0, 20]; % 設定位置引數限制
- vlimit = [-1, 1]; % 設定速度限制
- w = 0.8; % 慣性權重
- c1 = 0.5; % 自我學習因子
- c2 = 0.5; % 群體學習因子
- for i = 1:d
- x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始種群的位置
- end
- v = rand(N, d); % 初始種群的速度
- xm = x; % 每個個體的歷史最佳位置
- ym = zeros(1, d); % 種群的歷史最佳位置
- fxm = zeros(N, 1); % 每個個體的歷史最佳適應度
- fym = -inf; % 種群歷史最佳適應度
- hold on
- plot(xm, f(xm), 'ro');title('初始狀態圖');
- figure(2)
- %% 群體更新
- iter = 1;
- record = zeros(ger, 1); % 記錄器
- while iter <= ger
- fx = f(x) ; % 個體當前適應度
- for i = 1:N
- if fxm(i) < fx(i)
- fxm(i) = fx(i); % 更新個體歷史最佳適應度
- xm(i,:) = x(i,:); % 更新個體歷史最佳位置
- end
- end
- if fym < max(fxm)
- [fym, nmax] = max(fxm); % 更新群體歷史最佳適應度
- ym = xm(nmax, :); % 更新群體歷史最佳位置
- end
- v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
- % 邊界速度處理
- v(v > vlimit(2)) = vlimit(2);
- v(v < vlimit(1)) = vlimit(1);
- x = x + v;% 位置更新
- % 邊界位置處理
- x(x > limit(2)) = limit(2);
- x(x < limit(1)) = limit(1);
- record(iter) = fym;%最大值記錄
- % x0 = 0 : 0.01 : 20;
- % plot(x0, f(x0), 'b-', x, f(x), 'ro');title('狀態位置變化')
- % pause(0.1)
- iter = iter+1;
- end
- figure(3);plot(record);title('收斂過程')
- x0 = 0 : 0.01 : 20;
- figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最終狀態位置')
- disp(['最大值:',num2str(fym)]);
- disp(['變數取值:',num2str(ym)]);
clc;clear;close all;
%% 初始化種群
f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函式表示式
figure(1);ezplot(f,[0,0.01,20]);
N = 50; % 初始種群個數
d = 1; % 空間維數
ger = 100; % 最大迭代次數
limit = [0, 20]; % 設定位置引數限制
vlimit = [-1, 1]; % 設定速度限制
w = 0.8; % 慣性權重
c1 = 0.5; % 自我學習因子
c2 = 0.5; % 群體學習因子
for i = 1:d
x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始種群的位置
end
v = rand(N, d); % 初始種群的速度
xm = x; % 每個個體的歷史最佳位置
ym = zeros(1, d); % 種群的歷史最佳位置
fxm = zeros(N, 1); % 每個個體的歷史最佳適應度
fym = -inf; % 種群歷史最佳適應度
hold on
plot(xm, f(xm), 'ro');title('初始狀態圖');
figure(2)
%% 群體更新
iter = 1;
record = zeros(ger, 1); % 記錄器
while iter <= ger
fx = f(x) ; % 個體當前適應度
for i = 1:N
if fxm(i) < fx(i)
fxm(i) = fx(i); % 更新個體歷史最佳適應度
xm(i,:) = x(i,:); % 更新個體歷史最佳位置
end
end
if fym < max(fxm)
[fym, nmax] = max(fxm); % 更新群體歷史最佳適應度
ym = xm(nmax, :); % 更新群體歷史最佳位置
end
v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
% 邊界速度處理
v(v > vlimit(2)) = vlimit(2);
v(v < vlimit(1)) = vlimit(1);
x = x + v;% 位置更新
% 邊界位置處理
x(x > limit(2)) = limit(2);
x(x < limit(1)) = limit(1);
record(iter) = fym;%最大值記錄
% x0 = 0 : 0.01 : 20;
% plot(x0, f(x0), 'b-', x, f(x), 'ro');title('狀態位置變化')
% pause(0.1)
iter = iter+1;
end
figure(3);plot(record);title('收斂過程')
x0 = 0 : 0.01 : 20;
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最終狀態位置')
disp(['最大值:',num2str(fym)]);
disp(['變數取值:',num2str(ym)]); 由上圖可以看出演算法已成功找出了最優解,其最優解為18.3014,而其最大值為32.1462。
由上圖可以看出演算法已成功找出了最優解,其最優解為18.3014,而其最大值為32.1462。如果想看粒子群演算法中粒子的搜尋過程的可以將程式碼中註釋掉的三行程式碼放上去。效果是這樣的:

將粒子群的搜尋過程可視化了,並將其轉存為了gif格式檔案:
1.首先pause(),是在每次繪圖之後暫停一段時間,單位是秒,再進行下一次繪圖;
2.而當要轉存為gif檔案時,這其實就是一種無聲的視訊檔案,因此我們需要每一幀的影象,可以用pause,但是用drawnow更好,它的原理是保持當前視窗不變,繼續下一次繪圖。
因此將轉存為gif的步驟加入到之前的程式碼中就是:
[plain] view plain copy print?- clc;clear;close all;
- %% 初始化種群
- f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函式表示式
- N = 50; % 初始種群個數
- d = 1; % 空間維數
- ger = 100; % 最大迭代次數
- limit = [0, 20]; % 設定位置引數限制
- vlimit = [-1, 1]; % 設定速度限制
- w = 0.8; % 慣性權重
- c1 = 0.5; % 自我學習因子
- c2 = 0.5; % 群體學習因子
- for i = 1:d
- x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始種群的位置
- end
- v = rand(N, d); % 初始種群的速度
- xm = x; % 每個個體的歷史最佳位置
- ym = zeros(1, d); % 種群的歷史最佳位置
- fxm = zeros(N, 1); % 每個個體的歷史最佳適應度
- fym = -inf; % 種群歷史最佳適應度
- %% 群體更新
- iter = 1;
- record = zeros(ger, 1); % 記錄器
- while iter <= ger
- fx = f(x) ; % 個體當前適應度
- for i = 1:N
- if fxm(i) < fx(i)
- fxm(i) = fx(i); % 更新個體歷史最佳適應度
- xm(i,:) = x(i,:); % 更新個體歷史最佳位置
- end
- end
- if fym < max(fxm)
- [fym, nmax] = max(fxm); % 更新群體歷史最佳適應度
- ym = xm(nmax, :); % 更新群體歷史最佳位置
- end
- v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
- % 邊界速度處理
- v(v > vlimit(2)) = vlimit(2);
- v(v < vlimit(1)) = vlimit(1);
- x = x + v;% 位置更新
- % 邊界位置處理
- x(x > limit(2)) = limit(2);
- x(x < limit(1)) = limit(1);
- record(iter) = fym;%最大值記錄
- x0 = 0 : 0.01 : 20;
- plot(x0, f(x0), 'b-', x, f(x), 'ro');title('狀態位置變化')
- drawnow
- frame = getframe(1);
- im = frame2im(frame);
- [A,map] = rgb2ind(im,256);
- if iter == 1;
- imwrite(A,map,'E:\培訓\優化演算法\pso.gif','gif','LoopCount',Inf,'DelayTime',0.1);
- else
- imwrite(A,map,'E:\培訓\優化演算法\pso.gif','gif','WriteMode','append','DelayTime',0.1);
- end
- iter = iter+1;
- end
- disp(['最大值:',num2str(fym)]);
- disp(['變數取值:',num2str(ym)]);
clc;clear;close all;
%% 初始化種群
f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函式表示式
N = 50; % 初始種群個數
d = 1; % 空間維數
ger = 100; % 最大迭代次數
limit = [0, 20]; % 設定位置引數限制
vlimit = [-1, 1]; % 設定速度限制
w = 0.8; % 慣性權重
c1 = 0.5; % 自我學習因子
c2 = 0.5; % 群體學習因子
for i = 1:d
x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始種群的位置
end
v = rand(N, d); % 初始種群的速度
xm = x; % 每個個體的歷史最佳位置
ym = zeros(1, d); % 種群的歷史最佳位置
fxm = zeros(N, 1); % 每個個體的歷史最佳適應度
fym = -inf; % 種群歷史最佳適應度
%% 群體更新
iter = 1;
record = zeros(ger, 1); % 記錄器
while iter <= ger
fx = f(x) ; % 個體當前適應度
for i = 1:N
if fxm(i) < fx(i)
fxm(i) = fx(i); % 更新個體歷史最佳適應度
xm(i,:) = x(i,:); % 更新個體歷史最佳位置
end
end
if fym < max(fxm)
[fym, nmax] = max(fxm); % 更新群體歷史最佳適應度
ym = xm(nmax, :); % 更新群體歷史最佳位置
end
v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
% 邊界速度處理
v(v > vlimit(2)) = vlimit(2);
v(v < vlimit(1)) = vlimit(1);
x = x + v;% 位置更新
% 邊界位置處理
x(x > limit(2)) = limit(2);
x(x < limit(1)) = limit(1);
record(iter) = fym;%最大值記錄
x0 = 0 : 0.01 : 20;
plot(x0, f(x0), 'b-', x, f(x), 'ro');title('狀態位置變化')
drawnow
frame = getframe(1);
im = frame2im(frame);
[A,map] = rgb2ind(im,256);
if iter == 1;
imwrite(A,map,'E:\培訓\優化演算法\pso.gif','gif','LoopCount',Inf,'DelayTime',0.1);
else
imwrite(A,map,'E:\培訓\優化演算法\pso.gif','gif','WriteMode','append','DelayTime',0.1);
end
iter = iter+1;
end
disp(['最大值:',num2str(fym)]);
disp(['變數取值:',num2str(ym)]);另外,大家可以看到,種群歷史最優值處我們初始化為了-inf,這是因為我們需要求最大值。但是如果要求最小值應該怎麼辦呢?最好不要將這裡改成+inf,如果這樣做,我們後面的最優值更新中全部要改成最小值和<,太麻煩。那麼最好的方式就是直接在適應度處加上負號,這樣的話就相當於求最小值了,只不過要將最後的最優值取反。
並且我們之前所寫的只是一維問題優化,程式碼優化程度不高,對此我給出一份優化程度較高的程式碼,以應對多維優化問題:
問題是求21.5+x*sin(4*pi*x)+y*sin(20*pi*y),x=[-3,12.1];y=[4.1,5.8]的極值。
[plain] view plain copy print?- clc;clear;close all;tic
- %% 引數設定
- N = 500;
- d = 2;
- ger = 1000;
- w = 0.8;
- c1 = 0.9;
- c2 = 0.9;
- xlimit = [-3 12.1;4.1 5.8];
- vlimit = [-1 1;-1 1];
- %% 種群初始化
- x = repmat(xlimit(:,1)',N,1)+repmat(diff(xlimit'),N,1).*rand(N,d);
- v = repmat(vlimit(:,1)',N,1)+repmat(diff(vlimit'),N,1).*rand(N,d);
- xm = x;
- fxm = -inf*ones(N,1);
- ym = xlimit(:,1)'+diff(xlimit').*rand(1,d);
- fym = -inf;
- %% 開始搜尋
- for i = 1 : ger
- y = f(x);
- for j = 1 : N
- if y(j)>fxm(j)
- fxm(j)=y(j);
- xm(j,:) = x(j,:);
- if y(j)>fym
- fym = y(j);
- ym = x(j,:);
- end
- end
- end
- v = w*v+c1*rand*(xm-x)+c2*rand*(repmat(ym,N,1)-x);
- x = x+v;
- x = min(x,repmat(xlimit(:,2)',N,1));
- x = max(x,repmat(xlimit(:,1)',N,1));
- v = min(v,repmat(vlimit(:,2)',N,1));
- v = max(v,repmat(vlimit(:,1)',N,1));
- end
- toc
- disp(['最優解為:',num2str(ym)]);
- disp(['最優值為:',num2str(fym)]);
clc;clear;close all;tic
%% 引數設定
N = 500;
d = 2;
ger = 1000;
w = 0.8;
c1 = 0.9;
c2 = 0.9;
xlimit = [-3 12.1;4.1 5.8];
vlimit = [-1 1;-1 1];
%% 種群初始化
x = repmat(xlimit(:,1)',N,1)+repmat(diff(xlimit'),N,1).*rand(N,d);
v = repmat(vlimit(:,1)',N,1)+repmat(diff(vlimit'),N,1).*rand(N,d);
xm = x;
fxm = -inf*ones(N,1);
ym = xlimit(:,1)'+diff(xlimit').*rand(1,d);
fym = -inf;
%% 開始搜尋
for i = 1 : ger
y = f(x);
for j = 1 : N
if y(j)>fxm(j)
fxm(j)=y(j);
xm(j,:) = x(j,:);
if y(j)>fym
fym = y(j);
ym = x(j,:);
end
end
end
v = w*v+c1*rand*(xm-x)+c2*rand*(repmat(ym,N,1)-x);
x = x+v;
x = min(x,repmat(xlimit(:,2)',N,1));
x = max(x,repmat(xlimit(:,1)',N,1));
v = min(v,repmat(vlimit(:,2)',N,1));
v = max(v,repmat(vlimit(:,1)',N,1));
end
toc
disp(['最優解為:',num2str(ym)]);
disp(['最優值為:',num2str(fym)]);
- function y = f(x)
- y = 21.5+x(:,1).*sin(4*pi*x(:,1))+x(:,2).*sin(20*pi*x(:,2));
- end