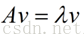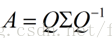2. 程式人生 > >機器學習知識點(十九)矩陣特徵值分解基礎知識及Java實現

機器學習知識點(十九)矩陣特徵值分解基礎知識及Java實現

阿新 • • 發佈：2019-01-01

1、特徵值分解基礎知識

矩陣乘法Y=AB的數學意義在於變換，以其中一個向量A為中心，則B的作用主要是使A發生伸縮或旋轉變換。一個矩陣其實就是一個線性變換，因為一個矩陣乘以一個向量後得到的向量，其實就相當於將這個向量進行了線性變換。

如果說一個向量v是方陣A的特徵向量，將一定可以表示成下面的形式：


    這時候λ就被稱為特徵向量v對應的特徵值，一個矩陣的一組特徵向量是一組正交向量。特徵值分解是將一個矩陣分解成下面的形式：


其中Q是這個矩陣A的特徵向量組成的矩陣，Σ是一個對角陣，每一個對角線上的元素就是一個特徵值。一個變換方陣的所有特徵向量組成了這個變換矩陣的一組基。所謂基，可以理解為座標系的軸。平常用到直角座標系，線上性代數中可以把這個座標系扭曲、拉伸、旋轉，稱為基變換。可以按需求去設定基，但是基的軸之間必須是線性無關的，也就是保證座標系的不同軸不要指向同一個方向或可以被別的軸組合而成。從線性空間的角度看，在一個定義了內積的線性空間裡，對一個N階對稱方陣進行特徵分解，就是產生了該空間的N個標準正交基，然後把矩陣投影到這N個基上。N個特徵向量就是N個標準正交基，而特徵值的模則代表矩陣在每個基上的投影長度。特徵值越大，說明矩陣在對應的特徵向量上的方差越大，功率越大，資訊量越多。不過，特徵值分解也有很多的侷限，比如說變換的矩陣必須是方陣。

在機器學習特徵提取中，意思就是最大特徵值對應的特徵向量方向上包含最多的資訊量，如果某幾個特徵值很小，說明這幾個方向資訊量很小，可以用來降維，也就是刪除小特徵值對應方向的資料，只保留大特徵值方向對應的資料，這樣做以後資料量減小，但有用資訊量變化不大，PCA降維就是基於這種思路。特徵值分解可以得到特徵值與特徵向量，特徵值表示的是這個特徵到底有多重要，而特徵向量表示這個特徵是什麼，可以將每一個特徵向量理解為一個線性的子空間。

2、Java實現

下載Jama-1.0.3.zip研究原始碼。

1）  特徵值分解測試類

package sk.ml;

import Jama.EigenvalueDecomposition;
import Jama.Matrix;

public class QRTest {
	//矩陣特徵分解
	public static void main(String argv[]){
		double[] columnwise = {1.,2.,3.,4.,5.,6.,7.,8.,9.,10.,11.,12.};
		Matrix A = new Matrix(columnwise,4);//構造矩陣
		A.print(A.getColumnDimension(), A.getRowDimension());
		EigenvalueDecomposition Eig = A.eig();
	    Matrix D = Eig.getD();
	    Matrix V = Eig.getV();
		D.print(D.getColumnDimension(), D.getRowDimension());//列印特徵值
		V.print(V.getColumnDimension(), V.getRowDimension());//列印特徵向量
	}
}

2）  原始碼參考Matrix

package Jama;

import java.text.NumberFormat;
import java.text.DecimalFormat;
import java.text.DecimalFormatSymbols;
import java.util.Locale;
import java.text.FieldPosition;
import java.io.PrintWriter;
import java.io.BufferedReader;
import java.io.StreamTokenizer;
import Jama.util.*;

/**
   Jama = Java Matrix class.
<P>
   The Java Matrix Class provides the fundamental operations of numerical
   linear algebra.  Various constructors create Matrices from two dimensional
   arrays of double precision floating point numbers.  Various "gets" and
   "sets" provide access to submatrices and matrix elements.  Several methods 
   implement basic matrix arithmetic, including matrix addition and
   multiplication, matrix norms, and element-by-element array operations.
   Methods for reading and printing matrices are also included.  All the
   operations in this version of the Matrix Class involve real matrices.
   Complex matrices may be handled in a future version.
<P>
   Five fundamental matrix decompositions, which consist of pairs or triples
   of matrices, permutation vectors, and the like, produce results in five
   decomposition classes.  These decompositions are accessed by the Matrix
   class to compute solutions of simultaneous linear equations, determinants,
   inverses and other matrix functions.  The five decompositions are:
<P><UL>
   <LI>Cholesky Decomposition of symmetric, positive definite matrices.
   <LI>LU Decomposition of rectangular matrices.
   <LI>QR Decomposition of rectangular matrices.
   <LI>Singular Value Decomposition of rectangular matrices.
   <LI>Eigenvalue Decomposition of both symmetric and nonsymmetric square matrices.
</UL>
<DL>
<DT><B>Example of use:</B></DT>
<P>
<DD>Solve a linear system A x = b and compute the residual norm, ||b - A x||.
<P><PRE>
      double[][] vals = {{1.,2.,3},{4.,5.,6.},{7.,8.,10.}};
      Matrix A = new Matrix(vals);
      Matrix b = Matrix.random(3,1);
      Matrix x = A.solve(b);
      Matrix r = A.times(x).minus(b);
      double rnorm = r.normInf();
</PRE></DD>
</DL>

@author The MathWorks, Inc. and the National Institute of Standards and Technology.
@version 5 August 1998
*/

public class Matrix implements Cloneable, java.io.Serializable {

/* ------------------------
   Class variables
 * ------------------------ */

   /** Array for internal storage of elements.
   @serial internal array storage.
   */
   private double[][] A;

   /** Row and column dimensions.
   @serial row dimension.
   @serial column dimension.
   */
   private int m, n;

/* ------------------------
   Constructors
 * ------------------------ */

   /** Construct an m-by-n matrix of zeros. 
   @param m    Number of rows.
   @param n    Number of colums.
   */

   public Matrix (int m, int n) {
      this.m = m;
      this.n = n;
      A = new double[m][n];
   }

   /** Construct an m-by-n constant matrix.
   @param m    Number of rows.
   @param n    Number of colums.
   @param s    Fill the matrix with this scalar value.
   */

   public Matrix (int m, int n, double s) {
      this.m = m;
      this.n = n;
      A = new double[m][n];
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = s;
         }
      }
   }

   /** Construct a matrix from a 2-D array.
   @param A    Two-dimensional array of doubles.
   @exception  IllegalArgumentException All rows must have the same length
   @see        #constructWithCopy
   */

   public Matrix (double[][] A) {
      m = A.length;
      n = A[0].length;
      for (int i = 0; i < m; i++) {
         if (A[i].length != n) {
            throw new IllegalArgumentException("All rows must have the same length.");
         }
      }
      this.A = A;
   }

   /** Construct a matrix quickly without checking arguments.
   @param A    Two-dimensional array of doubles.
   @param m    Number of rows.
   @param n    Number of colums.
   */

   public Matrix (double[][] A, int m, int n) {
      this.A = A;
      this.m = m;
      this.n = n;
   }

   /** Construct a matrix from a one-dimensional packed array
   @param vals One-dimensional array of doubles, packed by columns (ala Fortran).
   @param m    Number of rows.
   @exception  IllegalArgumentException Array length must be a multiple of m.
   */

   public Matrix (double vals[], int m) {
      this.m = m;
      n = (m != 0 ? vals.length/m : 0);
      if (m*n != vals.length) {
         throw new IllegalArgumentException("Array length must be a multiple of m.");
      }
      A = new double[m][n];
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = vals[i+j*m];
         }
      }
   }

/* ------------------------
   Public Methods
 * ------------------------ */

   /** Construct a matrix from a copy of a 2-D array.
   @param A    Two-dimensional array of doubles.
   @exception  IllegalArgumentException All rows must have the same length
   */

   public static Matrix constructWithCopy(double[][] A) {
      int m = A.length;
      int n = A[0].length;
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         if (A[i].length != n) {
            throw new IllegalArgumentException
               ("All rows must have the same length.");
         }
         for (int j = 0; j < n; j++) {
            C[i][j] = A[i][j];
         }
      }
      return X;
   }

   /** Make a deep copy of a matrix
   */

   public Matrix copy () {
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = A[i][j];
         }
      }
      return X;
   }

   /** Clone the Matrix object.
   */

   public Object clone () {
      return this.copy();
   }

   /** Access the internal two-dimensional array.
   @return     Pointer to the two-dimensional array of matrix elements.
   */

   public double[][] getArray () {
      return A;
   }

   /** Copy the internal two-dimensional array.
   @return     Two-dimensional array copy of matrix elements.
   */

   public double[][] getArrayCopy () {
      double[][] C = new double[m][n];
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = A[i][j];
         }
      }
      return C;
   }

   /** Make a one-dimensional column packed copy of the internal array.
   @return     Matrix elements packed in a one-dimensional array by columns.
   */

   public double[] getColumnPackedCopy () {
      double[] vals = new double[m*n];
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            vals[i+j*m] = A[i][j];
         }
      }
      return vals;
   }

   /** Make a one-dimensional row packed copy of the internal array.
   @return     Matrix elements packed in a one-dimensional array by rows.
   */

   public double[] getRowPackedCopy () {
      double[] vals = new double[m*n];
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            vals[i*n+j] = A[i][j];
         }
      }
      return vals;
   }

   /** Get row dimension.
   @return     m, the number of rows.
   */

   public int getRowDimension () {
      return m;
   }

   /** Get column dimension.
   @return     n, the number of columns.
   */

   public int getColumnDimension () {
      return n;
   }

   /** Get a single element.
   @param i    Row index.
   @param j    Column index.
   @return     A(i,j)
   @exception  ArrayIndexOutOfBoundsException
   */

   public double get (int i, int j) {
      return A[i][j];
   }

   /** Get a submatrix.
   @param i0   Initial row index
   @param i1   Final row index
   @param j0   Initial column index
   @param j1   Final column index
   @return     A(i0:i1,j0:j1)
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public Matrix getMatrix (int i0, int i1, int j0, int j1) {
      Matrix X = new Matrix(i1-i0+1,j1-j0+1);
      double[][] B = X.getArray();
      try {
         for (int i = i0; i <= i1; i++) {
            for (int j = j0; j <= j1; j++) {
               B[i-i0][j-j0] = A[i][j];
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
      return X;
   }

   /** Get a submatrix.
   @param r    Array of row indices.
   @param c    Array of column indices.
   @return     A(r(:),c(:))
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public Matrix getMatrix (int[] r, int[] c) {
      Matrix X = new Matrix(r.length,c.length);
      double[][] B = X.getArray();
      try {
         for (int i = 0; i < r.length; i++) {
            for (int j = 0; j < c.length; j++) {
               B[i][j] = A[r[i]][c[j]];
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
      return X;
   }

   /** Get a submatrix.
   @param i0   Initial row index
   @param i1   Final row index
   @param c    Array of column indices.
   @return     A(i0:i1,c(:))
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public Matrix getMatrix (int i0, int i1, int[] c) {
      Matrix X = new Matrix(i1-i0+1,c.length);
      double[][] B = X.getArray();
      try {
         for (int i = i0; i <= i1; i++) {
            for (int j = 0; j < c.length; j++) {
               B[i-i0][j] = A[i][c[j]];
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
      return X;
   }

   /** Get a submatrix.
   @param r    Array of row indices.
   @param j0   Initial column index
   @param j1   Final column index
   @return     A(r(:),j0:j1)
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public Matrix getMatrix (int[] r, int j0, int j1) {
      Matrix X = new Matrix(r.length,j1-j0+1);
      double[][] B = X.getArray();
      try {
         for (int i = 0; i < r.length; i++) {
            for (int j = j0; j <= j1; j++) {
               B[i][j-j0] = A[r[i]][j];
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
      return X;
   }

   /** Set a single element.
   @param i    Row index.
   @param j    Column index.
   @param s    A(i,j).
   @exception  ArrayIndexOutOfBoundsException
   */

   public void set (int i, int j, double s) {
      A[i][j] = s;
   }

   /** Set a submatrix.
   @param i0   Initial row index
   @param i1   Final row index
   @param j0   Initial column index
   @param j1   Final column index
   @param X    A(i0:i1,j0:j1)
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public void setMatrix (int i0, int i1, int j0, int j1, Matrix X) {
      try {
         for (int i = i0; i <= i1; i++) {
            for (int j = j0; j <= j1; j++) {
               A[i][j] = X.get(i-i0,j-j0);
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
   }

   /** Set a submatrix.
   @param r    Array of row indices.
   @param c    Array of column indices.
   @param X    A(r(:),c(:))
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public void setMatrix (int[] r, int[] c, Matrix X) {
      try {
         for (int i = 0; i < r.length; i++) {
            for (int j = 0; j < c.length; j++) {
               A[r[i]][c[j]] = X.get(i,j);
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
   }

   /** Set a submatrix.
   @param r    Array of row indices.
   @param j0   Initial column index
   @param j1   Final column index
   @param X    A(r(:),j0:j1)
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public void setMatrix (int[] r, int j0, int j1, Matrix X) {
      try {
         for (int i = 0; i < r.length; i++) {
            for (int j = j0; j <= j1; j++) {
               A[r[i]][j] = X.get(i,j-j0);
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
   }

   /** Set a submatrix.
   @param i0   Initial row index
   @param i1   Final row index
   @param c    Array of column indices.
   @param X    A(i0:i1,c(:))
   @exception  ArrayIndexOutOfBoundsException Submatrix indices
   */

   public void setMatrix (int i0, int i1, int[] c, Matrix X) {
      try {
         for (int i = i0; i <= i1; i++) {
            for (int j = 0; j < c.length; j++) {
               A[i][c[j]] = X.get(i-i0,j);
            }
         }
      } catch(ArrayIndexOutOfBoundsException e) {
         throw new ArrayIndexOutOfBoundsException("Submatrix indices");
      }
   }

   /** Matrix transpose.
   @return    A'
   */

   public Matrix transpose () {
      Matrix X = new Matrix(n,m);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[j][i] = A[i][j];
         }
      }
      return X;
   }

   /** One norm
   @return    maximum column sum.
   */

   public double norm1 () {
      double f = 0;
      for (int j = 0; j < n; j++) {
         double s = 0;
         for (int i = 0; i < m; i++) {
            s += Math.abs(A[i][j]);
         }
         f = Math.max(f,s);
      }
      return f;
   }

   /** Two norm
   @return    maximum singular value.
   */

   public double norm2 () {
      return (new SingularValueDecomposition(this).norm2());
   }

   /** Infinity norm
   @return    maximum row sum.
   */

   public double normInf () {
      double f = 0;
      for (int i = 0; i < m; i++) {
         double s = 0;
         for (int j = 0; j < n; j++) {
            s += Math.abs(A[i][j]);
         }
         f = Math.max(f,s);
      }
      return f;
   }

   /** Frobenius norm
   @return    sqrt of sum of squares of all elements.
   */

   public double normF () {
      double f = 0;
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            f = Maths.hypot(f,A[i][j]);
         }
      }
      return f;
   }

   /**  Unary minus
   @return    -A
   */

   public Matrix uminus () {
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = -A[i][j];
         }
      }
      return X;
   }

   /** C = A + B
   @param B    another matrix
   @return     A + B
   */

   public Matrix plus (Matrix B) {
      checkMatrixDimensions(B);
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = A[i][j] + B.A[i][j];
         }
      }
      return X;
   }

   /** A = A + B
   @param B    another matrix
   @return     A + B
   */

   public Matrix plusEquals (Matrix B) {
      checkMatrixDimensions(B);
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = A[i][j] + B.A[i][j];
         }
      }
      return this;
   }

   /** C = A - B
   @param B    another matrix
   @return     A - B
   */

   public Matrix minus (Matrix B) {
      checkMatrixDimensions(B);
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = A[i][j] - B.A[i][j];
         }
      }
      return X;
   }

   /** A = A - B
   @param B    another matrix
   @return     A - B
   */

   public Matrix minusEquals (Matrix B) {
      checkMatrixDimensions(B);
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = A[i][j] - B.A[i][j];
         }
      }
      return this;
   }

   /** Element-by-element multiplication, C = A.*B
   @param B    another matrix
   @return     A.*B
   */

   public Matrix arrayTimes (Matrix B) {
      checkMatrixDimensions(B);
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = A[i][j] * B.A[i][j];
         }
      }
      return X;
   }

   /** Element-by-element multiplication in place, A = A.*B
   @param B    another matrix
   @return     A.*B
   */

   public Matrix arrayTimesEquals (Matrix B) {
      checkMatrixDimensions(B);
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = A[i][j] * B.A[i][j];
         }
      }
      return this;
   }

   /** Element-by-element right division, C = A./B
   @param B    another matrix
   @return     A./B
   */

   public Matrix arrayRightDivide (Matrix B) {
      checkMatrixDimensions(B);
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = A[i][j] / B.A[i][j];
         }
      }
      return X;
   }

   /** Element-by-element right division in place, A = A./B
   @param B    another matrix
   @return     A./B
   */

   public Matrix arrayRightDivideEquals (Matrix B) {
      checkMatrixDimensions(B);
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = A[i][j] / B.A[i][j];
         }
      }
      return this;
   }

   /** Element-by-element left division, C = A.\B
   @param B    another matrix
   @return     A.\B
   */

   public Matrix arrayLeftDivide (Matrix B) {
      checkMatrixDimensions(B);
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = B.A[i][j] / A[i][j];
         }
      }
      return X;
   }

   /** Element-by-element left division in place, A = A.\B
   @param B    another matrix
   @return     A.\B
   */

   public Matrix arrayLeftDivideEquals (Matrix B) {
      checkMatrixDimensions(B);
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = B.A[i][j] / A[i][j];
         }
      }
      return this;
   }

   /** Multiply a matrix by a scalar, C = s*A
   @param s    scalar
   @return     s*A
   */

   public Matrix times (double s) {
      Matrix X = new Matrix(m,n);
      double[][] C = X.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            C[i][j] = s*A[i][j];
         }
      }
      return X;
   }

   /** Multiply a matrix by a scalar in place, A = s*A
   @param s    scalar
   @return     replace A by s*A
   */

   public Matrix timesEquals (double s) {
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            A[i][j] = s*A[i][j];
         }
      }
      return this;
   }

   /** Linear algebraic matrix multiplication, A * B
   @param B    another matrix
   @return     Matrix product, A * B
   @exception  IllegalArgumentException Matrix inner dimensions must agree.
   */

   public Matrix times (Matrix B) {
      if (B.m != n) {
         throw new IllegalArgumentException("Matrix inner dimensions must agree.");
      }
      Matrix X = new Matrix(m,B.n);
      double[][] C = X.getArray();
      double[] Bcolj = new double[n];
      for (int j = 0; j < B.n; j++) {
         for (int k = 0; k < n; k++) {
            Bcolj[k] = B.A[k][j];
         }
         for (int i = 0; i < m; i++) {
            double[] Arowi = A[i];
            double s = 0;
            for (int k = 0; k < n; k++) {
               s += Arowi[k]*Bcolj[k];
            }
            C[i][j] = s;
         }
      }
      return X;
   }

   /** LU Decomposition
   @return     LUDecomposition
   @see LUDecomposition
   */

   public LUDecomposition lu () {
      return new LUDecomposition(this);
   }

   /** QR Decomposition
   @return     QRDecomposition
   @see QRDecomposition
   */

   public QRDecomposition qr () {
      return new QRDecomposition(this);
   }

   /** Cholesky Decomposition
   @return     CholeskyDecomposition
   @see CholeskyDecomposition
   */

   public CholeskyDecomposition chol () {
      return new CholeskyDecomposition(this);
   }

   /** Singular Value Decomposition
   @return     SingularValueDecomposition
   @see SingularValueDecomposition
   */

   public SingularValueDecomposition svd () {
      return new SingularValueDecomposition(this);
   }

   /** Eigenvalue Decomposition
   @return     EigenvalueDecomposition
   @see EigenvalueDecomposition
   */

   public EigenvalueDecomposition eig () {
      return new EigenvalueDecomposition(this);
   }

   /** Solve A*X = B
   @param B    right hand side
   @return     solution if A is square, least squares solution otherwise
   */

   public Matrix solve (Matrix B) {
      return (m == n ? (new LUDecomposition(this)).solve(B) :
                       (new QRDecomposition(this)).solve(B));
   }

   /** Solve X*A = B, which is also A'*X' = B'
   @param B    right hand side
   @return     solution if A is square, least squares solution otherwise.
   */

   public Matrix solveTranspose (Matrix B) {
      return transpose().solve(B.transpose());
   }

   /** Matrix inverse or pseudoinverse
   @return     inverse(A) if A is square, pseudoinverse otherwise.
   */

   public Matrix inverse () {
      return solve(identity(m,m));
   }

   /** Matrix determinant
   @return     determinant
   */

   public double det () {
      return new LUDecomposition(this).det();
   }

   /** Matrix rank
   @return     effective numerical rank, obtained from SVD.
   */

   public int rank () {
      return new SingularValueDecomposition(this).rank();
   }

   /** Matrix condition (2 norm)
   @return     ratio of largest to smallest singular value.
   */

   public double cond () {
      return new SingularValueDecomposition(this).cond();
   }

   /** Matrix trace.
   @return     sum of the diagonal elements.
   */

   public double trace () {
      double t = 0;
      for (int i = 0; i < Math.min(m,n); i++) {
         t += A[i][i];
      }
      return t;
   }

   /** Generate matrix with random elements
   @param m    Number of rows.
   @param n    Number of colums.
   @return     An m-by-n matrix with uniformly distributed random elements.
   */

   public static Matrix random (int m, int n) {
      Matrix A = new Matrix(m,n);
      double[][] X = A.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            X[i][j] = Math.random();
         }
      }
      return A;
   }

   /** Generate identity matrix
   @param m    Number of rows.
   @param n    Number of colums.
   @return     An m-by-n matrix with ones on the diagonal and zeros elsewhere.
   */

   public static Matrix identity (int m, int n) {
      Matrix A = new Matrix(m,n);
      double[][] X = A.getArray();
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            X[i][j] = (i == j ? 1.0 : 0.0);
         }
      }
      return A;
   }


   /** Print the matrix to stdout.   Line the elements up in columns
     * with a Fortran-like 'Fw.d' style format.
   @param w    Column width.
   @param d    Number of digits after the decimal.
   */

   public void print (int w, int d) {
      print(new PrintWriter(System.out,true),w,d); }

   /** Print the matrix to the output stream.   Line the elements up in
     * columns with a Fortran-like 'Fw.d' style format.
   @param output Output stream.
   @param w      Column width.
   @param d      Number of digits after the decimal.
   */

   public void print (PrintWriter output, int w, int d) {
      DecimalFormat format = new DecimalFormat();
      format.setDecimalFormatSymbols(new DecimalFormatSymbols(Locale.US));
      format.setMinimumIntegerDigits(1);
      format.setMaximumFractionDigits(d);
      format.setMinimumFractionDigits(d);
      format.setGroupingUsed(false);
      print(output,format,w+2);
   }

   /** Print the matrix to stdout.  Line the elements up in columns.
     * Use the format object, and right justify within columns of width
     * characters.
     * Note that is the matrix is to be read back in, you probably will want
     * to use a NumberFormat that is set to US Locale.
   @param format A  Formatting object for individual elements.
   @param width     Field width for each column.
   @see java.text.DecimalFormat#setDecimalFormatSymbols
   */

   public void print (NumberFormat format, int width) {
      print(new PrintWriter(System.out,true),format,width); }

   // DecimalFormat is a little disappointing coming from Fortran or C's printf.
   // Since it doesn't pad on the left, the elements will come out different
   // widths.  Consequently, we'll pass the desired column width in as an
   // argument and do the extra padding ourselves.

   /** Print the matrix to the output stream.  Line the elements up in columns.
     * Use the format object, and right justify within columns of width
     * characters.
     * Note that is the matrix is to be read back in, you probably will want
     * to use a NumberFormat that is set to US Locale.
   @param output the output stream.
   @param format A formatting object to format the matrix elements 
   @param width  Column width.
   @see java.text.DecimalFormat#setDecimalFormatSymbols
   */

   public void print (PrintWriter output, NumberFormat format, int width) {
      output.println();  // start on new line.
      for (int i = 0; i < m; i++) {
         for (int j = 0; j < n; j++) {
            String s = format.format(A[i][j]); // format the number
            int padding = Math.max(1,width-s.length()); // At _least_ 1 space
            for (int k = 0; k < padding; k++)
               output.print(' ');
            output.print(s);
         }
         output.println();
      }
      output.println();   // end with blank line.
   }

   /** Read a matrix from a stream.  The format is the same the print method,
     * so printed matrices can be read back in (provided they were printed using
     * US Locale).  Elements are separated by
     * whitespace, all the elements for each row appear on a single line,
     * the last row is followed by a blank line.
   @param input the input stream.
   */

   public static Matrix read (BufferedReader input) throws java.io.IOException {
      StreamTokenizer tokenizer= new StreamTokenizer(input);

      // Although StreamTokenizer will parse numbers, it doesn't recognize
      // scientific notation (E or D); however, Double.valueOf does.
      // The strategy here is to disable StreamTokenizer's number parsing.
      // We'll only get whitespace delimited words, EOL's and EOF's.
      // These words should all be numbers, for Double.valueOf to parse.

      tokenizer.resetSyntax();
      tokenizer.wordChars(0,255);
      tokenizer.whitespaceChars(0, ' ');
      tokenizer.eolIsSignificant(true);
      java.util.Vector<Double> vD = new java.util.Vector<Double>();

      // Ignore initial empty lines
      while (tokenizer.nextToken() == StreamTokenizer.TT_EOL);
      if (tokenizer.ttype == StreamTokenizer.TT_EOF)
	throw new java.io.IOException("Unexpected EOF on matrix read.");
      do {
         vD.addElement(Double.valueOf(tokenizer.sval)); // Read & store 1st row.
      } while (tokenizer.nextToken() == StreamTokenizer.TT_WORD);

      int n = vD.size();  // Now we've got the number of columns!
      double row[] = new double[n];
      for (int j=0; j<n; j++)  // extract the elements of the 1st row.
         row[j]=vD.elementAt(j).doubleValue();
      java.util.Vector<double[]> v = new java.util.Vector<double[]>();
      v.addElement(row);  // Start storing rows instead of columns.
      while (tokenizer.nextToken() == StreamTokenizer.TT_WORD) {
         // While non-empty lines
         v.addElement(row = new double[n]);
         int j = 0;
         do {
            if (j >= n) throw new java.io.IOException
               ("Row " + v.size() + " is too long.");
            row[j++] = Double.valueOf(tokenizer.sval).doubleValue();
         } while (tokenizer.nextToken() == StreamTokenizer.TT_WORD);
         if (j < n) throw new java.io.IOException
            ("Row " + v.size() + " is too short.");
      }
      int m = v.size();  // Now we've got the number of rows.
      double[][] A = new double[m][];
      v.copyInto(A);  // copy the rows out of the vector
      return new Matrix(A);
   }


/* ------------------------
   Private Methods
 * ------------------------ */

   /** Check if size(A) == size(B) **/

   private void checkMatrixDimensions (Matrix B) {
      if (B.m != m || B.n != n) {
         throw new IllegalArgumentException("Matrix dimensions must agree.");
      }
   }

  private static final long serialVersionUID = 1;
}

3）原始碼參考EigenvalueDecomposition

可重點研讀如何實現特徵值分解。

package Jama;
import Jama.util.*;

/** Eigenvalues and eigenvectors of a real matrix. 
<P>
    If A is symmetric, then A = V*D*V' where the eigenvalue matrix D is
    diagonal and the eigenvector matrix V is orthogonal.
    I.e. A = V.times(D.times(V.transpose())) and 
    V.times(V.transpose()) equals the identity matrix.
<P>
    If A is not symmetric, then the eigenvalue matrix D is block diagonal
    with the real eigenvalues in 1-by-1 blocks and any complex eigenvalues,
    lambda + i*mu, in 2-by-2 blocks, [lambda, mu; -mu, lambda].  The
    columns of V represent the eigenvectors in the sense that A*V = V*D,
    i.e. A.times(V) equals V.times(D).  The matrix V may be badly
    conditioned, or even singular, so the validity of the equation
    A = V*D*inverse(V) depends upon V.cond().
**/

public class EigenvalueDecomposition implements java.io.Serializable {

/* ------------------------
   Class variables
 * ------------------------ */

   /** Row and column dimension (square matrix).
   @serial matrix dimension.
   */
   private int n;

   /** Symmetry flag.
   @serial internal symmetry flag.
   */
   private boolean issymmetric;

   /** Arrays for internal storage of eigenvalues.
   @serial internal storage of eigenvalues.
   */
   private double[] d, e;

   /** Array for internal storage of eigenvectors.
   @serial internal storage of eigenvectors.
   */
   private double[][] V;

   /** Array for internal storage of nonsymmetric Hessenberg form.
   @serial internal storage of nonsymmetric Hessenberg form.
   */
   private double[][] H;

   /** Working storage for nonsymmetric algorithm.
   @serial working storage for nonsymmetric algorithm.
   */
   private double[] ort;

/* ------------------------
   Private Methods
 * ------------------------ */

   // Symmetric Householder reduction to tridiagonal form.

   private void tred2 () {

   //  This is derived from the Algol procedures tred2 by
   //  Bowdler, Martin, Reinsch, and Wilkinson, Handbook for
   //  Auto. Comp., Vol.ii-Linear Algebra, and the corresponding
   //  Fortran subroutine in EISPACK.

      for (int j = 0; j < n; j++) {
         d[j] = V[n-1][j];
      }

      // Householder reduction to tridiagonal form.
   
      for (int i = n-1; i > 0; i--) {
   
         // Scale to avoid under/overflow.
   
         double scale = 0.0;
         double h = 0.0;
         for (int k = 0; k < i; k++) {
            scale = scale + Math.abs(d[k]);
         }
         if (scale == 0.0) {
            e[i] = d[i-1];
            for (int j = 0; j < i; j++) {
               d[j] = V[i-1][j];
               V[i][j] = 0.0;
               V[j][i] = 0.0;
            }
         } else {
   
            // Generate Householder vector.
   
            for (int k = 0; k < i; k++) {
               d[k] /= scale;
               h += d[k] * d[k];
            }
            double f = d[i-1];
            double g = Math.sqrt(h);
            if (f > 0) {
               g = -g;
            }
            e[i] = scale * g;
            h = h - f * g;
            d[i-1] = f - g;
            for (int j = 0; j < i; j++) {
               e[j] = 0.0;
            }
   
            // Apply similarity transformation to remaining columns.
   
            for (int j = 0; j < i; j++) {
               f = d[j];
               V[j][i] = f;
               g = e[j] + V[j][j] * f;
               for (int k = j+1; k <= i-1; k++) {
                  g += V[k][j] * d[k];
                  e[k] += V[k][j] * f;
               }
               e[j] = g;
            }
            f = 0.0;
            for (int j = 0; j < i; j++) {
               e[j] /= h;
               f += e[j] * d[j];
            }
            double hh = f / (h + h);
            for (int j = 0; j < i; j++) {
               e[j] -= hh * d[j];
            }
            for (int j = 0; j < i; j++) {
               f = d[j];
               g = e[j];
               for (int k = j; k <= i-1; k++) {
                  V[k][j] -= (f * e[k] + g * d[k]);
               }
               d[j] = V[i-1][j];
               V[i][j] = 0.0;
            }
         }
         d[i] = h;
      }
   
      // Accumulate transformations.
   
      for (int i = 0; i < n-1; i++) {
         V[n-1][i] = V[i][i];
         V[i][i] = 1.0;
         double h = d[i+1];
         if (h != 0.0) {
            for (int k = 0; k <= i; k++) {
               d[k] = V[k][i+1] / h;
            }
            for (int j = 0; j <= i; j++) {
               double g = 0.0;
               for (int k = 0; k <= i; k++) {
                  g += V[k][i+1] * V[k][j];
               }
               for (int k = 0; k <= i; k++) {
                  V[k][j] -= g * d[k];
               }
            }
         }
         for (int k = 0; k <= i; k++) {
            V[k][i+1] = 0.0;
         }
      }
      for (int j = 0; j < n; j++) {
         d[j] = V[n-1][j];
         V[n-1][j] = 0.0;
      }
      V[n-1][n-1] = 1.0;
      e[0] = 0.0;
   } 

   // Symmetric tridiagonal QL algorithm.
   
   private void tql2 () {

   //  This is derived from the Algol procedures tql2, by
   //  Bowdler, Martin, Reinsch, and Wilkinson, Handbook for
   //  Auto. Comp., Vol.ii-Linear Algebra, and the corresponding
   //  Fortran subroutine in EISPACK.
   
      for (int i = 1; i < n; i++) {
         e[i-1] = e[i];
      }
      e[n-1] = 0.0;
   
      double f = 0.0;
      double tst1 = 0.0;
      double eps = Math.pow(2.0,-52.0);
      for (int l = 0; l < n; l++) {

         // Find small subdiagonal element
   
         tst1 = Math.max(tst1,Math.abs(d[l]) + Math.abs(e[l]));
         int m = l;
         while (m < n) {
            if (Math.abs(e[m]) <= eps*tst1) {
               break;
            }
            m++;
         }
   
         // If m == l, d[l] is an eigenvalue,
         // otherwise, iterate.
   
         if (m > l) {
            int iter = 0;
            do {
               iter = iter + 1;  // (Could check iteration count here.)
   
               // Compute implicit shift
   
               double g = d[l];
               double p = (d[l+1] - g) / (2.0 * e[l]);
               double r = Maths.hypot(p,1.0);
               if (p < 0) {
                  r = -r;
               }
               d[l] = e[l] / (p + r);
               d[l+1] = e[l] * (p + r);
               double dl1 = d[l+1];
               double h = g - d[l];
               for (int i = l+2; i < n; i++) {
                  d[i] -= h;
               }
               f = f + h;
   
               // Implicit QL transformation.
   
               p = d[m];
               double c = 1.0;
               double c2 = c;
               double c3 = c;
               double el1 = e[l+1];
               double s = 0.0;
               double s2 = 0.0;
               for (int i = m-1; i >= l; i--) {
                  c3 = c2;
                  c2 = c;
                  s2 = s;
                  g = c * e[i];
                  h = c * p;
                  r = Maths.hypot(p,e[i]);
                  e[i+1] = s * r;
                  s = e[i] / r;
                  c = p / r;
                  p = c * d[i] - s * g;
                  d[i+1] = h + s * (c * g + s * d[i]);
   
                  // Accumulate transformation.
   
                  for (int k = 0; k < n; k++) {
                     h = V[k][i+1];
                     V[k][i+1] = s * V[k][i] + c * h;
                     V[k][i] = c * V[k][i] - s * h;
                  }
               }
               p = -s * s2 * c3 * el1 * e[l] / dl1;
               e[l] = s * p;
               d[l] = c * p;
   
               // Check for convergence.
   
            } while (Math.abs(e[l]) > eps*tst1);
         }
         d[l] = d[l] + f;
         e[l] = 0.0;
      }
     
      // Sort eigenvalues and corresponding vectors.
   
      for (int i = 0; i < n-1; i++) {
         int k = i;
         double p = d[i];
         for (int j = i+1; j < n; j++) {
            if (d[j] < p) {
               k = j;
               p = d[j];
            }
         }
         if (k != i) {
            d[k] = d[i];
            d[i] = p;
            for (int j = 0; j < n; j++) {
               p = V[j][i];
               V[j][i] = V[j][k];
               V[j][k] = p;
            }
         }
      }
   }

   // Nonsymmetric reduction to Hessenberg form.

   private void orthes () {
   
      //  This is derived from the Algol procedures orthes and ortran,
      //  by Martin and Wilkinson, Handbook for Auto. Comp.,
      //  Vol.ii-Linear Algebra, and the corresponding
      //  Fortran subroutines in EISPACK.
   
      int low = 0;
      int high = n-1;
   
      for (int m = low+1; m <= high-1; m++) {
   
         // Scale column.
   
         double scale = 0.0;
         for (int i = m; i <= high; i++) {
            scale = scale + Math.abs(H[i][m-1]);
         }
         if (scale != 0.0) {
   
            // Compute Householder transformation.
   
            double h = 0.0;
            for (int i = high; i >= m; i--) {
               ort[i] = H[i][m-1]/scale;
               h += ort[i] * ort[i];
            }
            double g = Math.sqrt(h);
            if (ort[m] > 0) {
               g = -g;
            }
            h = h - ort[m] * g;
            ort[m] = ort[m] - g;
   
            // Apply Householder similarity transformation
            // H = (I-u*u'/h)*H*(I-u*u')/h)
   
            for (int j = m; j < n; j++) {
               double f = 0.0;
               for (int i = high; i >= m; i--) {
                  f += ort[i]*H[i][j];
               }
               f = f/h;
               for (int i = m; i <= high; i++) {
                  H[i][j] -= f*ort[i];
               }
           }
   
           for (int i = 0; i <= high; i++) {
               double f = 0.0;
               for (int j = high; j >= m; j--) {
                  f += ort[j]*H[i][j];
               }
               f = f/h;
               for (int j = m; j <= high; j++) {
                  H[i][j] -= f*ort[j];
               }
            }
            ort[m] = scale*ort[m];
            H[m][m-1] = scale*g;
         }
      }
   
      // Accumulate transformations (Algol's ortran).

      for (int i = 0; i < n; i++) {
         for (int j = 0; j < n; j++) {
            V[i][j] = (i == j ? 1.0 : 0.0);
         }
      }

      for (int m = high-1; m >= low+1; m--) {
         if (H[m][m-1] != 0.0) {
            for (int i = m+1; i <= high; i++) {
               ort[i] = H[i][m-1];
            }
            for (int j = m; j <= high; j++) {
               double g = 0.0;
               for (int i = m; i <= high; i++) {
                  g += ort[i] * V[i][j];
               }
               // Double division avoids possible underflow
               g = (g / ort[m]) / H[m][m-1];
               for (int i = m; i <= high; i++) {
                  V[i][j] += g * ort[i];
               }
            }
         }
      }
   }


   // Complex scalar division.

   private transient double cdivr, cdivi;
   private void cdiv(double xr, double xi, double yr, double yi) {
      double r,d;
      if (Math.abs(yr) > Math.abs(yi)) {
         r = yi/yr;
         d = yr + r*yi;
         cdivr = (xr + r*xi)/d;
         cdivi = (xi - r*xr)/d;
      } else {
         r = yr/yi;
         d = yi + r*yr;
         cdivr = (r*xr + xi)/d;
         cdivi = (r*xi - xr)/d;
      }
   }


   // Nonsymmetric reduction from Hessenberg to real Schur form.

   private void hqr2 () {
   
      //  This is derived from the Algol procedure hqr2,
      //  by Martin and Wilkinson, Handbook for Auto. Comp.,
      //  Vol.ii-Linear Algebra, and the corresponding
      //  Fortran subroutine in EISPACK.
   
      // Initialize
   
      int nn = this.n;
      int n = nn-1;
      int low = 0;
      int high = nn-1;
      double eps = Math.pow(2.0,-52.0);
      double exshift = 0.0;
      double p=0,q=0,r=0,s=0,z=0,t,w,x,y;
   
      // Store roots isolated by balanc and compute matrix norm
   
      double norm = 0.0;
      for (int i = 0; i < nn; i++) {
         if (i < low | i > high) {
            d[i] = H[i][i];
            e[i] = 0.0;
         }
         for (int j = Math.max(i-1,0); j < nn; j++) {
            norm = norm + Math.abs(H[i][j]);
         }
      }
   
      // Outer loop over eigenvalue index
   
      int iter = 0;
      while (n >= low) {
   
         // Look for single small sub-diagonal element
   
         int l = n;
         while (l > low) {
            s = Math.abs(H[l-1][l-1]) + Math.abs(H[l][l]);
            if (s == 0.0) {
               s = norm;
            }
            if (Math.abs(H[l][l-1]) < eps * s) {
               break;
            }
            l--;
         }
       
         // Check for convergence
         // One root found
   
         if (l == n) {
            H[n][n] = H[n][n] + exshift;
            d[n] = H[n][n];
            e[n] = 0.0;
            n--;
            iter = 0;
   
         // Two roots found
   
         } else if (l == n-1) {
            w = H[n][n-1] * H[n-1][n];
            p = (H[n-1][n-1] - H[n][n]) / 2.0;
            q = p * p + w;
            z = Math.sqrt(Math.abs(q));
            H[n][n] = H[n][n] + exshift;
            H[n-1][n-1] = H[n-1][n-1] + exshift;
            x = H[n][n];
   
            // Real pair
   
            if (q >= 0) {
               if (p >= 0) {
                  z = p + z;
               } else {
                  z = p - z;
               }
               d[n-1] = x + z;
               d[n] = d[n-1];
               if (z != 0.0) {
                  d[n] = x - w / z;
               }
               e[n-1] = 0.0;
               e[n] = 0.0;
               x = H[n][n-1];
               s = Math.abs(x) + Math.abs(z);
               p = x / s;
               q = z / s;
               r = Math.sqrt(p * p+q * q);
               p = p / r;
               q = q / r;
   
               // Row modification
   
               for (int j = n-1; j < nn; j++) {
                  z = H[n-1][j];
                  H[n-1][j] = q * z + p * H[n][j];
                  H[n][j] = q * H[n][j] - p * z;
               }
   
               // Column modification
   
               for (int i = 0; i <= n; i++) {
                  z = H[i][n-1];
                  H[i][n-1] = q * z + p * H[i][n];
                  H[i][n] = q * H[i][n] - p * z;
               }
   
               // Accumulate transformations
   
               for (int i = low; i <= high; i++) {
                  z = V[i][n-1];
                  V[i][n-1] = q * z + p * V[i][n];
                  V[i][n] = q * V[i][n] - p * z;
               }
   
            // Complex pair
   
            } else {
               d[n-1] = x + p;
               d[n] = x + p;
               e[n-1] = z;
               e[n] = -z;
            }
            n = n - 2;
            iter = 0;
   
         // No convergence yet
   
         } else {
   
            // Form shift
   
            x = H[n][n];
            y = 0.0;
            w = 0.0;
            if (l < n) {
               y = H[n-1][n-1];
               w = H[n][n-1] * H[n-1][n];
            }
   
            // Wilkinson's original ad hoc shift
   
            if (iter == 10) {
               exshift += x;
               for (int i = low; i <= n; i++) {
                  H[i][i] -= x;
               }
               s = Math.abs(H[n][n-1]) + Math.abs(H[n-1][n-2]);
               x = y = 0.75 * s;
               w = -0.4375 * s * s;
            }

            // MATLAB's new ad hoc shift

            if (iter == 30) {
                s = (y - x) / 2.0;
                s = s * s + w;
                if (s > 0) {
                    s = Math.sqrt(s);
                    if (y < x) {
                       s = -s;
                    }
                    s = x - w / ((y - x) / 2.0 + s);
                    for (int i = low; i <= n; i++) {
                       H[i][i] -= s;
                    }
                    exshift += s;
                    x = y = w = 0.964;
                }
            }
   
            iter = iter + 1;   // (Could check iteration count here.)
   
            // Look for two consecutive small sub-diagonal elements
   
            int m = n-2;
            while (m >= l) {
               z = H[m][m];
               r = x - z;
               s = y - z;
               p = (r * s - w) / H[m+1][m] + H[m][m+1];
               q = H[m+1][m+1] - z - r - s;
               r = H[m+2][m+1];
               s = Math.abs(p) + Math.abs(q) + Math.abs(r);
               p = p / s;
               q = q / s;
               r = r / s;
               if (m == l) {
                  break;
               }
               if (Math.abs(H[m][m-1]) * (Math.abs(q) + Math.abs(r)) <
                  eps * (Math.abs(p) * (Math.abs(H[m-1][m-1]) + Math.abs(z) +
                  Math.abs(H[m+1][m+1])))) {
                     break;
               }
               m--;
            }
   
            for (int i = m+2; i <= n; i++) {
               H[i][i-2] = 0.0;
               if (i > m+2) {
                  H[i][i-3] = 0.0;
               }
            }
   
            // Double QR step involving rows l:n and columns m:n
   

            for (int k = m; k <= n-1; k++) {
               boolean notlast = (k != n-1);
               if (k != m) {
                  p = H[k][k-1];
                  q = H[k+1][k-1];
                  r = (notlast ? H[k+2][k-1] : 0.0);
                  x = Math.abs(p) + Math.abs(q) + Math.abs(r);
                  if (x == 0.0) {
                      continue;
                  }
                  p = p / x;
                  q = q / x;
                  r = r / x;
               }

               s = Math.sqrt(p * p + q * q + r * r);
               if (p < 0) {
                  s = -s;
               }
               if (s != 0) {
                  if (k != m) {
                     H[k][k-1] = -s * x;
                  } else if (l != m) {
                     H[k][k-1] = -H[k][k-1];
                  }
                  p = p + s;
                  x = p / s;
                  y = q / s;
                  z = r / s;
                  q = q / p;
                  r = r / p;
   
                  // Row modification
   
                  for (int j = k; j < nn; j++) {
                     p = H[k][j] + q * H[k+1][j];
                     if (notlast) {
                        p = p + r * H[k+2][j];
                        H[k+2][j] = H[k+2][j] - p * z;
                     }
                     H[k][j] = H[k][j] - p * x;
                     H[k+1][j] = H[k+1][j] - p * y;
                  }
   
                  // Column modification
   
                  for (int i = 0; i <= Math.min(n,k+3); i++) {
                     p = x * H[i][k] + y * H[i][k+1];
                     if (notlast) {
                        p = p + z * H[i][k+2];
                        H[i][k+2] = H[i][k+2] - p * r;
                     }
                     H[i][k] = H[i][k] - p;
                     H[i][k+1] = H[i][k+1] - p * q;
                  }
   
                  // Accumulate transformations
   
                  for (int i = low; i <= high; i++) {
                     p = x * V[i][k] + y * V[i][k+1];
                     if (notlast) {
                        p = p + z * V[i][k+2];
                        V[i][k+2] = V[i][k+2] - p * r;
                     }
                     V[i][k] = V[i][k] - p;
                     V[i][k+1] = V[i][k+1] - p * q;
                  }
               }  // (s != 0)
            }  // k loop
         }  // check convergence
      }  // while (n >= low)
      
      // Backsubstitute to find vectors of upper triangular form

      if (norm == 0.0) {
         return;
      }
   
      for (n = nn-1; n >= 0; n--) {
         p = d[n];
         q = e[n];
   
         // Real vector
   
         if (q == 0) {
            int l = n;
            H[n][n] = 1.0;
            for (int i = n-1; i >= 0; i--) {
               w = H[i][i] - p;
               r = 0.0;
               for (int j = l; j <= n; j++) {
                  r = r + H[i][j] * H[j][n];
               }
               if (e[i] < 0.0) {
                  z = w;
                  s = r;
               } else {
                  l = i;
                  if (e[i] == 0.0) {
                     if (w != 0.0) {
                        H[i][n] = -r / w;
                     } else {
                        H[i][n] = -r / (eps * norm);
                     }
   
                  // Solve real equations
   
                  } else {
                     x = H[i][i+1];
                     y = H[i+1][i];
                     q = (d[i] - p) * (d[i] - p) + e[i] * e[i];
                     t = (x * s - z * r) / q;
                     H[i][n] = t;
                     if (Math.abs(x) > Math.abs(z)) {
                        H[i+1][n] = (-r - w * t) / x;
                     } else {
                        H[i+1][n] = (-s - y * t) / z;
                     }
                  }
   
                  // Overflow control
   
                  t = Math.abs(H[i][n]);
                  if ((eps * t) * t > 1) {
                     for (int j = i; j <= n; j++) {
                        H[j][n] = H[j][n] / t;
                     }
                  }
               }
            }
   
         // Complex vector
   
         } else if (q < 0) {
            int l = n-1;

            // Last vector component imaginary so matrix is triangular
   
            if (Math.abs(H[n][n-1]) > Math.abs(H[n-1][n])) {
               H[n-1][n-1] = q / H[n][n-1];
               H[n-1][n] = -(H[n][n] - p) / H[n][n-1];
            } else {
               cdiv(0.0,-H[n-1][n],H[n-1][n-1]-p,q);
               H[n-1][n-1] = cdivr;
               H[n-1][n] = cdivi;
            }
            H[n][n-1] = 0.0;
            H[n][n] = 1.0;
            for (int i = n-2; i >= 0; i--) {
               double ra,sa,vr,vi;
               ra = 0.0;
               sa = 0.0;
               for (int j = l; j <= n; j++) {
                  ra = ra + H[i][j] * H[j][n-1];
                  sa = sa + H[i][j] * H[j][n];
               }
               w = H[i][i] - p;
   
               if (e[i] < 0.0) {
                  z = w;
                  r = ra;
                  s = sa;
               } else {
                  l = i;
                  if (e[i] == 0) {
                     cdiv(-ra,-sa,w,q);
                     H[i][n-1] = cdivr;
                     H[i][n] = cdivi;
                  } else {
   
                     // Solve complex equations
   
                     x = H[i][i+1];
                     y = H[i+1][i];
                     vr = (d[i] - p) * (d[i] - p) + e[i] * e[i] - q * q;
                     vi = (d[i] - p) * 2.0 * q;
                     if (vr == 0.0 & vi == 0.0) {
                        vr = eps * norm * (Math.abs(w) + Math.abs(q) +
                        Math.abs(x) + Math.abs(y) + Math.abs(z));
                     }
                     cdiv(x*r-z*ra+q*sa,x*s-z*sa-q*ra,vr,vi);
                     H[i][n-1] = cdivr;
                     H[i][n] = cdivi;
                     if (Math.abs(x) > (Math.abs(z) + Math.abs(q))) {
                        H[i+1][n-1] = (-ra - w * H[i][n-1] + q * H[i][n]) / x;
                        H[i+1][n] = (-sa - w * H[i][n] - q * H[i][n-1]) / x;
                     } else {
                        cdiv(-r-y*H[i][n-1],-s-y*H[i][n],z,q);
                        H[i+1][n-1] = cdivr;
                        H[i+1][n] = cdivi;
                     }
                  }
   
                  // Overflow control

                  t = Math.max(Math.abs(H[i][n-1]),Math.abs(H[i][n]));
                  if ((eps * t) * t > 1) {
                     for (int j = i; j <= n; j++) {
                        H[j][n-1] = H[j][n-1] / t;
                        H[j][n] = H[j][n] / t;
                     }
                  }
               }
            }
         }
      }
   
      // Vectors of isolated roots
   
      for (int i = 0; i < nn; i++) {
         if (i < low | i > high) {
            for (int j = i; j < nn; j++) {
               V[i][j] = H[i][j];
            }
         }
      }
   
      // Back transformation to get eigenvectors of original matrix
   
      for (int j = nn-1; j >= low; j--) {
         for (int i = low; i <= high; i++) {
            z = 0.0;
            for (int k = low; k <= Math.min(j,high); k++) {
               z = z + V[i][k] * H[k][j];
            }
            V[i][j] = z;
         }
      }
   }


/* ------------------------
   Constructor
 * ------------------------ */

   /** Check for symmetry, then construct the eigenvalue decomposition
       Structure to access D and V.
   @param Arg    Square matrix
   */

   public EigenvalueDecomposition (Matrix Arg) {
      double[][] A = Arg.getArray();
      n = Arg.getColumnDimension();
      V = new double[n][n];
      d = new double[n];
      e = new double[n];

      issymmetric = true;
      for (int j = 0; (j < n) & issymmetric; j++) {
         for (int i = 0; (i < n) & issymmetric; i++) {
            issymmetric = (A[i][j] == A[j][i]);
         }
      }

      if (issymmetric) {
         for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
               V[i][j] = A[i][j];
            }
         }
   
         // Tridiagonalize.
         tred2();
   
         // Diagonalize.
         tql2();

      } else {
         H = new double[n][n];
         ort = new double[n];
         
         for (int j = 0; j < n; j++) {
            for (int i = 0; i < n; i++) {
               H[i][j] = A[i][j];
            }
         }
   
         // Reduce to Hessenberg form.
         orthes();
   
         // Reduce Hessenberg to real Schur form.
         hqr2();
      }
   }

/* ------------------------
   Public Methods
 * ------------------------ */

   /** Return the eigenvector matrix
   @return     V
   */

   public Matrix getV () {
      return new Matrix(V,n,n);
   }

   /** Return the real parts of the eigenvalues
   @return     real(diag(D))
   */

   public double[] getRealEigenvalues () {
      return d;
   }

   /** Return the imaginary parts of the eigenvalues
   @return     imag(diag(D))
   */

   public double[] getImagEigenvalues () {
      return e;
   }

   /** Return the block diagonal eigenvalue matrix
   @return     D
   */

   public Matrix getD () {
      Matrix X = new Matrix(n,n);
      double[][] D = X.getArray();
      for (int i = 0; i < n; i++) {
         for (int j = 0; j < n; j++) {
            D[i][j] = 0.0;
         }
         D[i][i] = d[i];
         if (e[i] > 0) {
            D[i][i+1] = e[i];
         } else if (e[i] < 0) {
            D[i][i-1] = e[i];
         }
      }
      return X;
   }
  private static final long serialVersionUID = 1;
}


相關推薦

機器學習知識點(十九)矩陣特徵值分解基礎知識及Java實現

1、特徵值分解基礎知識 矩陣乘法Y=AB的數學意義在於變換，以其中一個向量A為中心，則B的作用主要是使A發生伸縮或旋轉變換。一個矩陣其實就是一個線性變換，因為一個矩陣乘以一個向量後得到的向量，其實就相當於將這個向量進行了線性變換。 如果說一個向量v是方陣A的特徵向量，將一定

機器學習知識點(十六)整合學習AdaBoost演算法Java實現

理解http://blog.csdn.net/fjssharpsword/article/details/61913092中AdaBoost演算法，從網上找了一套簡單的程式碼加以理解。 1、基分類器，實現一個簡單的分類 1）物件類 package sk.adaboost;

機器學習（十九）——拉普拉斯光順（Laplace smoothing）

我們已經描述過的樸素貝葉斯演算法能夠很好地解決許多問題，但是有一個簡單的改變使得它更好地工作，特別是對於文字分類。讓我們簡單地討論演算法在當前形式下的問題，然後討論如何修復它。考慮垃圾郵件/電子郵件分類，讓我們假設在完成CS229並完成了對專案的出色工作之後，您決定在2003

機器學習（十九）——PageRank演算法, KNN, loss function詳解

PageRank演算法 概述 在PageRank提出之前，已經有研究者提出利用網頁的入鏈數量來進行連結分析計算，這種入鏈方法假設一個網頁的入鏈越多，則該網頁越重要。早期的很多搜尋引擎也採納了入鏈數量作為連結分析方法，對於搜尋引擎效果提升也有較明顯

《機器學習實戰》支援向量機的數學理解及程式實現

一、 引言最近在機器學習課上，學到的《機器學習實戰》第六章的支援向量機，這部分內容非常多，不僅要會程式設計和測試，還要理解它的數學基礎，這裡對這部分的學習進行一些總結。二、 SVM的數學原理從一個簡單的二分問題開始說吧：我們要把這兩類不同的點區分開，那麼在這個二維平面上就是找

機器學習（十二）——機器學習中的矩陣方法（2）特徵值和奇異值

QR分解（續） 令A=[a1,⋯,an]，其中ai為列向量。則： u1u2u3uk=a1,=a2−proju1a2,=a3−proju1a3−proju2a3,⋮=ak−∑j=1k−1projujak,e1e2e3ek=u1∥u1∥=u2∥u2∥=u3∥

機器學習之python學習（十九）

今天來學習python中的檔案操作這是很關鍵的， 這次先學習檔案的讀寫，需要注意的是檔案的許可權的問題。 總結如下最常用的許可權： 許可權 數量 r 開啟只讀檔案，該檔案必須存在。

機器學習與深度學習系列連載： 第二部分 深度學習（十九) 注意力機制 Attention

注意力機制 Attention 我們以機器翻譯為例，來探究引入注意力機制Attention： 當我們使用Seq2Seq 進行機器翻譯的過程中，最後的輸入對結果影響響度比較大，因為Encode的輸出是在尾部（圖中粉紅色部分）。直覺上想，一段話的翻譯的的過程中，輸

Tensorflow深度學習之十九：矩陣切片與連結

1、TensorFlow矩陣切片操作：tf.slice函式 函式原型：slice(input_, begin, size, name=None) 引數： input：待切片的矩陣tensor。 begin：起始位置，表示從哪一個資料開始進行切片。這個起始

JAVA學習第十九課（java程序的異常處理 （二））

num 函數 錯誤 style col 編譯失敗 return [] java 異常處理的捕捉形式： 這是能夠對異常進行針對性處理的方式 六、try、catch的理解 詳細格式： try { //須要被檢測異常的代碼 } catch（異常類 變量）//改變量用

開發者成功使用機器學習的十大訣竅

mdm tk1 dex oda nco mdi 開發 mda jmx bbossgencodev5036%E5%8F%91%E5%B8%83%E4%BB%A3%E7%A0%81%E7%94%9F%E6%88%90%E5%B7%A5%E5%85%B7 http://www.

學習二十九

linux學習七周三次課（3月21日）10.11 Linux網絡相關10.12 firewalld和netfilter10.13 netfilter5表5鏈介紹10.14 iptables語法 擴展（selinux了解即可） selinux教程 http://os.51cto.com/art/201209

機器學習知識點查漏補缺（隨機森林和extraTrees）

efault 生成 xtra lac use sample strategy default lin 隨機森林 對數據樣本及特征隨機抽取，進行多個決策樹訓練，防止過擬合，提高泛化能力 一般隨機森林的特點： 1、有放回抽樣（所以生成每棵樹的時候，實際數據集會有重復），

機器學習知識點查漏補缺（支持向量機）

技巧 條件 blog 更多 nbsp pos .com 最優化 應該 一、模型概念 支持向量機的模型基本模型是建立在特征空間上的最大間隔線性分類器，通過使用核技巧，可以使它成為非線性分類器。 當訓練數據線性可分時，通過硬間隔最大化，學習一個線性分類器，即線性可分支持向量

機器學習知識點查漏補缺（樸素貝葉斯分類）

平滑 http 運算 貝葉斯公式 -s 目標 bubuko 思想 指數 一、基本模型 樸素貝葉斯分類模型的基本思想就是貝葉斯公式，對以特征為條件的各類別的後驗概率。 貝葉斯公式如下： 對標樸素貝葉斯分類模型的公式如下： 分子中的第二項為每個類別的概率（實際運算即頻

學習四十九

linux學習13.1 設置更改root密碼13.2 連接mysql13.3 mysql常用命令擴展 mysql5.7 root密碼更改 http://www.apelearn.com/bbs/thread-7289-1-1.htmlmyisam 和innodb引擎對比 http://www.purewebe

學習五十九

linux學習5月23日任務18.11 LVS DR模式搭建18.12 keepalived + LVS 擴展haproxy+keepalived http://blog.csdn.net/xrt95050/article/details/40926255nginx、lvs、haproxy比較 http://

機器學習知識點01-監督學習

結果 you 組成 都是 直線擬合 表示 idt 選擇 分類問題 從這篇隨筆開始是觀看斯坦福大學（吳恩達）機器學習課程，個人覺得課程講的非常棒，也很容易理解，特此總結知識點筆記。筆記如下： 我們應用學習算法，可以在這

C++語言學習（十九）——C++類型識別

c++類 面向 字節 檢查 case include 指向 指針和引用 peid C++語言學習（十九）——C++類型識別 一、C++類型識別簡介 1、C++類型識別簡介 C++是靜態類型語言，其數據類型是在編譯期就確定的，不能在運行時更改。C++語言中，靜態類型是對象自身

GO語言學習（十九）Go 錯誤處理

錯誤處理 math println 接口 class int 處理機 nil sprintf Go 錯誤處理 Go 語言通過內置的錯誤接口提供了非常簡單的錯誤處理機制。 error類型是一個接口類型，這是它的定義： type error interface {