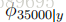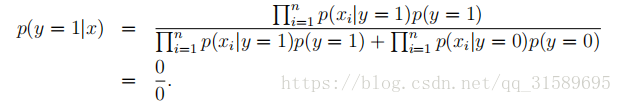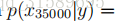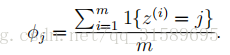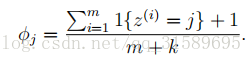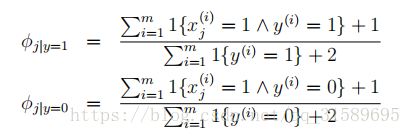我們已經描述過的樸素貝葉斯演算法能夠很好地解決許多問題，但是有一個簡單的改變使得它更好地工作，特別是對於文字分類。讓我們簡單地討論演算法在當前形式下的問題，然後討論如何修復它。

考慮垃圾郵件/電子郵件分類，讓我們假設在完成CS229並完成了對專案的出色工作之後，您決定在2003年6月左右將您所做的工作提交給NIPS會議以供發表。因為您在電子郵件中最終討論了會議，因此您還可以開始使用其中的“NIPS”一詞來獲取訊息。但這是你的第一份 NIPS 郵件，在此之前，你還沒有見過任何包含“nips”這個詞的電子郵件；特別是，“nips”從來沒有出現在你的培訓集的垃圾郵件/非垃圾郵件。假設“nips”是字典中的第35000個單詞，那麼您的樸素貝葉斯垃圾郵件過濾器就選擇了引數

也就是說，因為它以前從未在垃圾郵件或非垃圾郵件培訓示例中見過“nips”，它認為在兩種型別的電子郵件中看到“nips”的概率都是零。因此，當試圖確定其中一個包含“nips”的訊息是否是垃圾郵件時，它會計算類後驗概率，並獲得

這是因為每一個術語都包含一個項，並乘以它。因此，我們的演算法得到0/0，而且不知道如何進行預測。

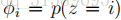
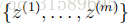
更廣泛地說明這個問題，從統計學上來說，估計某個事件的概率為零是個壞主意，僅僅因為你以前還沒有在有限的訓練集中看到過它。取{1，…，k}中取值的多項式隨機變數z的均值問題。我們可以用引數化我們的多項式。給定一組m個獨立觀測，給出了最大似然估計

正如我們之前看到的，如果我們使用這些最大似然估計，那麼一些

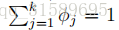
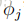
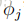
在這裡，我們把1加到分子上，把k加到分母上。注意，仍然有效(請自己檢查這一點！)，這是一個理想的性質，因為是我們所知道的概率的估計，我們知道的概率之和必須是1。另外，對於j的所有值，，解決了我們的概率估計為零的問題。在某些（相當強的）條件下，可以證明拉普拉斯平滑實際上給出了的最優估計量。

返回到我們的樸素貝葉斯分類器，通過拉普拉斯光順，我們得到了以下引數的估計：

(在實踐中，我們是否將laplace光順應用於並不太重要，因為我們通常會有相當比例的垃圾郵件和非垃圾郵件，所以是p(y=1)的合理的估計，將無論如何離0都會很遠。）