1. 題目簡介

Input: n points in the plane p1,p2,⋯,pn, where pi=(xi,yi)

Output: 包含所有點的最小凸多邊形的所有邊

2. 基本思想 ：Divide and Conquer

先把點集一分為二，分別求取相應凸多邊形，然後對兩個凸多邊形合併。

3. 具體演算法

1. sort P={pi} for i=1⋯n, such that x1<x2<⋯xn
2. divide P into PL and PR equally by picking the median of X, xmedian. Then PL={pi} iff. x
   i<xmedian, and PR=P−PL
3. After division, do it recursively.
4. Merge: that’s the difficult part and we will expand it in detail.

4. 融合兩個凸多邊形

這部分是對具體演算法第四部分的展開。
輸入是兩個點集以及包含相應點集的最小凸多邊形，且有兩個點集的X域不交叉，求一個O(N)的融合演算法。

討論包含所有點的最小凸多邊形的性質。筆者能夠想到的最簡單的方法就是列舉任意三個點，然後對所有三個點所構成的三角形取並集。
但這個演算法明顯是O(N！)的。如果能夠找到一個比較好的切入點，就會大幅降低了演算法複雜度。

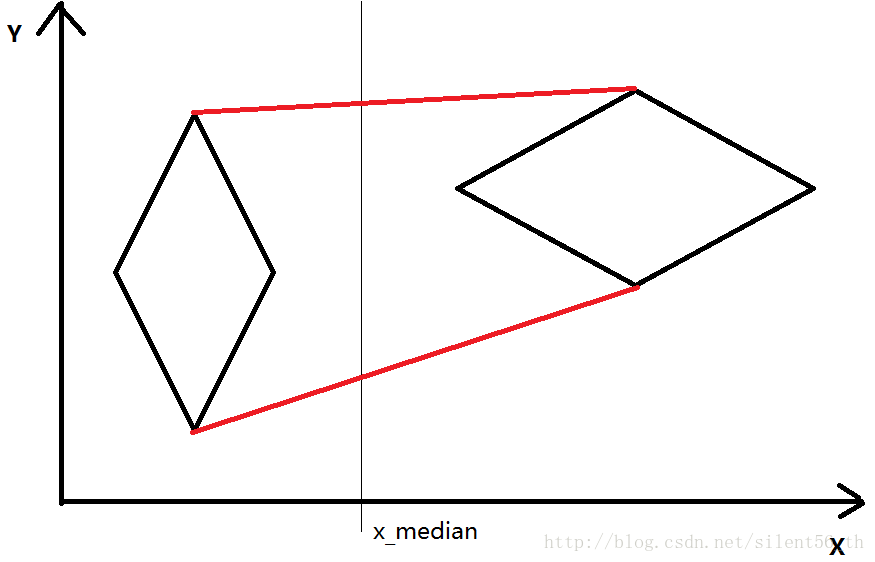
如下圖所示，黑色菱形為已經計算好的兩個凸多邊形。對兩者進行融合，其實是去尋找合理的兩條紅邊，只需要討論紅邊應該具有什麼性質即可。

這個性質很直接了，凸多邊形應該包含點集裡面的所有點，並且因為是凸多邊形，即所有角度數小於180°。
綜上所述，對於上面的紅邊，應該有點集裡面的所有點都比紅邊低，否則比紅邊高的點將不會被包含在以紅邊為邊的所有凸多邊形內。
形式化上訴結論有：

得到紅邊之後，逐一比較xi∗a+b和yi，若兩者相等，則該點為凸多邊形的頂點。

5. 整體演算法的時間複雜度

如上所訴，有T(N)=T(N/2)+O(N)，容易求解T(N)=O(NlogN)。

6. 演算法複雜性與資料性質的關係

1. 若N極大，則複雜性為O(1)。

   證明：因為推廣N到inf，則覆蓋全域，凸多邊形為包含全域的凸多邊形。

2. 若已知最終的凸多邊形的邊數一定，為h。則複雜性最終為O(Nlogh)。

   證明：將求解凸多邊形問題轉換為求解凸多邊形所有邊的問題，進而可以將其轉換為求解凸多邊形上邊和下邊的問題。

   易證凸多邊形的頂點中必然存在(x1,y1)和(xN,yN)，其中x1=min(x),xN=max(x)。 然後對凸多邊形的邊根據pmin和pmax進行劃分，分為上邊集和下邊集，上邊集和下邊集交集為NULL，並集為所有邊，上邊位於所有下邊上方。如下圖所示，紅邊為上邊，黑邊為下邊。

​ 上邊和下邊的數目最多為h，現計算求解上邊集的演算法複雜性。

​ T(N,h)=T(N/2,h1)+T(N/2,h2)+O(N)，其中h=h1+h2+1。

​ 假設T(N,h)=O(Nlogh)，使用歸納法即可驗證。