綜述：

使用遞迴求解問題有時往往令人費解，博主對遞迴也是頭痛不已，以下問題，利用遞迴很容易求解。總的來說，遞迴需要設計成：處理單個問題，遞迴求解子問題，設定出口。需要銘記的是遞迴所做的工作和處理單個問題一樣，所以只要單個問題取遍所有情況，那麼遞迴同樣也能取得所有情況。切記不要去想遞迴到底怎麼一層層的呼叫，不管是讀程式碼還是寫程式碼，需要關注的是遞迴出口，程式怎麼設計求解單個問題，一旦單個問題解決了，後續子問題就和解決單個問題一樣。

輸入：[1,2,3]

輸出：[[3],[1],[2],[1,2,3],[1,3],[2,3],[1,2],[]]

這個題目如何設計遞迴？我們可以把輸入資料分為第一個元素和剩下的元素（這樣分析正符合遞迴的思想），那麼輸入的子集中只有兩種情況：

1.包含第一個元素

2.不包含第一個元素

對應著程式就是取第一個元素，不取第一個元素。那麼程式該如何設計？

我們可以想象：

取第一個元素，相當於將第一個元素加入到後續遞迴的問題中，即後續遞迴解中一定包含第一個元素；

不取第一個元素，那其實更簡單，只需要遞迴求解剩下的所有元素，即略過第一個元素。

那麼我們這樣就已經取遍所有情況了嗎？我說是的，讀者不明白可以再多思考一下。別人講明白和自己想明白完全不是一回事，後者往往更重要。

這裡直接貼出Leetcode中的遞迴方案，並加以解釋：

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        //這裡排序並不必須，只是為了子集中元素以遞增排序
        sort(nums.begin(), nums.end());
        vector<vector<int>> subs;
        vector<int> sub;  
        genSubsets(nums, 0, sub, subs);
        return subs; 
    }
    void genSubsets(vector<int>& nums, int start, vector<int>& sub, vector<vector<int>>& subs) {
        //我們發現這裡好像並沒有遞迴出口，因為終止條件由下面for迴圈控制
        subs.push_back(sub);        
        for (int i = start; i < nums.size(); i++) {
            //情況一：子集包含元素nums[i]
            sub.push_back(nums[i]);
            //為何是i+1,因為已經解決了第i個元素，需要遞迴從第i+1個元素開始求解
            genSubsets(nums, i + 1, sub, subs);
            //情況二:子集不包含nums[i]，即略過第i個元素
            //可以想象，不去管上一條遞迴語句，當下一次迴圈到i+1時，第i個元素已經略過
            sub.pop_back();
        }
    }
};
 

輸入：[1,2,2]

輸出：[[1],[2],[1,2,2],[2,2],[1,2],[]]

這和上面的問題只多了重複的元素，在上面for迴圈的開始加上一句：

if(i > start && nums[i] == nums[i-1]) continue;

並且，對輸入陣列先排序，這裡就是必須的了，為何加上這個就能避免重複？一定要特別關注i>start,這說明了如果去重，必須第i-1個元素也在當前迴圈中，意思是for迴圈已經處理完第i-1個元素了，這時for迴圈裡對i-1的遞迴也結束了，最後一條語句sub.pop_back()也執行完了，現在for迴圈要處理第i個元素了。那這時為什麼要略過第i個元素呢？舉個例子，因為start<=i-1，我們關注從start開始的迴圈，那麼當迴圈到第i-1個元素結束時，子集中一定包含{nums[start],……，nums[i-1]}，現在請注意，迴圈第i-1個元素結束時，第i-1個元素已經彈出，下一次迴圈到第i個元素時，如果nums[i]==nums[i-1]我們不略過第i元素，那麼必定會產生{nums[start],……，nums[i]}，這裡面一定不包括nums[i-1](已經彈出)，這樣就產生了重複。

讀者可能會問，那麼像{1,2,2}這種時怎麼產生的呢？這個問題留給讀者自己思考。

輸入：[1,2,2]

輸出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

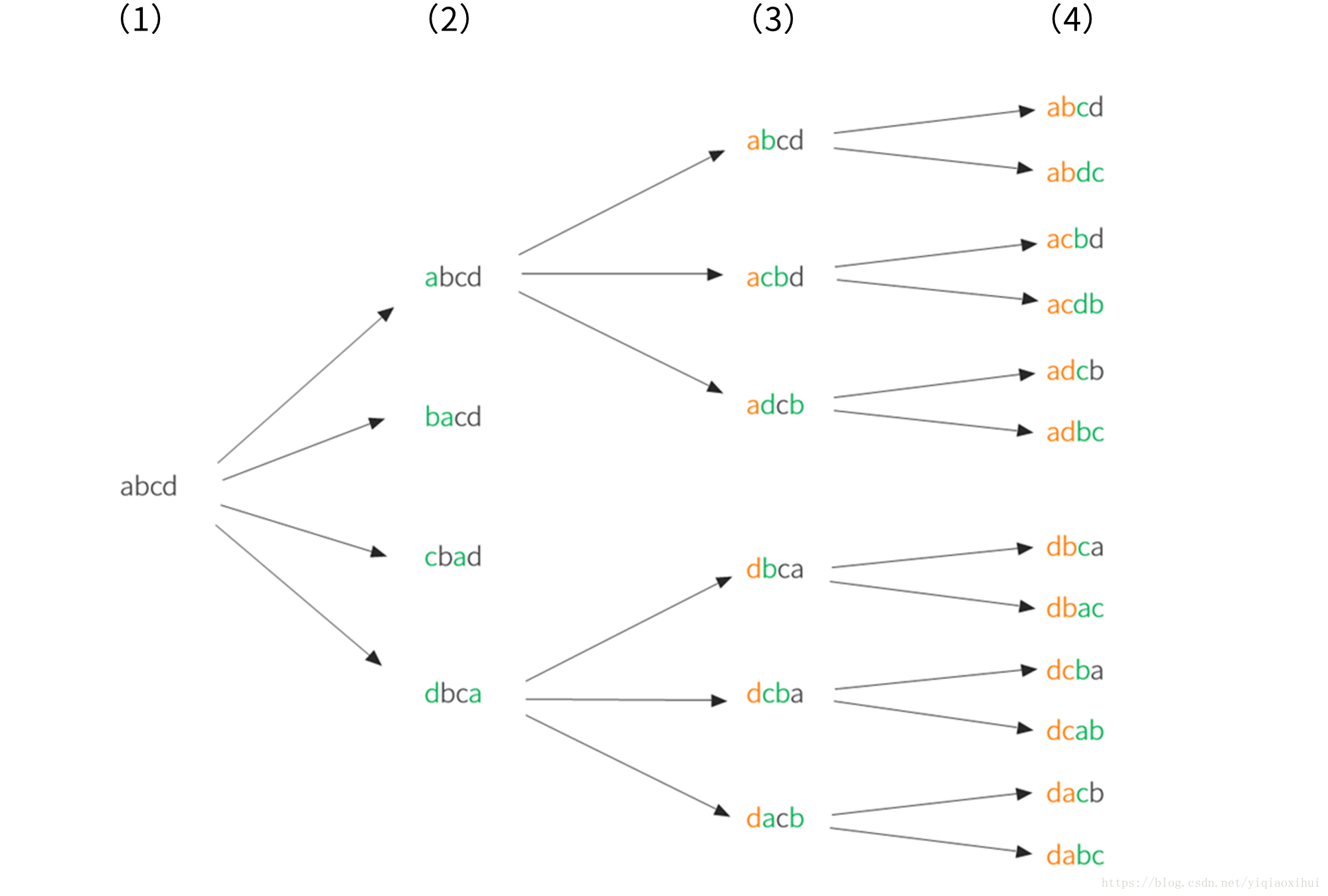
這是一個非常典型的遞迴問題，關鍵是如何將它轉化為一個遞迴問題。對於單個問題，如何能夠取得它的每一種情況？只有在單個問題中考慮所有的情況，自然遞迴子問題也能取遍所有情況。借圖說明問題

我們還可以將輸入陣列看成兩部分，就是第一個元素和剩餘元素，我經常強調這樣考慮問題的重要性。看出解決這個問題分兩步：

1.對於排列，與其說第一個元素，倒不如說第一個位置。第一步就是在第一個位置取遍所有的元素

2.第二步就是按照第一步處理方式遞迴求解剩下的元素。

怎樣才能在第一個位置取遍所有元素？我們可以將第一個元素每一次都和後面的元素交換位置，那麼第一個位置就取遍了所有的元素（對應圖片中的（1）->（2）），既然第一個位置所有解都已經解決，我們就求解剩下的位置，即遞迴求解和第一個元素交換後的剩下的元素，處理方式當然和處理第一個元素一樣。第一個元素和後面元素每次交換後，每次後面的元素不可能相同，因此不用考慮遞迴時會出現重複的情況。結合下面程式碼，可能更好理解。

class Solution{
public:
	vector<vector<int>> permute(vector<int>& nums) {
		//sort(nums.begin(), nums.end());
		vector<vector<int>> subs;
		vector<int> sub;
		genSubsets(nums, 0, subs);
		return subs;
	}
	void genSubsets(vector<int>& nums, int start, vector<vector<int>>& subs) {
		if (start >= nums.size()){
			subs.push_back(nums);
			return;
		}
		for (int i = start; i < nums.size(); i++) {
			swap(nums[start], nums[i]);
			//sub.push_back(nums[i]);
			genSubsets(nums, start + 1, subs);
			swap(nums[start], nums[i]);
			//sub.pop_back();
		}
	}
};

輸入：[1,1,2]

輸出：[[1,1,2],[1,2,1],[2,1,1]]

這個問題我的解決方法是在問題3的基礎上加上重複判斷，如果已經包含某個子集，直接略過。

當然還有更好的方法，待完成。

For example, given candidate set [2, 3, 6, 7] and target 7, 
A solution set is: 

[
  [7],
  [2, 2, 3]
]

同樣也是類似的遞迴方法

For example, given candidate set [10, 1, 2, 7, 6, 1, 5] and target 8, 
A solution set is: 

[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

和5稍有不同，遞迴時需要從下一個元素遍歷。

給出一個字串，找出其所有的迴文分割情況

For example, given s = "aab",
Return

[
  ["aa","b"],
  ["a","a","b"]
]

同樣也是類似的遞迴求解，不同的是需要判斷從start到i是否為迴文。

總結：

以上可歸為一類遞迴問題，思路相同，變化在於不同的要求，之所以後續沒有給出詳細解答，是因為希望學習能夠舉一反三，自己想明白和別人教明白是完全兩回事。

參考資料：