資料結構與演算法26-排序
排序
最簡單的排序實現
氣泡排序(Bubble Sort)一種交換排序,它的基本思想是:兩兩比較相鄰記錄的的關鍵字,如果反序則交換,直至沒有反序記錄為止。
如下:
/*對順序表L作交換排序(氣泡排序初級版)*/ void BubbleSort0(SqList *L) { int i,j; for(i=1;i<L->length;i++) { for(j=i+1;j<L->length;j++) { if(L->r[i]>L->r[j]) { swap(L,i,j); //交換 L->r[i]與L->r[j]的值 } } } }
這的思路就是讓每一個關鍵字,都和它後面的每一個關鍵字比較,如果大則交換,這樣第一位置的關鍵字在一次迴圈後,一定變成最小值。
它應該算是最最容易寫出的排序程式碼了,不過這個簡單易懂的程式碼,卻是有缺陷的。觀察後發現,在排序好1和2的位置後,對其餘關鍵字的排序沒有什麼幫助。也就是說,這個演算法的效率是非常低。
來看一個正宗的氣泡排序演算法
氣泡排序演算法
/*對順序表L作氣泡排序*/ void BubbleSort(SqList *L) { int i,j; for(i=1;i<L->length;i++) { for(j=L->length-1;j>=i;j--) { if(L->r[j]>L->r[j+1]){ swap(L,j,j+1); } } } }
當i=2時,變數j由8反向迴圈到2,逐個比較
氣泡排序優化
如我們要排序序列是{2,1,3,4,5,6,7,8,9}。也就是說,除了第一和第二的關鍵字需要交換外,別的都已經是正常順序。當i=1時,交換2和1,此時序列已經有序,但演算法仍然不依不饒地將i=2到9以及每個迴圈中的j迴圈都執行一遍,儘管並沒有交換資料,但是之後的大量比較還是大大地多餘了,
當i=2時,我們已經對9和8,8與7,….3與2作了比較,沒有任何資料交換,這就說明此序列已經有序,不需要再繼續後面的迴圈判斷了,為了實現這個想法,我們需要改進一下程式碼,增加一個標記變數flag來實現這一演算法的。
/*對順序表L作改進冒泡演算法*/
void BubbleSort2(SqList *L)
{
int i,j;
Status flag = TRUE;
for(i=1;i<L->length &&flag;i++)
{
flag=FALSE;
for(j=L->length-1;j>=i;j--)
{
if(L->r[j]>L->r[j+1]){
swap(L,j,j+1);
flag = TRUE;
}
}
}
}
簡單選擇排序
簡單選擇排序(Simple Selection Sort)就是通過n-i次關鍵字間的比較,從n-i+1個記錄中選出關鍵字最小的記錄,並和第i(1 i n)個記錄交換之。
/*對順序表L作簡單選擇排序*/
void SelectSort(SqList *L)
{
int i,j,min;
for(i=1;i<L->length;i++)
{
min = i;
for(j=i+1;j<L->length;j++)
{
if(L->r[min]>L->r[j])
min = j;
}
if(i!=min)
swap(L,i,min);
}
}
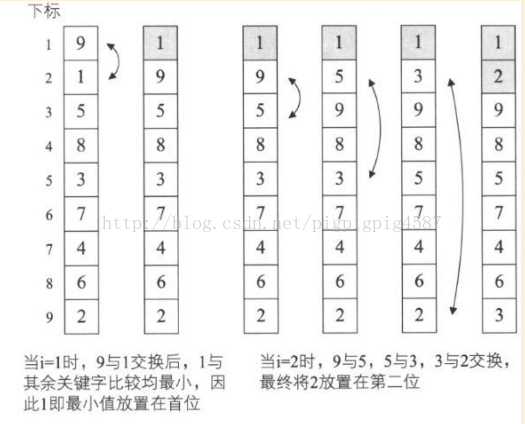
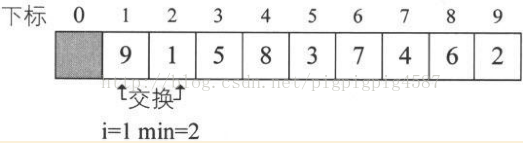
針對待排序的關鍵字序列是{9,1,5,8,3,7,4,6,2},對i從1迴圈到8。當i=1時,L.r[i]=9,min開始是1,然後與j=2到9比較L.r[min]與L.r[j]的大小,因為j=2時最小,所以min=2。最終交換了L.r[2]與L.r[1]的值。如圖,注意,這裡比較了8次卻只交換資料操作一次。
當i=2時,L.r[i]=9,min開始是2,經過比較後,min=9,交換L.r[min]與L.r[i]的值。這樣就找到了第二個位置
當i=3
之後資料比較和交換完全雷同,最多經過8次,就可以完成排序工作。
儘管於氣泡排序同為O(n2),但簡單選擇排序的效能上還是要略優於氣泡排序的
直接插入排序
直接插入排序(Straight Insertion Sort)的基本操作是將一個記錄插入到已經排好序的有序表中,從而得到一個新的、記錄數增1的有序表。
顧名思義,從名稱上也可以知道它是一種插入排序的方法。我們來看直接插入排序法的程式碼:
/*對順序表L作直接插入排序*/
void InsertSort(SqList *L)
{
int i,j;
for(i=2;i<L->length;i++)
{
if(L->r[i]<L->r[i-1])
{
L->r[0] = L->r[i];//設定哨兵
for(j=i-1;L->r[j]>L->L->r[0];j--)
L->r[j+1]=L->r[j];
L->r[j+1] = L->r[0]; //插入到正確位置
}
}
}
1. 程式開始執行,此時我們傳入的SqList引數的值為length=6,r[6]={0,5,3,4,6,2},其中r[0]=0將用於後面起到哨兵的作用。
2. 第4~13行就是排序的主迴圈。i從2開始的意思是我r[1]=5已經放好了位置,後面的資料其實就是插入到它的左側還是右側的問題。
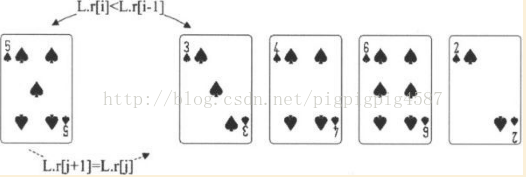
3. 第6行,此時i=2,L.r[i]=3比L.r[i-1]=5要小,因此執行第8~11行的操作。第8行,我們將L.r[0]賦值為L.r[i]=3的目的是為了起到9~10的迴圈終止判斷依據。下圖就是L.r[j+1]=L.r[j]的過程
4. 此時,第10行就是在移動完成後,突出了空位,然後第11行L.r[j+1]=L.r[0],將哨兵的值3賦值給j=0時的L.r[j+1],也就是說,將撲克牌3放置到L.r[1]的位置
5. 繼續迴圈,第6行,因為此時i=3,L.r[i]=4比L.r[i-1]=5要小,因此執行第8~11行程式碼操作,將5再右移一位,將4放置到當前5所在位置,
6. 再次迴圈,此時i=4。因為L.r[i]=6比L.r[i-1]=5要大,於是第8~11行程式碼不執行,此時前三張牌的位置沒變化,
7. 再次迴圈,此時i=5,因為L.r[i]=2比L.r[i-1]=6要小,因此執行第8~11行的操作。由於6、5、4、3都比2小,它們都將右移一位,將2放置到當前3所在位置。
希爾排序
所謂基本有序,就是小的關鍵字基本在前面,大的基本在後面,不大不小的基本在中間。
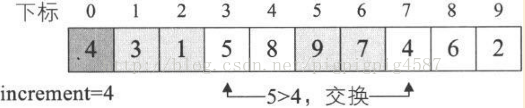
跳躍分割策略:將相距某個“增量”的記錄組成一個子序列,這樣才能保證在子序列內分別進行直接插入排序後得到結果是基本有序而不是區域性有序的
希爾排序程式碼如下:
void ShellSort(SqList *L)
{
int i,j;
int increment=L->length;
do
{
increment =increment/3+1; //增量序列
for(i=increment+1;i<L->length;i++)
{
if(L->r[i]<L->r[i-increment])
{//需將L->r[i]插入有序增量子表
L->r[0]=L->[i];
for(j=i-increment;j>0&&L->r[0]<L->r[j];j-=increment)
L->r[j+increment]=L->r[j];
L->r[j+increment]=L->r[0];
}
}
}
while(increment>1)
}
1. 程式開始執行,此時我們傳入的SqList引數的值為length=9,r[10]={0,9,1,5,8,3,7,4,6,2}。這就是我們需要等待排序的序列,
2. 第4行,變數increment就是那個“增量”,我們初始值讓它等於等待排序的記錄數。
3. 第5~19行是一個do迴圈,終止的條件是increment不大於1時,其實也就是增量為1時,就停止迴圈了。
4. 第7行,這一句很關鍵,但也是難以理解的地方,我們後面還要談到它,先放一放。這裡執行完後,increment = 9/3+1=4;
5. 第8~17行是一個for迴圈,i從4+1=5開始到9結束。
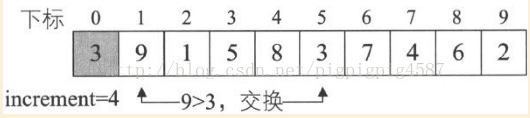
6. 第10行,判斷L.r[i]與L.r[i-increment]大小,L.r[5]=3小於L.r[i-increment]=L.r[1]=9,滿足條件,第12行,將L.r[5]=3暫存入L.r[0]。第13~14行的迴圈只是為了將L.r[1]=9的值賦給L.r[5],由於迴圈的增量是j-=increment,其實它就迴圈了一次,此時j=-3。第15行,再將L.r[0]=3賦值給L.r[j+increment]=L.r[-3+4]=L.r[1]=3。事實上,這一段程式碼就幹了一件事,就是將第5位的3和第1位的9交換了位置。
7. 迴圈繼續,i=6,L.r[6]=7> L.r[i-increment]=L.r[2]=1,因此不交換兩者資料。如圖
8. 迴圈繼續,i=7,L.r[7]=4<L.r[i-increment]=L.r[3]=5,交換兩者資料
9. 迴圈繼續,i=8,L.r[8]=6<L.r[i-increment]=L.r[4]=8,交換兩者資料。注意,第13~14行是迴圈,此時還要繼續比較L.r[5]與L.r[1]的大小,因為2<3,所以還要交換L.r[4]=8,交換兩者資料
10. 迴圈繼續,i=9,L.r[9]=2<L.r[i-increment]=L.r[5]=9,交換兩者資料。注意,第13~14行是迴圈,此時還要繼續比較L.r[5]與L.r[1]的大小,因為2<3,所以還要交換L.r[5]與L.r[1]的資料,如下圖
最終第一輪迴圈後,陣列的排序結果為下圖所示,細心的同學會發現,我們的數字1、2等小數字已經在前兩位,而8、9等大數已經在後兩位,也就是說,通過這樣的排序,我們已經讓整個序列基本有序了。這其實就是希爾排序的精華所在,它將關鍵字較小的記錄,不是一步一步地往前挪動,而是跳躍式地往前移,從而使得每次完成一輪迴圈後,整個序列就朝著有序堅實地邁進一步。
11. 我們繼續,在完成一輪do迴圈後,此時由於increment=4>1因此我們需要繼續do迴圈。第7行得到increment=4/3+1=2。第8~17行for迴圈,i從2+1=3開始到9結束。當i=3、4時,不用交換,當i=5時,需要交換資料,如圖
12. 此後,i=6,7,8,9均不交換,
13. 再次完成一輪do迴圈,increment=2>1,再次do迴圈,第7行得到increment=2/3+1,此時這就是最後一輪do迴圈了。儘管第8~17行,for迴圈,i從1+1=2開始到9結束,但由於當前序列已經基本有序,可交換資料的情況在為減少,效率其實很高。如圖,箭頭連線為需要交換的關鍵字如下:
最終排序如下
堆排序
如果可以做到每次在選擇到最小記錄的同時,並根據比較結果對其他記錄做出相應的調整,那樣排序的總體效率就會非常高了。而堆排序,就是對簡單選排序進行的一種改進。
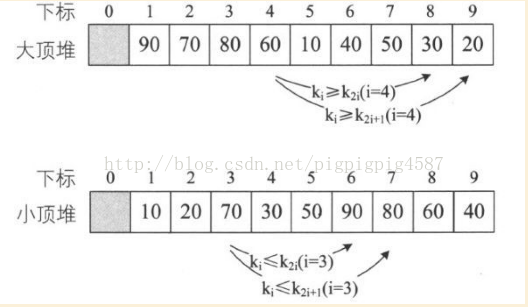
堆是具有下列性質的完全二叉樹:每個結點的值都大於或等於其左右孩子結點的值,稱為大頂堆;或者每個結點的值都小於或等於其左右孩子結點的值,稱為小頂堆。
這裡需要注意從堆的定義可知,根結點一定是堆中所有結點最大(小)者。較大(小)的結點靠近根結點(但也不絕對,比如右圖小頂堆,60、40均小於70,但它們並沒有70靠近根結點)。
如果按照層序遍歷的方式給結點從1開始編號,則結點之間滿足如下關係:
這裡為什麼i要小於等於
如果將上圖的大頂堆和小頂堆用層序遍歷存入陣列,則一定滿足上面的關係表示式如圖:
堆排序演算法
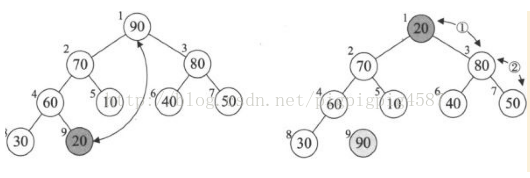
堆排序(Heap Sort)就是覽勝堆(假設利用大頂堆)進行排序的方法。它的基本思想是,將待排序的序列構造成一個大頂堆。此時,整個序列的最大值就是堆頂的根結點。將它移走(其實就是將其與堆陣列的未必元素交換,此時未尾元素就是最大值),然後將剩餘的n-1個序列重新構造一個堆,這樣就會得到n個元素中次大值,如此反覆執行,便能得到一個有序序列了。
例如圖所示,圖①是一個大頂堆,90為最大值,將90與20(末尾元素)互換,如圖②所示,此時90就成了整個堆序列的最後一個元素,將20經過調整,使得90以外的結點繼續滿足大頂堆定義(所有結點都大於等於其子孩子)見圖③,然後再考慮將30與80互換….
相信大家有些明白堆排序的基本思想了,不過要實現它還需要解決兩個問題:
1. 如何由一個無序序列構建成一個堆?
2. 如果在輸出堆頂元素後,調整剩餘元素成為一個新的堆?
/*對順序表L進行堆排序*/
void HeapSort(SqList *L)
{
int i;
for(i=L->length/2;i>0;i--)
HeapAdjust(L,i,L->length);
for(i=L->length;i>1;i--)
{
swap(L,1,i); //將堆頂記錄和當前未經排序子序列的最後一個記錄交換
HeapAdjust(L,1,i-1);//將L->r[i…i-1]重新調整為大頂堆
}
}
從程式碼也可以看出,整個排序過程分為兩個for迴圈。第一個迴圈要完成的就是將現在的待排序序列構建成一個大頂堆。第二個迴圈要完成的就是逐步將每個最大值的根結點與末尾元素交換,並且再調整其成為大頂堆。
假設我們要排序的序列是{50,10,90,30,70,40,80,60,20},那麼L.length=9,第一個for迴圈,程式碼第4行,i是從[9/2]=4開始,4->3->2->1的變數變化。為什麼不是從1到9或者從9到1,而是從4到1呢?其實我們看了下圖就明白了,它們都有什麼規律?它們都是有孩子的結點。注意灰色結點的下標編號就是1,2,3,4。
我們所謂的將待排序的序列構建成為一個大頂堆,其實就是從下往上、從右到左,將每個非終端結點(非葉結點)當作根結點,將其和其子樹調整成大頂堆。i的4->3->2->1的變數,其實也就是30,90,10,50的結點調整過程。既然已經弄清楚i的變化是在調整如些元素了,現在我們來看關鍵的HeapAdjust(堆調整)函式是如何實現的。
/*已知L->r[s..m]中記錄的關鍵字除L->r[s]之外均滿足堆的定義*/
/*本函式調整L->r[s]的關鍵字,使L->[s..m]成為一個大頂堆*/
void HeadAdjust(SqList *L,int s,int m)
{
int temp,j;
temp=L->r[s];
for(j=2*s;j<=m;j*=2)/*沿關鍵字較大的孩子結點向下篩選*/
{
if(j<m&&L->r[j]<L->r[j+1])
++j; /*j為關鍵字中較大的記錄的下標*/
if(temp>=L->r[j])
break; /*rc應插入在位置s上*/
L->r[s]=L->r[j];
s=j;
}
L->r[s]=temp; //插入
}
1. 函式第一次呼叫時,s=4,m=9,傳入的Sqlist引數的值為length=9,r[10]={0,50,10,90,30,70,40,80,60,20}。
2. 第4行,將L.r[s]=L.r[4]=30,賦值給temp,如圖
3. 第5~13行,迴圈遍歷其結點的孩子。這裡j變數為什麼是從2*s開始呢?又為什麼是j*=2遞增呢?原因還是二叉樹的性質5,因為我們這棵是完全二叉樹,當前結點序號是s,其左孩子的序號一定是2s,右孩子的序號一定是2s+1,它們的孩子當然也是以2的位數序號增加,因此j變數才這樣迴圈。
4. 第7~8行,此時j=2*4=8,j<m說明它不是最後一個結點,如果L.r[j]<L.r[j+1],則說明左孩子小於右孩子。我們的目的是要找到較大值,當然需要讓j+1以便變成指向右孩子的下標。當前30的左右孩子是60和20,並不滿足此條件,因此j還是8。
5. 第9~10行,temp=30,L.r[j]=60,並不滿足條件。
6. 第11~12行,將60賦值給L.r[4],並令s=j=8。也就是說,當前算出,以30為根結點的子二叉樹,當前最大值是60,在第8的位置。注意此時L.r[4]和L.r[8]的值均為60
7. 再迴圈因為j=2*j=16,m=9,j>m,因此跳出迴圈。
8. 第14行,將temp=30賦值給L.r[s]=L.r[8],完成30與60的交換工作。本次函式呼叫完成。
9. 再次呼叫HeapAdjust,此時s=3,m=9。第4行,temp=L.r[3]=90,第7~8行,由於40<80得到j+1=2*s+1=7。9~10行,由於90>80,因此退出迴圈,最終本次呼叫,整個序列未發生什麼改變。
10. 兩次呼叫HeapAdjust,此時s=2,m=9。第4行,temp=L.r[2]=10,第7~8行,60<70,使得j=5。最終本次呼叫使得10與70進行了互換,如下圖
11. 再次呼叫HeapAdjust,此時s=1,m=9。第4行,temp=L.r[1]=50,第7~8行,70<90,使得j=3。第11~12行,L.r[1]被賦值了90,並且s=3,再迴圈,由於2j=6並未大於m,因此再次執行迴圈體,使得L.r[3]被賦值了80,完成迴圈後,L.r[7]被賦值為50,最終本次呼叫使得50、90、80進行了輪換,如圖
到此為止,我們構建大頂堆的過程算是完成了,也就是HeapSort函式的第4~5行迴圈執行完畢。
接下來HeapSort函式的第6~11行就是正式的排序過程,由於有了前面充分準備,其實這個排序就比較輕鬆了。如下
for(i=L->length;i>1;i--)
{
swap(L,1,i); //將堆頂記錄和當前未排序子序列的最後一個記錄交換
HeapAdjust(L,1,i-1); //將L->r[1..i-1]重新調整為大頂堆
}
1. 當i=9時,第8行,交換20與90,第9行,將當前的根結點20進行大頂堆調整,調整過程和剛才流程一樣,找到它左右子結點的較大值,互換,再找到其子結點的較大值互換。此時序列變為{80,70,50,60,10,40,20,30,90}
2. 當i=8時,交換30與80,並將30與70交換,再與60交換,此時序列變為{70,60,50,30,10,40,20,80,90}
如圖
3. 後面的變化完全類似,不解釋瞭如圖
歸併排序
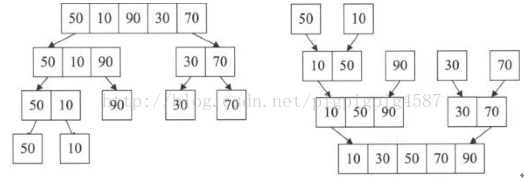
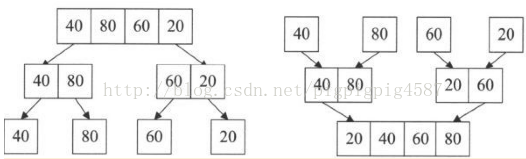
如圖我們將本是無序的陣列序列{16,713,10,9,15,3,2,5,8,12,1,11,4,6,14},通過兩兩合併排序後再合併,最終獲得一個有序的陣列。注意仔細觀察它的形狀,你會發現,它像極了一棵倒置的完全二叉樹,通常涉及到完全二叉樹結構的排序演算法,效率一般都不低的。
兼併排序:就是利用歸併的思想實現的排序方法。它的原理是假設初始序列含有n個記錄,則可以看成是n個有序的子序列,每個子序列的長度為1,然後兩兩歸併,得到[n/2]([x]表示不小於x的最小整數)個長度為2或1的有序子序列;再兩兩歸併,….,如此重複,直至得到一個長度為n的有序序列為止,這種排序方法稱為2路歸併排序
程式碼如下:
void MergeSort(SqList *L)
{
MSort(L->r,L->r,1,L->length);
}
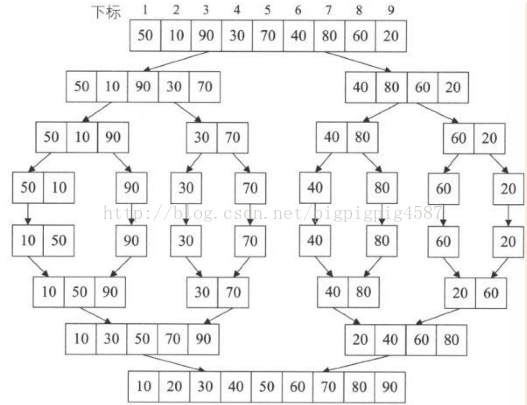
由於我們要講解的歸併排實現需要用到遞迴呼叫,因此我們外封裝一個函式。假設現在要對陣列{50,10,90,30,70,40,80,60,20}進行排序,L.length=9,我們來看一下MSort的實現
/*將SR[s..t]歸併排序為TR1[s..t]*/
void MSort(int SR[],int TR1[],int s,int t)
{
int m;
int TR2[MAXSIZE+1];
if(s==t)
TR1[s]=SR[s];
else
{
m=(s+t)/2;
MSort(SR,TR2,s,m);
MSort(SR,TR2,m+1,t);
Merge(TR2,TR1,s,m,t)
}
}1. MSort被呼叫時,SR與TR1都是{50,10,90,30,70,40,80,60,20},s=1,t=9,最終我們的目的就是要將TR1中的陣列排好序。
2. 第5行,顯然s不等於t,執行第8~13行語句塊。
3. 第9行,m=(1+9)/2=5。m就是序列的正中間下標。
4. 此時第10行,呼叫MSort(ST,TR2,1,5);的目標就是將陣列SR中的第1~5的關鍵字歸併到有序TR2(呼叫前TR2為空陣列),第11行,呼叫MSort(SR,TR2,6,9)呼叫的目標就是將陣列SR中的第6~9的關鍵字歸併到有序TR2。也就說,在呼叫這兩句程式碼之前,程式碼已經準備將陣列分成兩組了
5. 第12行,函式Merge程式碼細節一會再講,呼叫Merge(TR2,TR1,1,5,9)目標其實就是將第10和11行程式碼獲得的陣列TR2(注意它是下標為1~5和6~9的關鍵字分別有序)歸併為TR1,此時相當於整個排序就已經完成了
6. 再來看第10行遞迴呼叫進去後,s=1,t=5,m=(1+5)/2=3。此時相當於將5個記錄拆分為三個和兩個。繼續遞迴進去,直到細分為一個記錄填入TR2,此時s與t相等,遞迴返回,每次遞迴返回後都會執行當前遞迴函式的第12行,將TR2歸併到TR1中,最終使得當前序列有序。
7. 同樣的第11行也是類似方式
8. 此時也就是剛才所講的最後一次執行第12行程式碼,將{10,30,50,70,90}與{20,40,60,80}歸併為最終有序的序列
/*將有序的SR[i..m]和SR[m+1..n]歸併為有序的TR[i…n]*/
void Merge(int SR[],int TR[],int i,int m,int n)
{
int j,k,l;
for(j=m+1,k=i;i<=m&&j<=n;k++)
{
if(SR[i]<SR[j])
TR[k]=SR[i++];
else
TR[k] = SR[j++];
}
if(i<=m)
{
for(l=0;l<=m-i;l++)
TR[k+1]=SR[i+1];
}
if(j<=n)
{
for(l=0;l<=n-j;l++)
TR[k+1]=SR[j+1];
}
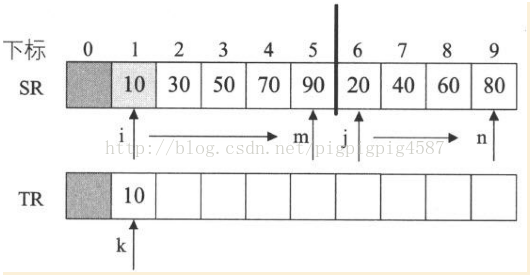
}1. 假設我們此時呼叫的Merge就是將{10,30,50,70,90}與{20,40,60,80}歸併為最終有序的序列,因此陣列SR為{10,30,50,70,90,20,40,60,80},i=1,m=5,n=9。
2. 第4行,for迴圈,j由m+1=6開始到9,i由1開始到5,k由1開始每次加1,k值用於目標陣列TR的下標。
3. 第6行,SR[i]=SR[1]=10,SR[j]=SR[6]=20,SR[i]<SR[j],執行第7行,TR[k]=TR[1]=10,並且i++
4. 再次迴圈,k++得到k=2,SR[i]=SR[2]=30,SR[j]=SR[6]=20,並且j++,如圖
5. 再次迴圈,k++得到k=3,SR[i]=SR[2]=30,SR[j]=SR[7]=40,SR[i]<SR[j],執行第7行,TR[k]=TR[3]=30,並且i++,如圖
6. 接下來完全相同的操作,一直到j++後,j=10,大於9退出迴圈,如圖
7. 第11~20行程式碼,其實就將歸併剩下的陣列資料,移動到TR的後面。當前k=9,i=m=5,執行第13~20行程式碼,for迴圈l=0,TR[k+1]=90,大功造成。
就這樣,我們歸併排序就算是完成了一次排序工作,怎麼樣,和堆排序比,是不是要簡單一些呢?
非遞迴實現歸併排序
歸併排序大量引用遞迴,儘管在程式碼上比較清晰,容易理解,但這會造成時間和空間上的效能損耗。我們排序追求的就是效率,有沒有可能將遞迴轉化為迭代呢?結論當然是可以的,而且改動之後效能上進一步提高,程式碼如下:
void MergeSort2(SqList *L)
{
int* TR=(int *)malloc(L->length*sizeof(int));
int k=1;
while(k<L->length)
{
MeragePass(L->r,TR,k,L->length);
k=2*k;
MergePass(TR,L->r,k,L->length);
k=2*k;
}
}1. 程式開始執行,陣列L為{50,10,90,30,70,40,80,60,20},L.length=9。
2. 第3行,我們事先申請額外的陣列記憶體空間,用來存放歸併結果。
3. 第5~11行,是一個while迴圈,目的是不斷地歸併有序序列。注意k值變化,第8行與第10行,在不斷迴圈中,它將由1->2->4->8->16,跳出迴圈。
4. 第7行,此時k=1,MergePass函式將原來的無序陣列兩兩歸併入TR
5. 第8行,k=2。
6. 第9行,MergePass函式將TR中已經兩兩歸併的有序序列再次歸併回陣列L.r中如下圖
7. 第10行,k=4,因為k<9,所以繼續迴圈,再次歸併,最終執行完第7~10行,k=16,結束迴圈,完成排序工作
從程式碼中,我們能夠感受到,非遞迴的迭代做法更加直截了當,從最小的序列開始歸併直至完成。不需要像歸併的遞迴演算法一樣,需要先拆分遞迴,再歸併退出遞迴。程式碼如下:
void MergePass(int SR[],int TR[],int s,int n)
{
int i=1;
int j=;
while(i<n-2*s+1)
{
Merge(SR,TR,i,i+s-1,i+2*s-1);
i=i+2*s;
}
if(i<n-s+1)
Merge(SR,TR,i,i+s-1,n);
else
for(j=i;j<=n;j++)
TR[j] = SR[j];
}
1. 程式執行。我們第一次呼叫MergePass(L.r,TR,L.length);此時L.r是初始無序狀態,TR為新申請的空陣列,k=1,L.length=9。
2. 第5~9行,迴圈的目的就兩兩歸併,因s=1,n-2*s+1=8,為什麼迴圈i從1到8,而不是9呢?就是因為兩兩歸併,最終第9條記錄定剩下來,無法歸併
3. 第7行,Merge函式我們前面已經詳細講過,此時i=1,i+s-1,i+2*s=2。也就是說,我們將SR(即L.r)中第一個和第二個記錄歸併到TR中,然後第8行i=i+2*s=3,再迴圈,我們就是將第三個和第四個記錄歸併到TR中,一直到第七和第八個記錄歸併,
4. 第10~14行,主要是處理最後的尾數,第11行是說將最後剩下的多個記錄歸併到TR中。不過由於i=9,n-s+1=9,因此執行第13~14行。將20放入到TR陣列的最後,如圖
5. 再次呼叫MergePass時,s=2,第5~9行的迴圈,由第8行的i=i+2*s可知,此時i就是以4為增量進行迴圈了,也就是說,是將兩個有兩個記錄的有序序列進行歸併為四個記錄的序列。最終再將最後剩下的第9條記錄"20"插入TR。如圖
6. 後面類似(多推幾次就熟啦)。
使用歸併排序時,儘量考慮用非遞迴方法。
快速排序
我們現在要學習的快速排序演算法,被列為20世紀十大演算法之一。
希爾排序相當於直接排序的升級,它們屬於插入排序類,堆排序相當於簡單選擇排序的升級,它們同屬於選擇排序類,而快速排序其產是我們前面認為最慢的氣泡排序的升級,它們都屬於交換排序類。即它也是通過不斷比較和移動交換來實現排序的,只不過它的實現,增大了記錄的比較和移動的距離,將關鍵字較大的記錄從前面直接移動後面,關鍵字較小的記錄從後面直接移動前面,從而減少總的比較次數和移動交換次數。
演算法的基本思想是:通過一趟排序將待排記錄分割成獨立的兩部分,其中一部分記錄的關鍵字比另一部分記錄的關鍵字小,則分別對這兩部分記錄繼續進行排序,以達到整個序列有序的目的。
假設要對陣列{50,10,90,30,70,40,80,60,20}進行排序。我們通過程式碼的講解來學習快速排序。我們來看程式碼:
void QuickSort(SqList *L)
{
QSort(L,1,L->length);
}
又是一句程式碼,和歸併排序一樣,由於需要遞迴呼叫,因此我們外封裝一個函式。現在我們來年Qosrt的實現
/*對順序表L中的子序列L->r[low ...high]作快速排序*/
void QSort(SqList *L,int low ,int high)
{
int pivot;
if(low<high)
{
pivot =Partition(L,low,high);
QSort(L,low,pivot-1);
QSort(L,pivot+1,high);
}
}
我呼叫這個函式時我們理解QSort(L,1,L->length)中的1和L->length它就是當前待排序的序列最小下標low和最大下標high。
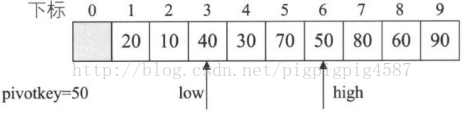
Partition函式要做的,就是選取當中一個關鍵字,比如選擇第一個關鍵字50,然後想盡辦法將它放到一個位置,使得它左邊的值都比它小,右邊的值都比它大,我們將這樣的關鍵字稱為樞軸(pivot)。
在經過Paitition(L,1,9)的執行之後,陣列變成{20,10,40,30,50,70,80,60,90},並返回值5給pivot,數字5表明50放置在陣列下標為5的位置。此時,計算機把原來的陣列變成了兩個位於50左和右的小陣列{20,10,40,30,} {70,80,60,90},而後的遞迴呼叫QSort(L,1,5-1);QSort(L,5+1,9);語句其實就是對這兩個陣列分別進行Partition操作,直到順序全部正確為止。
我們來看看快速排序的關鍵函式Partition函式
/*交換順序表L中的子表記錄,使樞軸記錄到位,並返回其位置*/
/*此時在它之前的記錄均不大於它*/
int Partition(SqList *L,int low,int high)
{
int pivotkey;
pivotkey=L->r[row];
while(low<high)
{
while(low<high&&L->r[high]>=pivotkey)
high--;
swap(L,low,high);
while(low<high&&L->r[low]<=pivotkey)
low++;
swap(L,low,high);
}
return low;
}
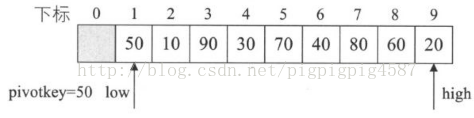
1. 程式開始執行,此時low=1,high=L.length=9。第4行,我們將L.r[low]=L.r[0]=50賦值給樞軸變數pivotkey,
2. 第5~13行為while迴圈,目前low=1<high=9執行內部語句
3. 第7行,L.r[high]=L.r[9]=20不大於pivotkey=50,因此不執行第8行
4. 第9行交換資料L.r[1]=20,L.r[9]=50。為什麼要交換,就是因為通過第7行的比較知道,L.r[high]是比pivotkey=50還要小的值,因此它應該交換到50左側。
5. 第10行,當L.r[low]=L.r[1]=20,pivotkey=50,L.r[row]<pivotkey,因此第11行,low++,此時low=2。繼續迴圈,L.r[2]=10<50,low++,此時low=3,L.r[3]=90>50,退出迴圈。
6. 第12行,交換L.r[low]=L.r[3]與L.r[high]=L.r[9]的值,使得L.r[3]=50,L.r[9]=90。此時相當於將一個比50大的值90交換到50的右邊,注意此時low已經指向3,
7. 繼續第5行,因為low-3<high=9執行迴圈體。
8. 第7行,當L.r[high]=L.r[9]=90,pivotkey=50,L.r[high]>pivotkey,因此第8行,high--,此時high=8,繼續迴圈,L.r[8]=60>50,high--,此時high=7。L.r[7]=80>50,high--,此時high=6。L.r[6]=40<50,退出迴圈。
9. 第9行交換L.r[low]=L.r[3]=50與L.r[high]=L.r[6]=40的值,使得L.r[3]=40,L.r[6]=50。
10. 第10行,當L.r[low]=L.r[3]=40,pivotkey=50,L.r[low]<pivotkey,因此第11行,low++,此時low=4。繼續迴圈L.r[4]=30<50,low++,此時low=5。L.r[5]=70>50退出迴圈。
11. 第12行交換L.r[row]=L.r[5]=70與L.r[high]=L.r[6]=50的值,使得L.r[5]=50,L.r[6]=70。如圖
12. 再次迴圈。因為low=5<high=6,執行迴圈體後,low=high=5,退出迴圈如圖
13. 最後第14行,返回low的值5,函式執行完成,接下來就是遞迴呼叫QSort(L,1,5-1);和QSort(L,5+1,9)。其實就是對{20,10,40,30}和{70,80,60,90}分別進行同樣的Partition操作,直到順序全部正確為止。
快速排序的優化
優化選取樞軸
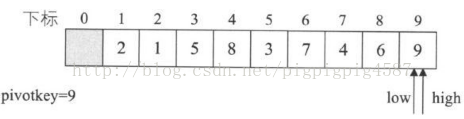
如果我們排序陣列是{9,1,5,8,3,7,4,6,2}由程式碼第4行pivotkey=L->r[row] 我們應該選取9作為第一個樞軸pivotkey。此時,經過一輪pivot=Partition(L,1,9)轉換後,它只是更換了9的與2的位置,並且返回9給pivot,整個系列並沒有實質性的變化如圖
固定選擇第一個關鍵字
隨機選擇樞軸法
三數取中法。即取三個關鍵字先進行排序,將中間的數作為樞軸,一般是取左端、右端和中間三個數,也可以隨機取。
我們來看看取左端、右端和中間三個數的實現程式碼,在Partition函式程式碼的第3行與第4行之間增加這樣一段程式碼。
int m=low+(high-low)/2; //中間下標
if(L->r[low]>L->r[high])
swap(L,low,high); //保證左邊的小右邊的大
if(L->r[m]>L->r[high])
swap(L,high ,m); //保證中間的比右邊的小
if(L->r[m]>L->r[low])
swap(L,m,low); //保證左邊比中間的小