關於梯度上升法和梯度下降法的原理，大多數都是純理論的解釋和公式的推導，沒有一種直觀的表達方式。

在這我分別舉出兩個簡單而又直觀的例子，大家就明白了，為什麼梯度下降法一定是減梯度，而梯度上升法一定是加梯度。

對於梯度下降法來說，在神經網路中用到，最小化誤差的一種優化方法。

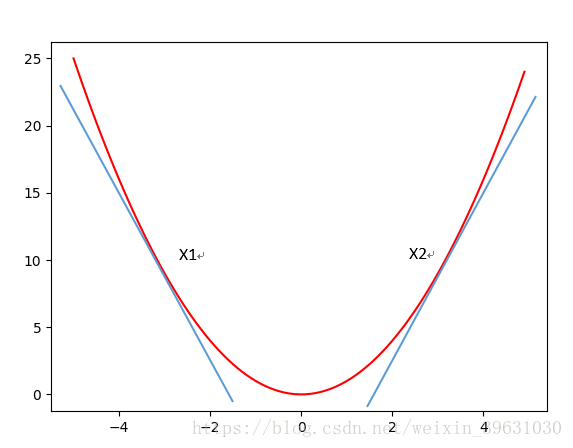
如用梯度下降法求此函式的極小值，

在x1,x2點分別可導，

在x1處導數為負數，在此函式中，(-∞,0)區間，對任意一點xi，導數都為負數；

在x2處導數為正數，在此函式中，(0,+∞)區間，對任意一點xi，導數都為正數；

這樣，在梯度下降中，公式 就容易解釋了，在(-∞,0)區間，導數為負數，更新的在增大（比如原來的xi處於點x=-4，在向最小值y逼近的時候，x一直在增大），一直向最低點逼近；同樣在(0,+∞)區間，導數

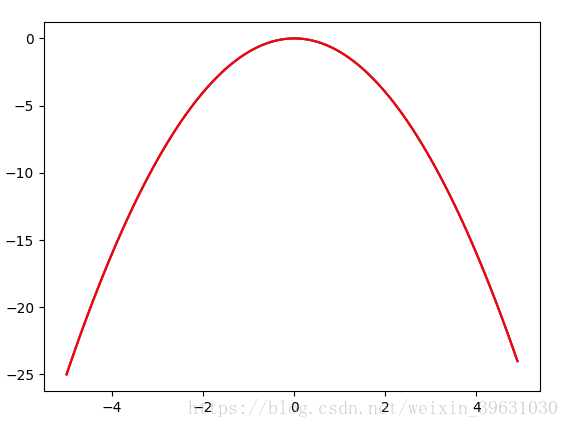
在梯度上升法是在邏輯迴歸中求概率最大值，即求最大似然函式的最大值用到的方法，

求的極大值為例；

在此函式中，(-∞,0)區間，對任意一點xi，導數都為正數；

                      (0,+∞)區間，對任意一點xi，導數都為負數；

在梯度上升中，公式 在(-∞,0)區間，導數為正數，更新的在增大，一直逼向最高點；同樣在(0,+∞)區間，導數為負數，在減小，一直向最高點逼近。

反向推理，就能明白梯度上升為什麼是加梯度，而梯度下降是減梯度。