題意：給n!個n的排列，按字典序從小到大連成一條序列，例如3的情況為：[1,2,3, 1,3,2, 2,1,3 ,2,3,1 ,3,1,2 ,3,2,1],問其中長度為n，且和為sum=n*(n+1)/2的序列有多少個？
（題意來自於：https://www.cnblogs.com/pkgunboat/archive/2018/12/31/10201676.html @維和戰艇機，感謝你這麼好的總結方式，借用一下希望不要介意）

思路（非官方題解）：官方題解下面有種方法是：There is also a simple recurrence counting the same answer, found by arsijo:d(n)=(d(n−1)+(n−1)!−1)⋅n，我比賽時是用這個方法。

如官方題解思路，有兩種n長度的子序列符合和為n*(n-1)/2：
第一種為n！個組成序列的排列；
第二種為一部分在一個排列中，另一部分在下一個排列中的排列。
顯而易見，第一種有n！種情況，那下面來推第二種：

對於一個n長度的排列，假設我們先固定前k個元素，那麼對於包含這些前k個元素固定的片段，是一系列①前k個元素固定；②後n-k個元素按照字典序從小到大的排列連線而成的，假設這一系列排列的數量為m。

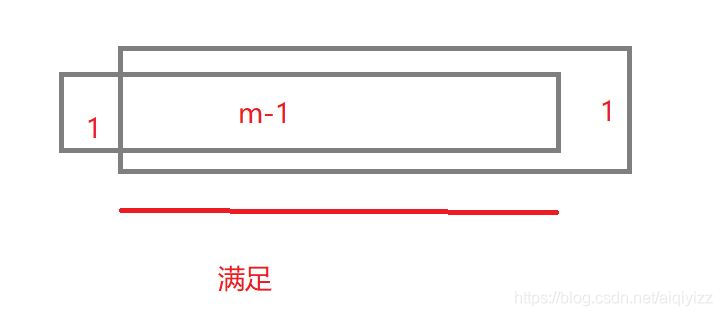
發現這個有什麼用呢？現在取出上面那段片段，我們來尋找裡面排列為③使用一個排列後n-k個元素④使用下一個排列前k個元素的排列的數量，在上面片段中，能找到的排列都滿足，而又由於這些排列夾在上面排列兩兩之間，可得數量為m-1。（就像對於一個隊伍的小朋友，假設兩兩之間插入一個小朋友，那麼插入小朋友的數量為原隊伍小朋友的數量-1）。
那麼有沒有漏網之魚呢？答案是沒有。這個草稿紙上畫下，你就明白了。m中滿足條件的有m-1種，說明只有一種是不滿足的。對於假設考慮只滿足③的，那麼片段的第一個排列是不滿足的，考慮只滿足④的話，片段的最後一個排列是不滿足的。就不展開了。（不會暴露樓主不想打，，，咔咔）

知道上述公式後，來求答案：
k∈[1,n]；
當k=n時，其實就是組成序列的排列，所以用組成序列排列的公式：n！；
當k!=n時，用上面得出的公式A(n,n-k)*(k!-1)；
因此答案是n!+∑(k from 1 to n-1) [A(n,n-k)×(k!-1)]。

#include<stdio.h>
typedef long long ll;
const int maxn = 1e6 + 5;
const ll Mod = 998244353;
	ll a,jie[maxn],djie[maxn],n,res; //jie,djie分別是階乘和A(n,n-k)，res是結果
	
int main()
{
	scanf("%I64d",&n);
	jie[0] = 1; djie[0] = 1;
	for(a = 1;a <= n;a ++)
	{
		jie[a] = jie[a-1] * a % Mod;
		djie[a] = djie[a-1] * (n+1-a) % Mod;		
	}
	res = jie[n];
	for(a = 2;a <= n-1;a ++)
		res = (res + (jie[a] - 1) * djie[n-a] % Mod) % Mod;
	printf("%I64d\n",res);
	return 0;
}