AC自動機詳解(無指標)
1. 什麼是AC自動機?
define
Aho-Corasick automation,該演算法在1975年產生於貝爾實驗室,是著名的多模匹配演算法。——百度百科
具體來說,就是像搜尋引擎一樣,在搜尋欄裡輸入幾個keyword,然後在大量的網頁文本里尋找這些關鍵字出現的次數
前決知識——KMP,trie
這不得不令人想起AC自動機的小弟,KMP演算法
KMP實質上是單模匹配,一個keyword對整個文字的搜尋
也正因為KMP與AC自動機關係像大哥與小弟一樣,掌握AC自動機必須先掌握KMP
2. 如何實現?
在上文中已經說過了,要掌握AC自動機,首先掌握KMP和trie樹(字典樹)
在這裡不展開講解,簡單提幾句即可
(1)KMP,trie
KMP
目的:單關鍵詞查詢
本質:超級優化後的暴力
實現:維護出模式串的最長公共前後綴陣列nxt,在主串和模式串一一匹配的過程中利用nxt陣列實現排除重複掃描的跳躍式查詢,從而提高了搜尋效率
trie樹
目的:用樹結構來儲存字串
本質:多叉樹
實現:
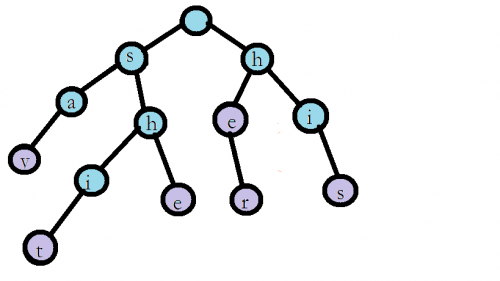
(從 https://blog.csdn.net/Whispers_zmf/article/details/80809609 大佬那裡摳的圖 )
這就是一棵trie樹,儲存了say,shit,she,he,her,his幾個單詞
不要在意細節
我們定義一個空的根節點,給它26個空的子節點分別代表a~z(具體情況具體分析),然後我們將要插入的每一個字串的首字母以ascll碼代表邊的標號的方式將這個字母壓在邊上,對於每個子節點也進行同樣的操作
具體實現程式碼如下
#define calcid(a) a-97
int tree[maxn][26];
int flag[maxn];
inline void insert(char *s)//插入字串s
{
int len=strlen(s);
int root=0;
for(int i=0;i<len;i++)
{
int id=calcid(s[i]);//每一條邊的編號
if(tree[root][id]==0)//0代表節點root的id號邊的節點還為空,於是為其分匹配記憶體
{
tree[root][id]=++cnt;//cnt代表著節點的編號,有點像鏈式前向星 (2)AC自動機
鳥瞰
思想:在trie樹裡跑KMP
核心:fail指標的構建
流程:
1.建trie樹
2.在trie樹裡構建fail指標
3.將trie樹與主串匹配求解
細節
1.trie樹
常規的AC自動機裡的trie樹與一般的trie相比沒有什麼太大的區別,只是要注意樹上節點個數的估計和附加資訊的維護(比如flag)
2.fail指標的構建
這是AC自動機的精華
目的:fail在KMP裡叫做nxt(懂了吧~~)
具體定義:節點u的fail指向v,v是以u代表的字元為結尾的最長當前字串的最長合法真字尾的最後一個節點(可真繞)

就像上圖
找靠左的節點i的fail指標,
由於以i結尾的當前字串(以第二層的節點開頭,結尾不限)的字尾有shi,hi,i
而shi不是真字尾,hi,i不合法(不合法指沒有與當前字尾完全相同的當前字串),且hi的長度最長,因此滿足要求的最長當前字串的最長合法真字尾是hi,於是找到i的fail指標如下
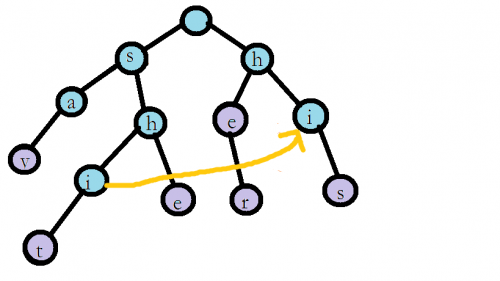
當然,如果某節點的所有真字尾都非法,那麼就將其指向0號節點即可
於是有下圖
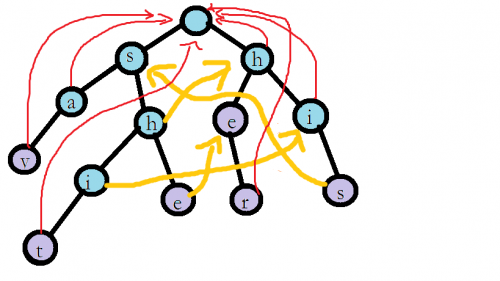
(第二層的s節點和第三層的e節點連向根節點 太懶不想改)
構建:
仔細觀察上圖,我們可以發現一些有意思的規律
1.第二層的fail指標的規律
2.沿著fail指標走,深度會越來越小
3.若將fail指標和邊都一視同仁的看作有向邊的話,整個trie樹就成了一個強聯通分量,可以相互到達
4.如果a節點的fail指向了b節點,那麼a節點的t兒子的fail指向b節點的t兒子(如果兒子不存在,就指根)
這些規律中,第4條對我們構建fail指標有很大幫助
據第四條,我們不難發現,只要確定了第s層的所有點的fail指標,就可以以此來確定第s+1層的所有的點的fail指標
自然而然就想到用一個bfs來維護fail指標
code:
void buildfail()
{
queue<int>q;
for(int i=0;i<26;i++)
{
if(tree[0][i])
{
fail[tree[0][i]]=0;
q.push(tree[0][i]);
}
}//更新第二層的fail並開始bfs
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=0;i<26;i++)//列舉u的每一條出邊
{
if(tree[u][i])//如果存在
{
fail[tree[u][i]]=tree[fail[u]][i];//用規律4更新其fail
q.push(tree[u][i]);
}
else tree[u][i]=tree[fail[u]][i];// 如果不存在這個點,我們就將這個空點連向u的fail點的i兒子
}
}
3.匹配求解
在構建了trie樹和fail指標後,是時候來求解了
如何求解?
對於未知的主串s來說,它的任何一個字母都有可能是一個模式串,因此在求解時很明顯應該一個字元一個字元來求解
於是首先來一個迴圈,對每一個主串字元,用fail指標對這個字元的所有字首進行一次遍歷查詢,統計出這個字元的答案然後累加即可
#define calcid(a) a-97
int count(char *s)
{
int len=strlen(s);
int now=0;//now初始是根節點
int ans=0;//累加
for(int i=0;i<len;i++)//對每一個字元s[i]求解
{
int id=calcid(s[i]);
now=tree[now][id];
for(int t=now;t&&~flag[t];t=fail[t])
{
ans+=flag[t];
flag[t]=-1;
}
}
return ans;
}
可能以下這段程式碼不是很好理解,因為這是fail指標的精華所在
for(int t=now;t&&~flag[t];t=fail[t])
{
ans+=flag[t];
flag[t]=-1;
}
由於fail指標是指向與該節點表示串字尾相等的且長度最大的串(或字首)的節點
故這個迴圈其實是為了統計當前列舉到的字元是多少個當前字串的字尾
換句話說這個過程就是在遍歷當前構成的字串的字尾中是否有其他的單詞
以上就是AC自動機的基礎內容,下面附上本人奇醜無比的程式碼
luogu模版題
#include<bits/stdc++.h>
using namespace std;
//**********************************data
#define calcid(a) a-97
const int maxn=1e6+10;
int n,cnt;
int tree[maxn][26];
int flag[maxn];
int fail[maxn];
//**********************************function
inline void insert(char *s)//插入字串s
{
int len=strlen(s);
int root=0;
for(int i=0;i<len;i++)
{
int id=calcid(s[i]);//每一條邊的編號
if(tree[root][id]==0)//0代表節點root的id號邊的節點還為空,於是為其分匹配記憶體
{
tree[root][id]=++cnt;//cnt代表著節點的編號,有點像鏈式前向星
flag[cnt]=0;//flag[u]表示以u號節點所連的邊代表的字元結尾的單詞個數
for(int i=0;i<26;i++)tree[tree[root][id]][i]=0;//初始化
}
root=tree[root][id];//將root指向下一層
}
flag[root]++;
}
void buildfail()
{
queue<int>q;
for(int i=0;i<26;i++)
{
if(tree[0][i])
{
fail[tree[0][i]]=0;
q.push(tree[0][i]);
}
}//更新第二層的fail並開始bfs
while(!q.empty())
{
int u=q.front();q.pop();
for(int i=0;i<26;i++)//列舉u的每一條出邊
{
if(tree[u][i])//如果存在
{
fail[tree[u][i]]=tree[fail[u]][i];//用規律4更新其fail
q.push(tree[u][i]);
}
else tree[u][i]=tree[fail[u]][i];
// 如果不存在這個點,我們就將這個空點連向u的fail點的i兒子
}
}
}
int count(char *s)
{
int len=strlen(s);
int now=0;//now初始是根節點
int ans=0;//累加
for(int i=0;i<len;i++)//對每一個字元s[i]求解
{
int id=calcid(s[i]);
now=tree[now][id];
for(int t=now;t&&~flag[t];t=fail[t])
{
ans+=flag[t];
flag[t]=-1;
}
}
return ans;
}
//**********************************main
int main()
{
//freopen("datain.txt","r",stdin);
//freopen("dataout.txt","w",stdout);
char s[maxn];
//memset(tree,-1,sizeof(tree));
//memset(flag,0,sizeof(flag));
cnt=0;
scanf("%d",&n);
memset(tree[0],0,sizeof(tree[0]));
for(int i=0;i<n;i++)
{
scanf("%s",s);
insert(s);
}
buildfail();
scanf("%s",s);
printf("%d",count(s));
return 0;
}
/********************************************************************
ID:Andrew_82
LANG:C++
PROG:Aho-Corasick automation
********************************************************************/
