各種排序演算法詳解&時間、空間複雜度
阿新 • • 發佈:2019-01-01
排序演算法經過了很長時間的演變,產生了很多種不同的方法。對於初學者來說,對它們進行整理便於理解記憶顯得很重要。每種演算法都有它特定的使用場合,很難通用。因此,我們很有必要對所有常見的排序演算法進行歸納。
排序大的分類可以分為兩種:內排序和外排序。在排序過程中,全部記錄存放在記憶體,則稱為內排序,如果排序過程中需要使用外存,則稱為外排序。下面講的排序都是屬於內排序。
內排序有可以分為以下幾類:
(1)、插入排序:直接插入排序、二分法插入排序、希爾排序。
(2)、選擇排序:直接選擇排序、堆排序。
(3)、交換排序:氣泡排序、快速排序。
(4)、歸併排序
(5)、基數排序
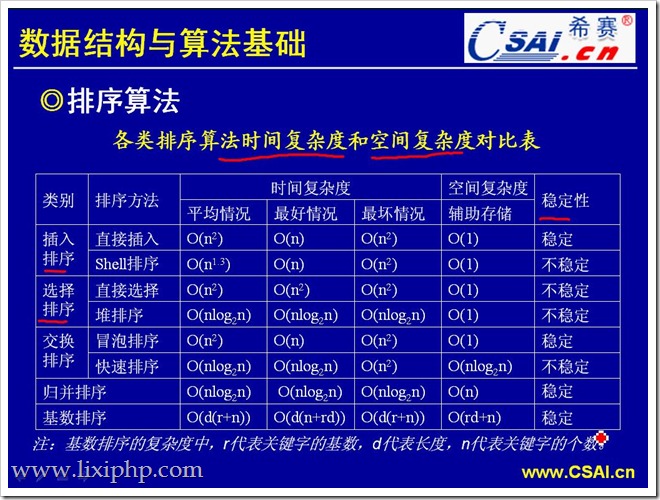
表格版
| 排序方法 | 時間複雜度(平均) | 時間複雜度(最壞) | 時間複雜度(最好) | 空間複雜度 | 穩定性 | 複雜性 |
|---|---|---|---|---|---|---|
| 直接插入排序 | O(n2)O(n2) | O(n2)O(n2) | O(n)O(n) | O(1)O(1) | 穩定 | 簡單 |
| 希爾排序 | O(nlog2n)O(nlog2n) | O(n2)O(n2) | O(n)O(n) | O(1)O(1) | 不穩定 | 較複雜 |
| 直接選擇排序 | O(n2)O(n2) | O(n2)O(n2) | O(n2)O(n2) | O(1)O(1) | 不穩定 | 簡單 |
| 堆排序 | O(nlog2n)O(nlog2n) | O(nlog2n)O(nlog2n) | O(nlog2n)O(nlog2n) | O(1)O(1) | 不穩定 | 較複雜 |
| 氣泡排序 | O(n2)O(n2) | O(n2)O(n2) | O(n)O(n) | O(1)O(1) | 穩定 | 簡單 |
| 快速排序 | O(n | O(n2)O(n2) | O(nlog2n)O(nlog2n) | O(nlog2n)O(nlog2n) | 不穩定 | 較複雜 |
| 歸併排序 | O(nlog2n)O(nlog2n) | O(nlog2n)O(nlog2n) | O(nlog2n)O(nlog2n) | O(n)O(n) | 穩定 | 較複雜 |
| 基數排序 | O(d(n+r))O(d(n+r)) | O(d(n+r))O(d(n+r)) | O(d(n+r))O(d(n+r)) | O(n+r)O(n+r) | 穩定 | 較複雜 |
圖片版
① 插入排序
•思想:每步將一個待排序的記錄,按其順序碼大小插入到前面已經排序的字序列的合適位置,直到全部插入排序完為止。
•關鍵問題:在前面已經排好序的序列中找到合適的插入位置。
•方法:
–直接插入排序
–二分插入排序
–希爾排序
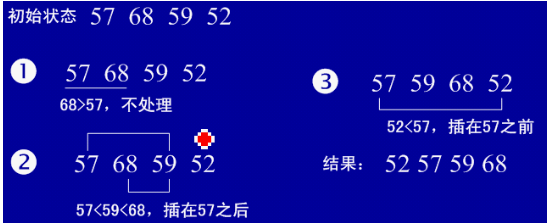
(1)直接插入排序(從後向前找到合適位置後插入)
1、基本思想:每步將一個待排序的記錄,按其順序碼大小插入到前面已經排序的字序列的合適位置(從後向前找到合適位置後),直到全部插入排序完為止。
2、例項
3、java實現
package DirectInsertSort;
public class DirectInsertSort
{
public static void main(String[] args)
{
int[] a = { 49, 38, 65, 97, 76, 13, 27, 49, 78, 34, 12, 64, 1 };
System.out.println("排序之前:");
for (int i = 0; i < a.length; i++)
{
System.out.print(a[i] + " ");
}
// 直接插入排序
for (int i = 1; i < a.length; i++)
{
// 待插入元素
int temp = a[i];
int j;
for (j = i - 1; j >= 0; j--)
{
// 將大於temp的往後移動一位
if (a[j] > temp)
{
a[j + 1] = a[j];
}
else
{
break;
}
}
a[j + 1] = temp;
}
System.out.println();
System.out.println("排序之後:");
for (int i = 0; i < a.length; i++)
{
System.out.print(a[i] + " ");
}
}
}
(2)二分法插入排序(按二分法找到合適位置插入)
1、基本思想:二分法插入排序的思想和直接插入一樣,只是找合適的插入位置的方式不同,這裡是按二分法找到合適的位置,可以減少比較的次