基於PCA和LDA的人臉識別
一、系統設計
1.1研究背景及意義
隨著資訊科技的不斷髮展,人們對方便快捷的身份驗證和識別系統的要求不斷提高。人臉識別技術因具有直接、友好、快捷、方便、易為使用者所接受等特點,成為了身份驗證的最理想依據,也早已成為了模式識別領域研究的熱點。眾多科研人員通過多年潛心研究,也做出了許多的成果,但是在實際應用中,現有的人臉識別產品大多因識別率不高、穩定性差等缺點無法滿足實際需要。
針對這一現狀,本文研究了EigenFace、FisherFace兩種人臉特徵提取演算法,在此基礎上設計了基於PCA+LDA演算法的人臉識別新方案,並對PCA+LDA演算法做了改進。同時還對PCA特徵子空間的維數與識別率的關係進行了研究。
1.2系統開發環境
軟體環境：Windows10
1.3系統使用工具
PyCharm2018.3+Anaconda3+OpenCV
1.4系統功能需求
①人臉檢測：呼叫分類器，將人臉從一張圖片中分析並用適當的框架標識出來
②資料庫儲存：能夠根據情況更新人臉資料庫中的資料，用於訓練；
③人臉識別：能夠根據資料庫中所儲存的人臉資訊，識別出輸入的未知人臉
④動態識別：通過攝像頭的視訊捕捉，能夠實時地識別出每一幀影象中的人臉影象
- 介面設計：需要設計對程式的輸入輸出顯示的功能進行介面的設計
1.5系統資料設計
資料來源：
- yale人臉資料庫：其中共有165張100*100的bmp格式灰度影象，分為15人，每人11張
② 通過呼叫攝像頭自行拍攝的照片，分為2人。每人11張。
2.1EigenFace特徵臉法
EigenFace是基於PCA（主成分分析）的人臉識別演算法。PCA（Principal Component Analysis）是一種常用的資料分析方法。PCA通過線性變換將原始資料變換為一組各維度線性無關的表示，可用於提取資料的主要特徵分量，常用於高維資料的降維。一般情況下，在資料探勘和機器學習中，資料被表示為向量。很多機器學習演算法的複雜度和資料的維數有著密切關係，甚至與維數呈指數級關聯。如果維數較小，也許還無所謂，但是實際機器學習中處理成千上萬甚至幾十萬維的情況也並不罕見，在這種情況下，機器學習的資源消耗是不可接受的，因此我們必須對資料進行降維。
主成分分析（PCA）的原理就是將一個高維向量x，通過一個特殊的特徵向量矩陣U，投影到一個低維的向量空間中，表徵為一個低維向量y，並且僅僅損失了一些次要資訊。也就是說，通過低維表徵的向量和特徵向量矩陣，可以基本重構出所對應的原始高維向量，如圖1。
圖2-1
在人臉識別中，特徵向量矩陣U稱為特徵臉（EigenFace）空間，因此其中的特徵向量ui進行量化後可以看出人臉輪廓。
2.2FisherFace方法
假設有C個人的人臉影象，每個人可以有多張影象，所以按人來分，可以將影象分為C類，這節就是要解決如何判別這C個類的問題。判別之前需要先處理下影象，將每張影象按照逐行逐列的形式獲取畫素組成一個向量，和第一節類似設該向量為x，設向量維數為n，設x為列向量（n行1列）。這裡的n有可能成千上萬，比如100x100的影象得到的向量為10000維，所以第一節裡將x投影到一個向量的方法可能不適用了，比如圖2：
圖2-2
平面內找不到一個合適的向量，能夠將所有的資料投影到這個向量而且不同類間合理的分開，所以我們需要增加投影向量w的個數。
FisherFace是基於線性判別分析（Linear Discriminant Analysis, 以下簡稱LDA）。LDA是一種監督學習的降維技術，也就是說它的資料集的每個樣本是有類別輸出的。這點和PCA不同。PCA是不考慮樣本類別輸出的無監督降維技術。LDA的思想可以用一句話概括，就是“投影后類內方差最小，類間方差最大”。我們要將資料在低維度上進行投影，投影后希望每一種類別資料的投影點儘可能的接近，而不同類別的資料的類別中心之間的距離儘可能的大。
3.1EigenFace實現步驟
(1)獲取包含M張人臉影象的集合dataMat，每張圖轉化為一列，將每一列進行合併，轉為矩陣，最後得到影象矩陣dataMat。
(2)計算平均影象，對行求均值後得到平均臉矩陣MeanMat，若還原回畫素矩陣如圖3-1，並獲得偏差矩陣。每張人臉都減去這個平均影象，最後得到偏差矩陣diffMat。
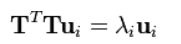
圖3-1求均值後得到的平均臉
(3)求協方差矩陣,並計算特徵值和特徵向量。但是在這裡，協方差矩陣的維度過大，無法計算，計算量大且無法儲存，因此使用如下的方法：
設 T 是預處理影象的矩陣，每一列對應一個減去均值影象之後的影象。則，協方差矩陣為 
，並且對 S 的特徵值分解為
然而，
是一個非常大的矩陣。因此，如果轉而使用如下的特徵值分解
|
|
此時，我們發現如果在等式兩邊乘以T，可得到
|
|
這就意味著，如果 ui 是的一個特徵向量，則
是 S 的一個特徵向量。
這裡的T 就是偏差矩陣，最後我們得
的一個特徵向量，再用T與之相乘就是協方差矩陣的特徵向量u。而此時我們求的特徵向量每一行如果變成影象大小的矩陣，就可以看做是一個新的人臉，稱為特徵臉，如圖4-2。
圖4-2 特徵臉
(4)由於當前問題是小樣本問題，即樣本維數遠遠大於樣本數，而特徵值分解僅適用於方陣，因此這裡我們需要用到與特徵值分解原理相同，但是適用於任意矩陣特徵值的奇異值分解得到協方差矩陣特徵向量。
假設我們的矩陣A是一個m×n的矩陣，那麼我們定義矩陣
A的SVD為：
其中U是一個m×m的矩陣，Σ是一個m×n的矩陣，除了主對角線上的元素以外全為0，主對角線上的每個元素都稱為奇異值，V是一個n×n的矩陣。U和V都是酉矩陣，即滿足UTU=I,VTV=I。
(5)主成分分析。在求得的特徵向量和特徵值中，越大的特徵值對於我們區分越重要，也就是我們說的主成分，我們只需要那些大的特徵值對應的特徵向量，而那些十分小甚至為0的特徵值對於我們來說，對應的特徵向量幾乎沒有意義。在這裡我們選取的特徵向量維數是40維，在大多數應用中，40維已經足夠代表樣本的特徵。
(6) 進行人臉識別。此時我們匯入一個新的人臉，我們使用上面主成分分析後得到的特徵向量
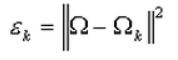
3.2FisherFace實現步驟
(1)與PCA類似，得到訓練集dataMat及需要降至的維度d(d=classNum-1)，減去均值，得到偏差矩陣。
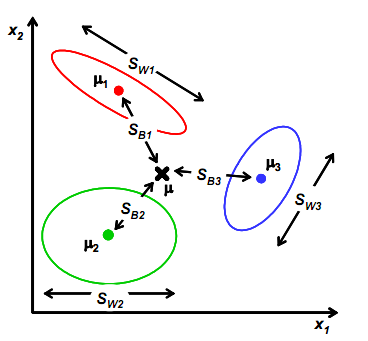
(2)計算類內散度矩陣Sw，Sw定義如下：
其中，
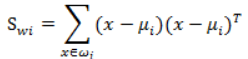
代表類別i的類內雜湊度，它是一個m×n的矩陣。
(3)計算類間散度矩陣SB，SB定義如下：
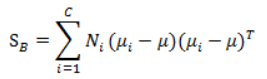
代表每個類別到μ距離的加和，Ni代表類別內i的個數classInnum，也就是某個人的人臉影象個數。
(4)投影方向是多維，求每類中心相對於全樣本中心的雜湊度之和，得到：
最後化為：
同PCA類似，求解矩陣的特徵向量，然後取前d個特徵值最大的特徵向量。
圖4-1
通過PCA降維後的資料不能進行分類，與LDA相比缺少一個獨立標識每個資料的標籤label。做迴歸時，如果特徵太多，會產生不相關特徵引入、過度擬合等問題。如圖4-1左，PCA所做的只是將整組資料整體對映到最方便這組資料的座標軸上，對映時沒有利用任何資料內部的分類資訊。因此，雖然採用了PCA進行降維，整組資料在表示上更加方便（降低了維數並將資訊損失降到最低），但在分類上會變得更加困難。如圖4-1右，在增加了分類之後，兩組輸入對映到了另外一個座標軸上，有了這樣一個對映，兩組資料之間的就變得更易區分了(在低維上就可以區分，減少了很大的運算量)。
但是，在當前實驗中，我們對LDA演算法進行了改進，LDA降維採用的資料集並不是原始的照片，而是PCA降維後的值，原因如下：
(1)通過PCA降維後資料量會明顯減少，提高程式效能。
(2)多重共線性預測變數之間相互關聯，多重共線性空間會導致解空間的不穩定，從而導致結果的不連貫。
(3)高維空間本身具有稀疏性，一維正態分佈有68%的值落於正負標準差之間，而在十維空間上只有0.02%，過多的變數會妨礙查詢規律的建立。
(4)僅在變數層面上分析可能會忽略變數之間的潛在聯絡。例如幾個預測變數可能落入僅反映資料某一方面特徵的一個組內。
共進行了十次測試，每次用十張新的照片與庫中的照片進行比對，最後得到正確率。
5.1EigenFace正確率測試
5.2改進後的FisherFace正確率測試
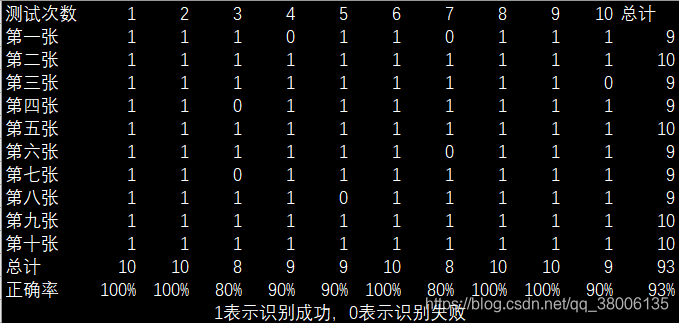
5.3對比及分析
可以明顯看出，改進後的演算法正確率要高得多。
但是由於演算法本身的限制，如果要得到更準確的結果，對樣本的要求較高，光照、人的表情等各個方面都需要考慮，因此我們更換了不同的樣本進行測試，來研究樣本的選取。
當樣本選取正常表情、光照較明亮時，正確率很高；當樣本中人臉表情較浮誇，測試時人的表情正常時，準確率較低。因此，樣本集應該儘量多地包括到人臉的各種表情及考慮到光照，應該儘量光線明亮。
另外，在降維的維數選擇上，我們進行了測試，來判斷對當前應用來說，選取多少維是合適的。
對當前應用來說，維數選取22維已經可以代表特徵，但是為了程式的可擴充套件性，我們還是選取了最佳的40維。
參考文獻
[1]Dan Kalman.A Singularly Valuable Decomposition:The SVD of a Matrix·http://www-users.math.umn.edu/~lerman/math5467/svd.pdf
[2]J.R.Parker.影象處理與計算機視覺演算法及應用(第2版):清華大學出版社，2012
[3]A Tutorial on Principal Component Analysis·https://www.cs.cmu.edu/~elaw/papers/pca.pdf
[4]周志華.機器學習.清華大學出版社，2016
[5]基於PCA和LDA的人臉識別技術的研究.伍威 李晉惠. http://www.docin.com/p-1385093618.html
github地址：https://github.com/Gonlandoo/Face_Recognition
給個星喲