機器學習中，神經網路是如何將線性不可分的樣本，進行很好的分類的？

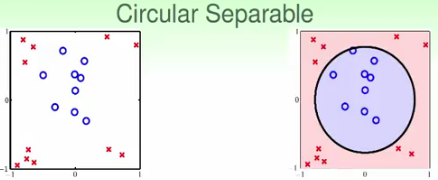
如上圖所示，左圖中的藍色的圓圈和紅色的叉叉是線性不可分的。

如上圖中右圖所示，我們發現它們是可以被一個圓分開的。假設黑色圓圈的公式為： x1^2 + x2^2 + 0.6 = 0，則可以使用如下公式將藍色的圓圈和紅色的叉叉很好的分開。

特徵轉換 :

如上圖所示，我們將x-空間的特徵，轉換為z-空間中的特徵。
在左圖x-空間中，座標的屬性為x1 和 x2,
在右圖z-空間中，座標的屬性為x1的平方和 x2的平方。
經過上述座標變換之後，在右圖中藍色的圓圈和紅色的叉叉就變得線性可分了。
如果我們將我們觀測的屬性進行轉換後

特徵轉換（觀測屬性轉換）的流程：

如上圖所示，我們可以將初始的觀測屬性x（特徵）進行一定的轉換後，使得在新的觀測屬性空間z中我們可以很好的解決我們的問題，（上圖中是找到一條線直線，將圓圈和叉叉進行分開），然後將在新觀測空間中求得的解反向對映到初始的觀測空間中。

神經網路中的每一個隱藏層所做的事情，其實就是將輸入層輸入的觀測屬性 X，進行如上所述的觀測空間的轉換（觀測特徵的轉換），然後使得轉換後的觀測屬性，更便於對我們待解決問題的求解。
所以只要經過足夠多的特徵轉換，求解我們的問題的難度就會越來越簡單。

不過，要進行特徵的轉換，使得更高層的特徵空間可以表示低層特徵空間中的所有情況，是有一定的代價的。