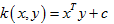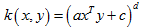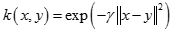機器學習中的特徵變換(核函式)
阿新 • • 發佈：2019-01-09
在機器學習中，我們提供的資料不一定都是完全線性可分的，很多情況下會存線上性不可分，可是我們需要處理成線性可分，所以我們可以採用特徵變換或者核函式的形式，把資料投影到別的空間。資料在A空間不可分，投影到B空間就可能會線性可分，B空間的維度一般會高於A空間的維度。
1.一般情況下，我們考慮將資料投影到別的空間，比如採用多項式。假設x的維度d，如果投影到別的空間，維度會急劇增大，造成維度災難。維度比較高，在求解過程中就會存在問題，比如你在求解SVM的時候，存在不同元素之間的內積，如果投影過去變成10000維，那麼計算內積就要10000次，在繼續增大的話可能導致無法計算。使得計算效率十分低下。很多情況下無法計算。
2.為了解決上面的這個問題，我們採用的思路不是先投影，而是把投影和內積和在一起計算，稱為kernel function（核函式）。計算核函式來替代其他的計算。
以下是幾種常用的核函式表示：
線性核（Linear Kernel）
多項式核（Polynomial Kernel）
徑向基核函式（Radial Basis Function）
也叫高斯核（Gaussian Kernel），因為可以看成如下核函式的領一個種形式：
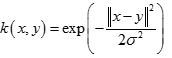徑向基函式是指取值僅僅依賴於特定點距離的實值函式，也就是
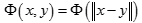。任意一個滿足
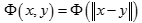特性的函式
Φ都叫做徑向量函式，標準的一般使用歐氏距離，儘管其他距離函式也是可以的。所以另外兩個比較常用的核函式，冪指數核，拉普拉斯核也屬於徑向基核函式。此外不太常用的徑向基核還有ANOVA核，二次有理核，多元二次核，逆多元二次核。冪指數核（Exponential Kernel）
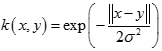拉普拉斯核（Laplacian Kernel）
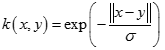ANOVA核（ANOVA Kernel）
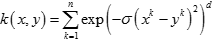二次有理核（Rational Quadratic Kernel）
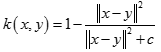多元二次核（Multiquadric Kernel）
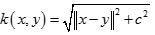逆多元二次核（Inverse Multiquadric Kernel）
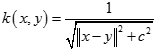另外一個簡單實用的是Sigmoid核（Sigmoid Kernel）
以上幾種是比較常用的，大部分在SVM，SVM-light以及RankSVM中可用引數直接設定。還有其他一些不常用的，如小波核，貝葉斯核，可以需要通過程式碼自己指定。（引用：http://blog.csdn.net/qq_27231343/article/details/51817866）不同kernel function的對比： 線性：簡單，安全，首先嚐試．求解速度快速．線性的好處很容易看出機器如何分類的，並且也知道權重，也可以輕易的計算出支援向量．不過是有限的． 多項式：比線性寬鬆，比線性的限制少，可以解決的問題更多一點，線性沒法解決的這個可以解決．不過計算核函式的值比較難計算，一個數字的ｎ次方會比較難計算，求解二次規劃會有難度．還有就是超引數有點多，比較難選擇．所以這個一般用的時候就是次方比較小的時候． 高斯核函式：就是限制更少，維度是無限維度，可以做出複雜的邊界，數值計算的困難度低一點，超引數只有一個，也稍微簡單點，無法計算出ｗ，需要利用核函式計算結果．求解對偶問題時候比線性慢．引數沒選好會有過擬合的可能性．小心使用，引數選擇小心．