決策樹

import pandas as pd
import numpy as np
import graphviz
from sklearn.tree import DecisionTreeRegressor
from sklearn import tree

X = np.array(data[['C', 'E']])  # Create an array
y = np.array(data['NOx'])

regt = DecisionTreeRegressor(max_depth=4)

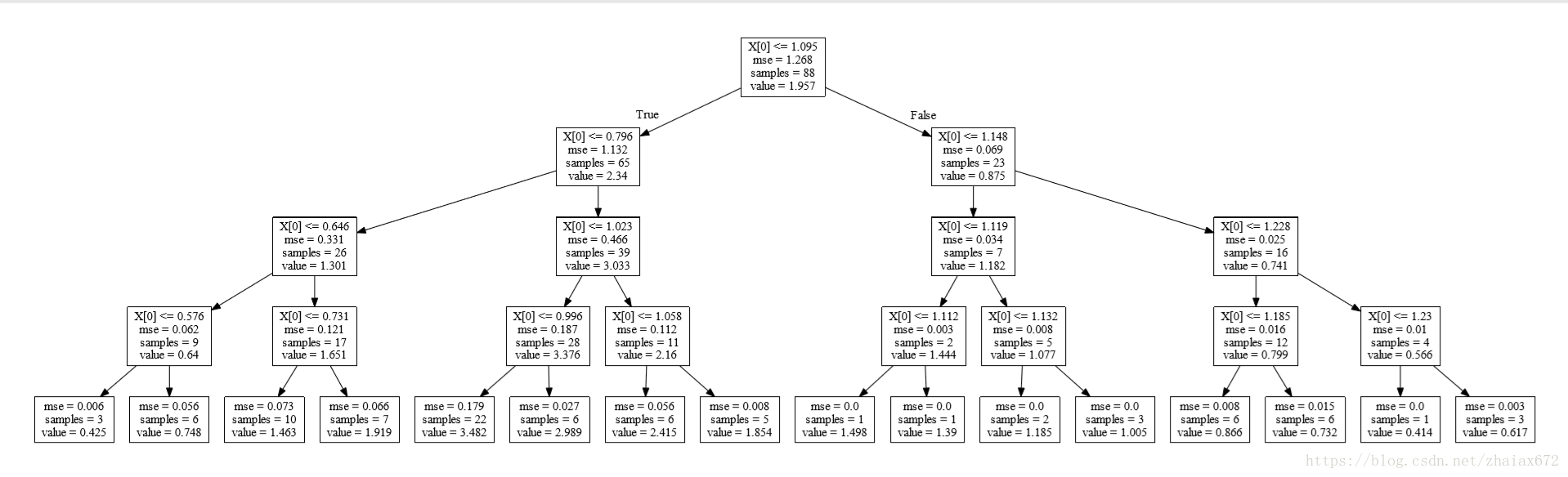
regt = regt.fit(X, y)  # Build a decision tree regressor from the training set (X, y)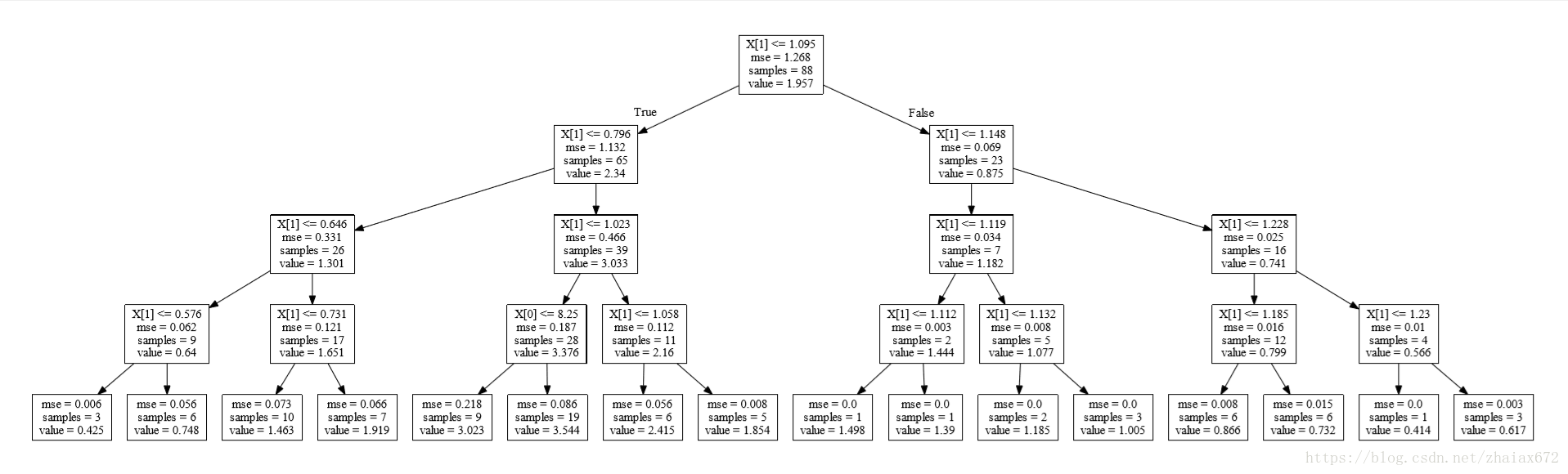
 


dot_data = tree.export_graphviz(regt, out_file=None)  # Export a decision tree in DOT format

graph = graphviz.Source(dot_data)

graph.render("tree")  # Save the source to file

[注]

節點屬性：

• X[1]：X = np.array(data[['C', 'E']])中的E列，為特徵值
• samples：樣本的數量
• mse：均方誤差（mean-square error, MSE）是反映估計量與被估計量之間差異程度的一種
• value：平均值

print(regt.score(X, y))
------------------------------------
0.949306568162

regt1 = regt.fit(X[:, 1].reshape(-1, 1), y)  # reshape(-1, 1) 將陣列改為 多行1列

dot_data = tree.export_graphviz(regt, out_file=None)

graph = graphviz.Source(dot_data)

graph.render("tree1")

regt1.score(X[:, 1].reshape(-1
 
, 1), y)

對比過後，發現 tree 和 tree1 完全相同

u = np.sort(np.unique(X[:, 1]))
t = np.diff(u)/2+u[:-1]  # diff() 後一個元素減去前一個元素

#
mse = []
mse1 = []
mse2 = []
for i in t:
    m1 = (y[X[:, 1] < i]-np.mean(y[X[:, 1] < i]))**2  # X[:, 1] 取該二維陣列第二列所有資料
    m2 = (y[X[:, 1] > i]-np.mean(y[X[:, 1] > i]))**2
    mse1.append(np.mean(m1))  # “拍腦袋”平方和
    mse2.append(np.mean(m2))  # “拍腦袋”平方和
    mse.append((np.sum(m1)+np.sum(m2))/len(y))
I = np.argmin(mse)  # 求mse最小值的index

MSE0 = np.mean((y-np.mean(y))**2)
print("Original total MSE={}\nSplit point={}\nMin mse={}\nLeft mse={}\nRight mse={}".format(MSE0, I, mse[I], mse1[I], mse2[I]))
-------------------------------------------------------------------------------
Original total MSE=1.26845241619
Split point=60
Min mse=0.854108834661
Left mse=1.13202721562
Right mse=0.0686873232514

上述程式碼的函式形式

def spl(X, y):
    u = np.sort(np.unique(X))
    t = np.diff(u)/2+u[:-1]
    mse = []
    mse1 = []
    mse2 = []
    for i in t:
        m1 = (y[X < i]-np.mean(y[X < i]))**2
        m2 = (y[X > i]-np.mean(y[X > i]))**2
        mse1.append(np.mean(m1))
        mse2.append(np.mean(m2))
        mse.append((np.sum(m1)+np.sum(m2))/len(y))
    i = np.argmin(mse)

    return mse[i], t[i], mse1[i], mse2[i]


print(spl(X[:, 1], y))
print(spl(X[:,0], y))
------------------------------------------------------------------
(0.8541088346609912, 1.0945, 1.1320272156213018, 0.06868732325141778)
(1.264189318071551, 13.5, 1.103670472054112, 1.5072607134693878)

def FCV(x, y, regr, cv=10, seed=2015):

    np.random.seed(seed)
    ind = np.arange(len(y))
    np.random.shuffle(ind)  # 隨機化下標

    X_folds = np.array_split(x[ind], cv)
    y_folds = np.array_split(y[ind], cv)

    X2 = np.empty((0, X.shape[1]), float)
    y2 = np.empty((0, y.shape[0]), float)
    yp = np.empty((0, y.shape[0]), float)

    for k in range(cv):
        X_train = list(X_folds)  # 只有list才能pop
        X_test  = X_train.pop(k)  # 從中取出第k份
        X_train = np.concatenate(X_train)  # 合併剩下的cv-1份

        y_train = list(y_folds)
        y_test = y_train.pop(k)
        y_train = np.concatenate(y_train)

        regr.fit(X_train, y_train)  # 擬合選中的regr模型

        y2 = np.append(y2, y_test)
        X2 = np.append(X2, X_test)
        yp = np.append(yp, regr.predict(X_test))

    nmse = np.sum((y2-yp)**2)/np.sum((y2-np.mean(y2))**2)
    r2 = 1-nmse
    return np.array([nmse, r2])

求出 線性迴歸 LinearRegression 和 決策樹 DecisionTreeRegressor 所對應的 NMSE 和 R^2

from sklearn.linear_model import LinearRegression
from sklearn.tree import DecisionTreeRegressor
names = ["Linear Regression", "Decision Tree"]
regressors = [LinearRegression(), DecisionTreeRegressor(max_depth=4)]

A = np.empty((0, 2), float)

for reg in regressors:
    tt = np.array(FCV(X, y, reg, 8))
    tt.shape = (1, 2)  # 一行二列
    A = np.append(A, tt, axis=0)  # 把各種方法的迴歸結果合併

print(A)
-----------------------------------------------------------------
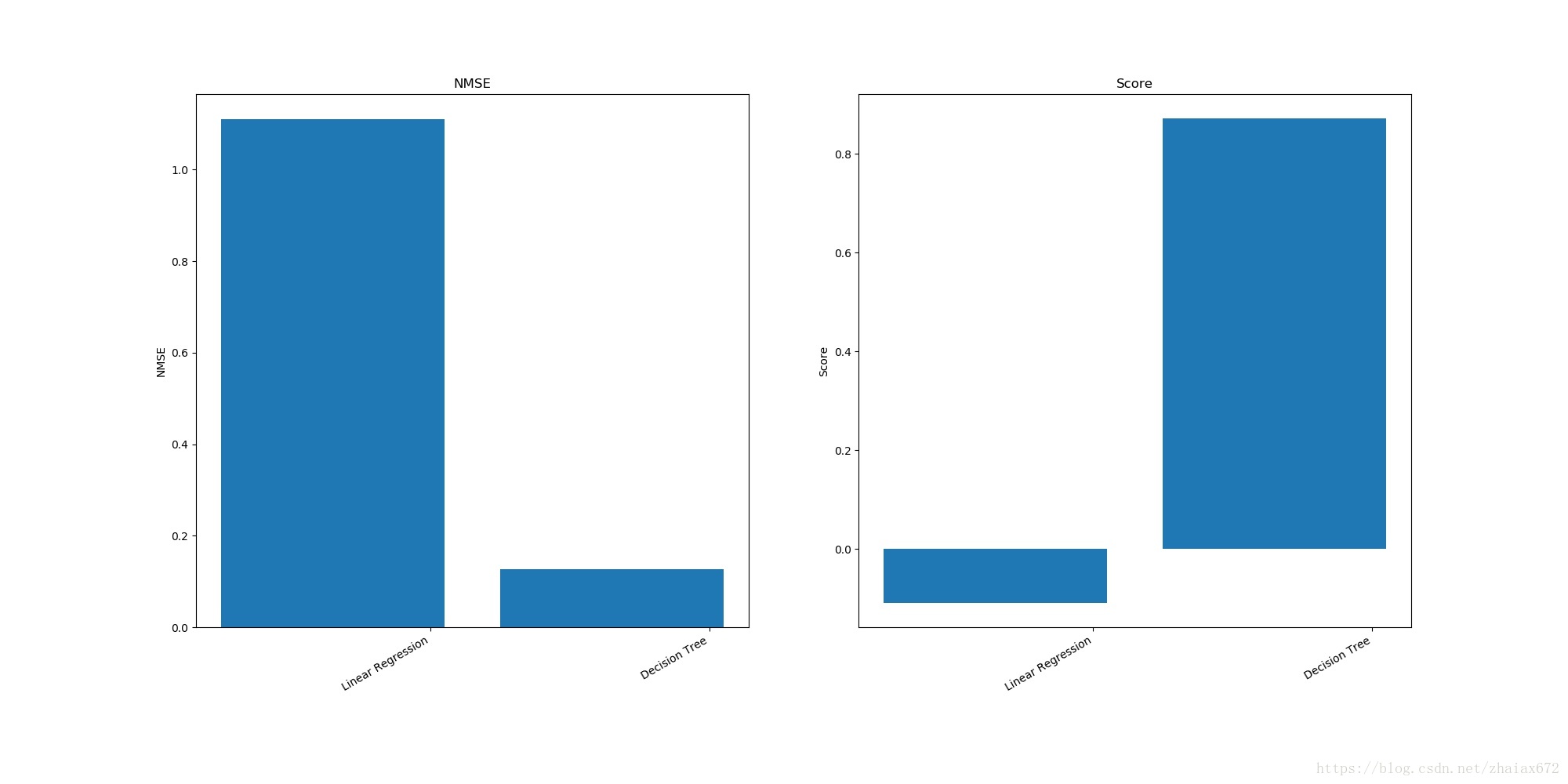
[[ 1.06233633 -0.06233633]
 [ 0.15896376  0.84103624]]

import matplotlib.pyplot as plt

fig = plt.figure(figsize=(20, 10))

ax = fig.add_subplot(121)
ax.bar(np.arange(np.array(A).shape[0]), np.array(A)[:, 0])

ax.set_xticklabels(names)  # 標註迴歸方法
fig.autofmt_xdate()  # 迴歸方法標註斜放

ax.set_ylabel('NMSE')
ax.set_title('NMSE')
ax.set_xticks(np.arange(np.array(A).shape[0]) + 0.35)

bx = fig.add_subplot(122)
bx.bar(np.arange(np.array(A).shape[0]), np.array(A)[:, 1])
bx.set_xticklabels(names)

fig.autofmt_xdate()

bx.set_ylabel('Score')
bx.set_title('Score')
bx.set_xticks(np.arange(np.array(A).shape[0]) + 0.35)

plt.savefig("examples.jpg")

Score：R2$R^2$

bagging 是由 Breiman 提出的一個簡單的組合模型, 它對原始資料集做很多次放回抽樣, 每次抽取和樣本量同樣多的觀測值, 放回抽樣使得每次都有大約百分之三十多的觀測值沒有抽到, 另一些觀測值則會重複抽到, 如此得到很多不同的資料集, 然後對於每個資料集建立一個決策樹, 因此產生大量決策樹. 對於迴歸來說, 一個新的觀測值通過如此多的決策樹得到很多預測值, 最終結果為這些預測值的簡單平均.

from sklearn.ensemble import BaggingRegressor

regr = BaggingRegressor(n_estimators=100, oob_score=True, random_state=1010)
regr.fit(X, y.ravel())

print("Score:", regr.score(X, y))  # Score為可決係數R^2
print("NMSE:", 1-regr.score(X, y))  # 標準化均方誤差 NMSE

Breiman 發明的隨機森林的原理並不複雜, 和 bagging 類似, 它對原始資料集做很多次放回抽樣, 每次抽取和樣本量同樣多的觀測值, 由於是放回抽樣, 每次都有一些觀測值沒有抽到, 一些觀測值會重複抽到, 如此會得到很多不同的資料集, 然後對於每個資料集建立一個決策樹, 因此產生大量決策樹. 和 bagging 不同的是, 在隨機森林每棵樹的每個節點, 拆分變數不是由所有變數競爭, 而是由隨機挑選的少數變數競爭, 而且每棵樹都長到底. 拆分變數候選者的數目限制可以避免由於強勢變數主宰而忽略的資料關係中的細節, 因而大大提高了模型對資料的代表性. 隨機森林的最終結果是所有樹的結果的平均, 也就是說, 一個新的觀測值, 通過許多棵樹(比如 n 棵)得到 n 個預測值, 最終用這 n 個預測值的平均作為最終結果.

from sklearn.ensemble import RandomForestRegressor
from sklearn.datasets import make_regression

regr = RandomForestRegressor(n_estimators=500, oob_score=True, random_state=1010)
regr.fit(X, y.ravel())
print("Variable importance:\n", regr.feature_importances_)
print("Score:\n", regr.oob_score_)
---------------------------------------------------------------------]
('Variable importance:\n', array([0.03731845, 0.00096088, 0.00580794, 0.00074913, 0.02247829,
       0.43575755, 0.01257118, 0.06612205, 0.00307613, 0.01341358,
       0.01549635, 0.0116068 , 0.37464165]))
('Score:\n', 0.8829155069608635)

  <font color=red >問題：score 代表的是 可決係數R^2 嗎？</font>