他講了監督學習的兩類問題，分類和迴歸，並引入了兩個例子。一個講用現有的房屋面積和房價的資料集推算任意房子的價格（可認為是連續的），然後再引入其他模型引數，比如臥室個數等。另一個講用腫瘤的大小來推斷是否為良性或惡性腫瘤，如果引入其他引數，比如腫瘤細胞大小的一致性，及細胞形狀的一致性等，依然可以找出這種關係，其結果是離散的（在其他問題中，可能分多於兩個類，但依然是離散結果，是分類問題）。總之，兩類問題都是根據已知的資料（引數值和輸出）來推算尚未知輸入的輸出，這也就是監督學習的直觀理解。

設計不同的模型來研究現實世界中的問題，引入更多的引數讓該模型更趨近真實情形，這可能就是工程師看世界的角度吧。有人做過北京租房價格的統計，

->戳post，可以在這個基礎上學習一個房價模型（應該鏈家、麥田早就有他們的定價模型吧），現實情況往往復雜很多，鏈家員工去挨家挨戶統計真實住房資訊得磨斷多少腿？->戳video

Cost Function

J(θ)=12m∑im(hθ(xi)−yi)2
h(θ)是要學習的模型，xi為輸入資料，yi是第i個觀測資料，m為資料總量。θ是引數，這個是要學習的結果。學習過程就是不斷調整引數，以使其誤差J(θ)最小。這是跟最小二乘法如出一轍，最小二乘是要誤差為 0。
線上性問題中，模型是這樣表示的，n為引數個數，x下標的意義是第j個輸入變數。
h(θ)=∑jnθjx(j)=θTx

在調整引數的時候，介紹了梯度下降的方法。求偏導部分讀者自行推導一下。

Gradient Descent

θ′j=θj−α∂∂θjJ(θ)=θj−αm∑im((hθ(xi)−yi)xi,(j))
這裡 α 就是學習速率（learning rate），通過給 J 求偏導乘以學習速率來更新引數θ，這樣才會逐漸趨近 J 的區域性最小值 (local minimum)。在視訊裡，他舉了單個引數的例子，在這樣調整的時候，α 並不需用改變，因為每次的步長（Δθ） 是自動減少的，因為它每次在找偏導會變小的方向。如果開始就步長過長，可能第一次調整就越過（overshoot）區域性最小值。xi,(j

)就是第j個變數的第i個輸入。
有兩個變數的時候，J(θ0,θ1) 有直觀的三維平面表示，如下圖。

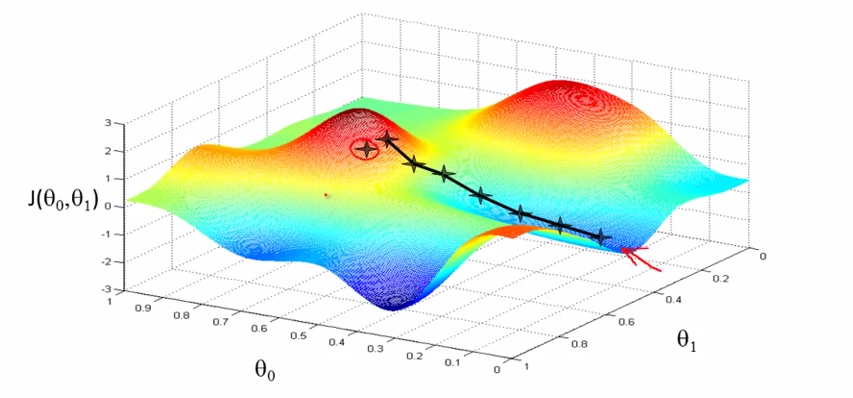
圖中的每個十字是一次迭代計算。每一次迭代的時候好比從該十字向周圍嗅探，去哪兒會降低 J。運氣好的話，會找到波谷（深藍色區域），從不同的出發點開始，可能會去到不同的波谷，運氣差的話，可能走到兩個波峰之間的平地（稱作鞍面，即兩個紅色山丘的中間）。

Vectorized Implementation

線性迴歸的成本函式向量化表達為下式：

Hθ(x)=θx
故，
θ′=θ−α∂∂θJ(θ)=θ−αm∑im((Hθ(x)−y)x)

References