編譯 | AI科技大本營

參與 | 王珂凝

編輯 | 明 明

【AI科技大本營導讀】現在，不管想解決什麼型別的機器學習（ML）問題，都會有各種不同的演算法可以供你選擇。儘管在一定程度上，一種演算法並不能總是優於另外一種演算法，但是可以將每種演算法的一些特性作為快速選擇最佳演算法和調整超引數的準則。

本文，我們將展示幾個著名的用於解決迴歸問題的機器學習演算法，並根據它們的優缺點設定何時使用這一準則。尤其在為迴歸問題選擇最佳機器學習演算法上，本文將會為你提供一個重要的引導！

▌線性迴歸和多項式迴歸

線性迴歸

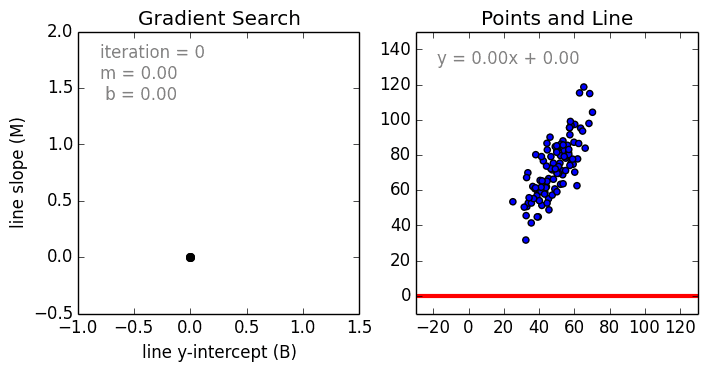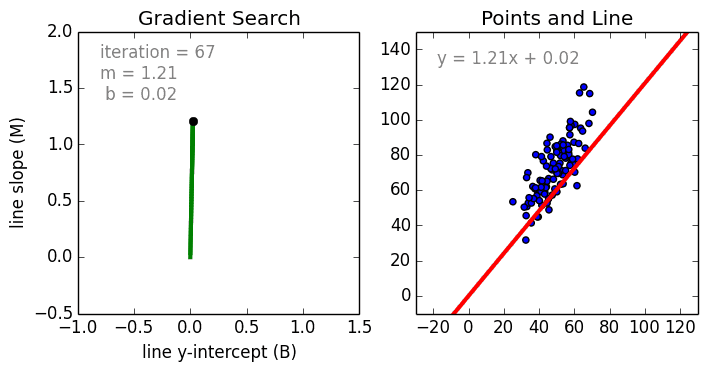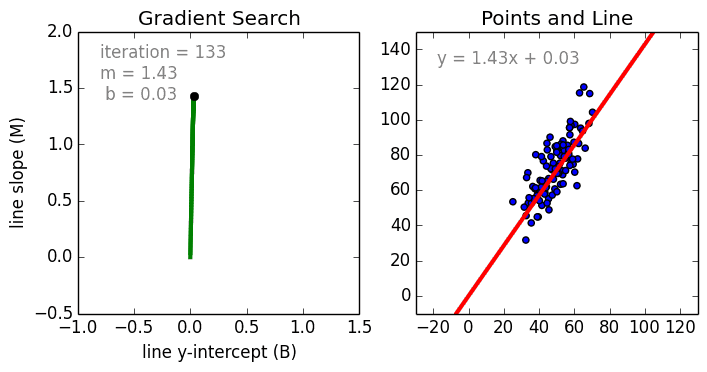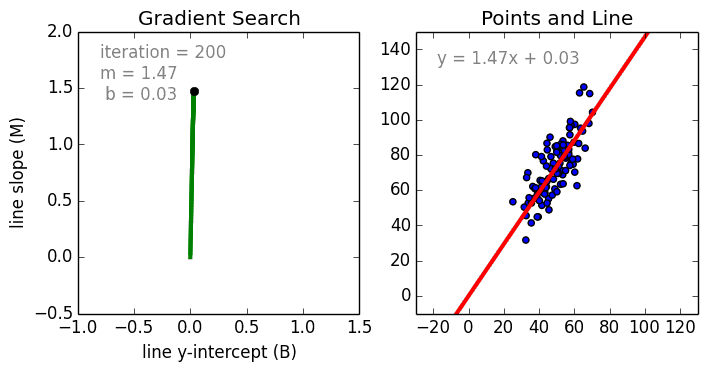
從簡單的情況開始，單變數線性迴歸使用線性模型為單個輸入自變數（特徵變數）和輸出因變數建立關係模型。更為一般的情況是多變數線性迴歸，它為多個獨立的輸入自變數（特徵變數）與輸出因變數之間建立關係模型，該模型始終為線性，這是因為輸出變數是輸入變數的線性組合。

第三種最常見的情況是多項式迴歸，該模型是特徵變數的非線性組合，例如：指數變數，正弦和餘弦等。然而，這需要了解資料是如何與輸出相關的。我們可以使用隨機梯度下降（SGD）對迴歸模型進行訓練。

優點

• 可以快速建模，特別適用於所要建模的關係不是特別複雜並且資料量不大。

• 線性迴歸簡單且易於理解，有利於商業決策。

缺點

• 對於非線性資料進行多項式迴歸設計可能比較困難，因為必須具有特徵變數之間關係和資料結構的一些資訊。

• 由於上述原因，當涉及到資料複雜度較高時，這些模型的效能不如其他模型。

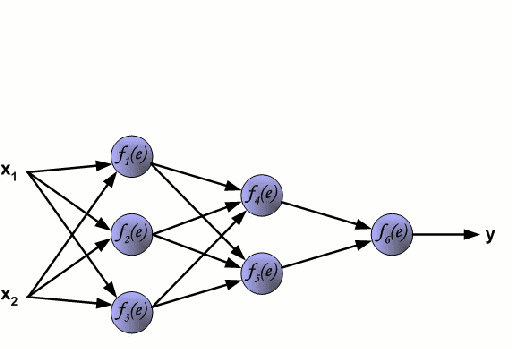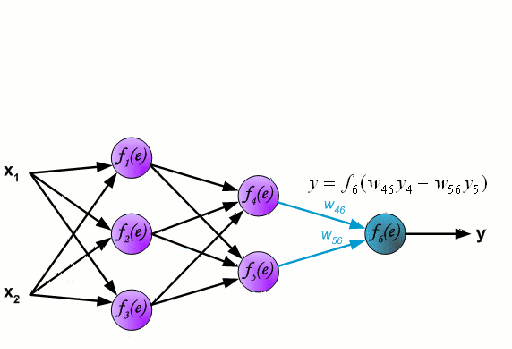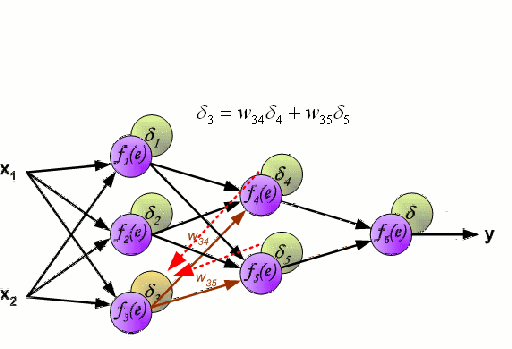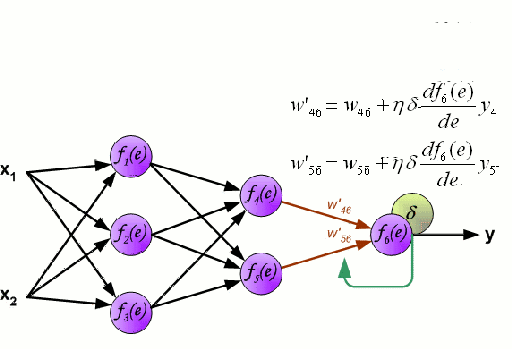
▌神經網絡

神經網路

神經網路是由一組相互連線的節點組成，這些節點被稱為神經元。資料中的輸入特徵變數作為多變數線性組合被傳遞給這些神經元，其中乘以每個特徵變數的值被稱為權重。然後將非線性應用於該線性組合，從而為神經網路對複雜的非線性關係進行建模。神經網路可以有多個層，其中每一層的輸出傳遞給下一層的方式都是相同的。輸出端通常不會使用非線性。我們可以使用隨機梯度下降（SGD）和反向傳播演算法對神經網路進行訓練，這兩種演算法均顯示在上面的動態GIF圖中。

優點

• 由於神經網路可以有多個非線性的層（和引數），因此對非常適合對比較複雜的非線性關係建模。

• 神經網路中的資料結構基本上對學習任何型別的特徵變數關係都非常靈活。

• 研究表明，為網路提供更多的訓練資料（不管是增加全新的資料集還是對原始資料集進行擴張）可以提高網路效能。

• 設定也有利於提高網路效能。

缺點

• 這些模型較複雜，因此不太容易被理解。

• 網路的訓練可能非常具有挑戰性和計算密集性，需要對超引數進行微調並設定學習率表。

• 網路的高效能需要大量的資料來實現，在“少量資料”情況下通常不如其他機器學習演算法的效能。

▌迴歸樹和隨機森林

隨機森林

決策樹是一種直觀的模型，它通過遍歷樹的分支並根據節點的決策選擇下一個分支進行遍歷。決策樹歸納法（Decision Tree Induction）將一組訓練例項作為輸入，確定哪些屬性最適合分割，並對資料集進行分割，在分割後的資料集上進行迴圈，直到對所有訓練例項都被分類為止，任務結束。

構建決策樹旨在分割可能建立純度子節點的屬性，這將會盡可能的減少對資料集中的所有例項進行分類所需要的分割次數。純度是通過資訊增益來衡量的，這涉及到為了進行正確的分類而需要知道有多少以前沒有的例項。在實際應用中，這通過比較熵或者將當前資料集分割槽的單個例項分類所需的資訊的量來衡量，即若當前的資料集分割槽在給定的屬性上被進一步劃分的話，就可以對單個例項進行分類。

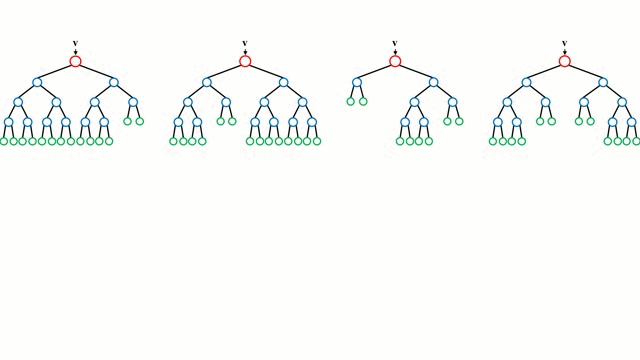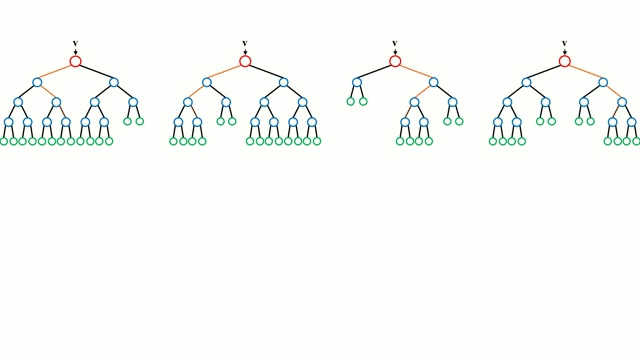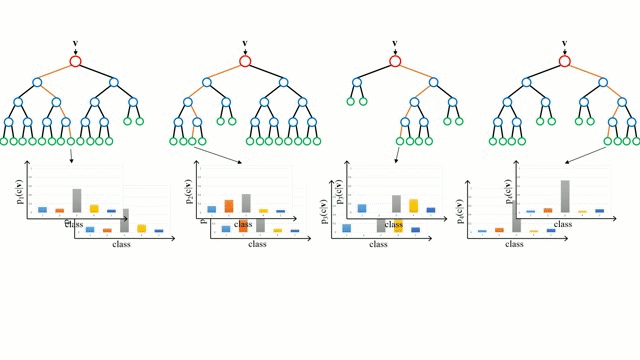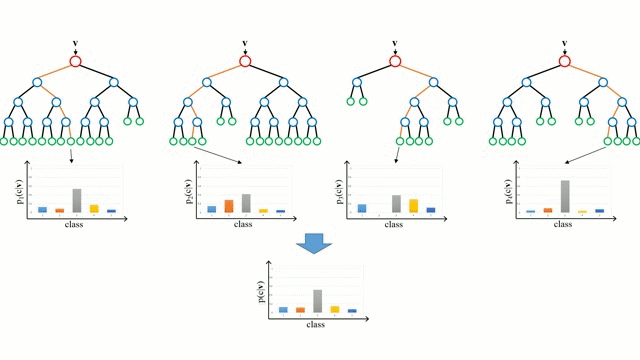
隨機森林是一個簡單的決策樹的集合，輸入向量在多個決策樹上執行。對於迴歸問題，所有決策樹的輸出值都是平均的；對於分類問題，使用一個投票方案來確定最終的類別。

優點：

• 善於學習複雜且高度非線性的關係，通常可以具有很高的效能，其效能優於多項式迴歸，並且通常與神經網路的效能相當。

• 非常便於理解，雖然最終的訓練模型可以學習較為複雜的關係，但是在訓練過程中建立的決策邊界很容易理解。

缺點：

• 由於訓練決策樹的性質，可能很容易出現重大的過度配合。完整的決策樹模型可能過於複雜並且包含不必要的結構。有時可以通過適當的樹木修剪和較大的隨機森林合奏來緩解這種情況。

• 使用較大的隨機森林合奏來獲得更高的效能，會使速度變慢，並且需要更多的記憶體。

▌結語

機器學習中有一種定理叫做“沒有免費的午餐”：並不存在一個能夠解決所有問題的機器學習演算法。機器學習演算法的效能在很大程度上依賴於資料大小和資料結構。因此，我們可以通過簡單的實驗和判斷來測試所選擇是否為最佳演算法。

作者：George Seif

原文網址