被錘爆了

被這個題搞得自閉了一上午，覺得自己沒什麽前途了

我又沒有看出來這個題的一個非常重要的性質

我們填進去的數一定是單調不降的

首先如果填進去的數並不是單調不降的，那麽填進去本身就會產生一些逆序對，感性理解好像是單調不降更優，這裏還是嚴謹證明一下吧

考慮一下樹狀數組求逆序對的過程，顯然就是求出每一個數前面有多少個比它大的數

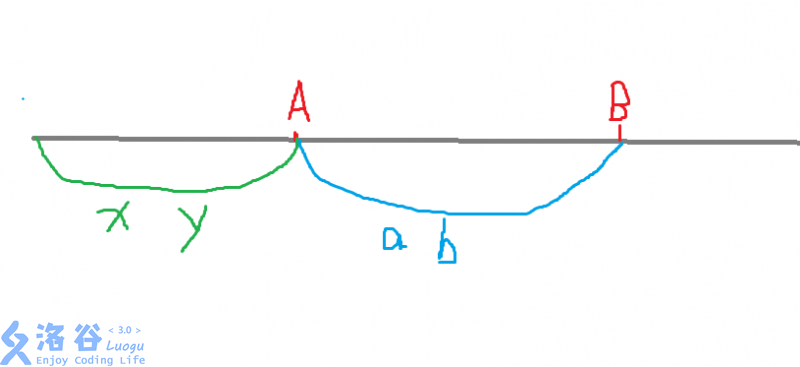
這張圖好醜啊

設\(A<B\)，\(x\)表示那段綠色區間裏大於\(A\)的數，\(y\)表示綠色區間裏大於\(B\)的數，\(a\)表示藍色區間裏大於\(A\)的數，\(b\)表示藍色區間裏大於\(B\)的數

這個時候我們如果用樹狀數組來統計一下答案的話，\(A,B\)

如果交換一下\(A\)和\(B\)的位置，那麽這個時候答案就會變成\(x+a+y+1\)

非常顯然的是\(b<=a\)，所以可以得出\(x+y+b<x+a+y+1\)，所以不交換更優

之後有了這個性質，我們就可以做一個\(dp\)了，設\(dp[i][j]\)表示填到了\(i\)位置，最靠後的一個\(-1\)位置填了\(j\)這個時候的最小逆序對是多少

就可以一邊樹狀數組一邊\(dp\)了

復雜度\(O(nklogk)\)

代碼

#include<iostream>
#include<cstring>
#include<cstdio>
#define LL long long
#define lowbit(x) ((x)&(-x))
#define re register
#define maxn 100005
#define min(a,b) ((a)<(b)?(a):(b))
inline int read()
{
    char c=getchar();
    int x=0,r=1;
    while(c<‘0‘||c>‘9‘) 
    {
        if(c==‘-‘) r=-1;
        c=getchar();
    }
    while(c>=‘0‘&&c<=‘9‘)
        x=(x<<3)+(x<<1)+c-48,c=getchar();
    return x*r;
}
LL c[105];
int n,m;
LL ans;
LL dp[maxn][101];
LL mx[101];
int pre[maxn];
int a[maxn];
int beh[maxn][101];
inline void add(int x)
{
    for(re int i=x;i<=m;i+=lowbit(i)) c[i]++;
}
inline LL ask(int x)
{
    LL now=0;
    for(re int i=x;i;i-=lowbit(i)) now+=c[i];
    return now;
}
int main()
{
    int cnt=0;
    n=read(),m=read();
    for(re int i=1;i<=n;i++) 
    {
        a[i]=read();
        if(a[i]==-1&&!cnt) cnt=i;
        pre[i]=pre[i-1]+(a[i]==-1);
    }
    if(!cnt) cnt=n+1;
    for(re int i=1;i<cnt;i++)
    {
        ans+=ask(m)-ask(a[i]);
        add(a[i]);
    }
    if(cnt==n+1)
    {
        std::cout<<ans;
        return 0;
    }
    for(re int i=n;i;i--)
    {
        for(re int j=1;j<=m;j++)
            beh[i][j]=beh[i+1][j];
        if(a[i]==-1) continue;
        for(re int j=a[i];j<=m;j++) beh[i][j]++;
    }
    memset(dp,20,sizeof(dp));
    for(re int i=1;i<=m;i++)
        dp[cnt][i]=ans+ask(m)-ask(i)+beh[cnt][i-1];
    memset(mx,20,sizeof(mx));
    for(re int j=1;j<=m;j++)
        mx[j]=min(mx[j-1],dp[cnt][j]);
    for(re int i=cnt+1;i<=n;i++)
    {
        if(a[i]!=-1)
        {
            LL now=ask(m)-ask(a[i]);
            for(re int j=1;j<=m;j++)
                dp[i][j]=now+dp[i-1][j];
            add(a[i]);
        }
        else
        {
            for(re int j=1;j<=m;j++)
            {
                LL now=ask(m)-ask(j);
                dp[i][j]=mx[j]+now+beh[i][j-1];
            }
        }
        memset(mx,20,sizeof(mx));
        for(re int j=1;j<=m;j++)
            mx[j]=min(mx[j-1],dp[i][j]);
    }
    LL Ans=0x7ffffffff;
    for(re int i=1;i<=m;i++)
        Ans=min(Ans,dp[n][i]);
    std::cout<<Ans;
    return 0;
}   
 

【[AHOI2008]逆序對】