演算法介紹(3) 編輯距離演算法-字串相似度
編輯距離,又稱Levenshtein距離,是指兩個字串之間,由一個轉成另一個所需的最少編輯操作次數。
具體的操作方法為:
1.修改一個字元(如把“a”替換為“b”)。
2.增加一個字元(如把“abdd”變為“aebdd”)。
3.刪除一個字元(如把“travelling”變為“traveling”)。
具體演算法過程可按一下步驟進行:
設 L(i,j)為使兩個字串和Ai和Bj相等的最小操作次數。
當ai==bj時 顯然 L(i,j) = L(i-1,j-1)
當ai!=bj時
若將它們修改為相等,則對兩個字串至少還要操作L(i-1,j-1)次
若刪除ai或在bj後新增ai,則對兩個字串至少還要操作L(i-1,j)次
若刪除bj或在ai後新增bj,則對兩個字串至少還要操作L(i,j-1)次
此時L(i,j) = min( L(i-1,j-1), L(i-1,j), L(i,j-1) ) + 1
顯然,L(i,0)=i,L(0,j)=j, 再利用上述的遞推公式,可以直接計算出L(i,j)值。
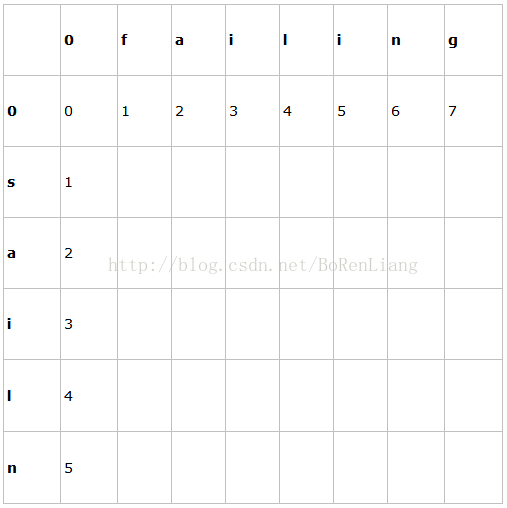
構造編輯距離矩陣如下:
由於L(i,0)=i,L(0,j)=j,所以有:
計算L(1, 1),L(0, 1) + 1 == 2,L(1, 0) + 1 == 2,L(0, 0) == 0 ,min(L(0, 1),L(1, 0),L(0, 0) ) + 1
最後得矩陣如下:
public class MinimumEditDistanceUtil {
public static double MinimumDistance(String sourceStr, String targetString)
{
int sourceLength = sourceStr.length();
int targetLength = targetString.length();
sourceStr = sourceStr.toLowerCase();
targetString = targetString.toLowerCase();
int editMatrix[ ][ ] = new int[sourceLength][targetLength];
for(int i = 0; i < sourceLength; i++)
editMatrix[i][0] = i;
for(int j = 0; j < targetLength; j++)
editMatrix[0][j] = j;
editMatrix[0][0] = 0;
for(int i = 1; i < sourceLength; i++)
{
for(int j = 1; j < targetLength; j++)
{
if(sourceStr.charAt(i - 1) == targetString.charAt(j - 1))
editMatrix[i][j] = editMatrix[i - 1][j - 1];
else
editMatrix[i][j] = minimumValue(editMatrix[i][j - 1], editMatrix[i - 1][j], editMatrix[i - 1][j - 1]) + 1;
}
}
return editMatrix[sourceLength - 1][targetLength - 1];
}
public static int minimumValue(int a, int b, int c)
{
int t = a <= b? a : b;
return t <= c? t : c;
}
public static double stringSimilarity(String sourceStr, String targetString)
{
return 1 - MinimumDistance(sourceStr, targetString) / Math.max(1, sourceStr.length() + targetString.length());
// return 1 - MinimumDistance(sourceStr, targetString) / Math.max(sourceStr.length(), targetString.length());
}
}